Графические методы обработки результатов

 

Очень важным методом обработки результатов опыта является представление их в виде графика. В экспериментальных исследованиях графиками пользуются, прежде всего, для наглядности.

Пример 1. Допустим, что мы изучаем опытным путем, как зависит скорость течения воды в трубке от перепада давления на ее концах. Цель изучения — выяснить, когда поток перестает быть ламинарным (без перемешивания слоев и завихрений) и становится турбулентным (течение сопровождается завихрениями и перемешиванием слоев). Полученные опытные данные приведены в табл. 2.

Таблица 2

Перепад давления, Па/м	Скорость, мм/с	Перепад давления, Па/м	Скорость, мм/с
7,8		78,3	245
15,6		86,0
23,4		87,6
31,3		93,9
39,0		101,6
46,9		109,6
54,7		118,0
62,6

 

Известно, что пока поток остается ламинарным, скорость его пропорциональна перепаду давления. Однако из чисел, приведенных в табл. 2, не видно, где пропорциональность начинает нарушаться. Иное дело, когда те же данные представлены графически (рис. 1.6). В этом случае сразу видна точка А, в которой нарушается пропорциональность.

 

Рис 1.6

 

Пример 2. На рис. 1.7 изображен теоретический график (по теории Дебая) зависимости теплоемкости одного киломоля вещества (в относительных единицах) от температуры (в относительных единицах) и нанесены экспериментальные точки для четырех веществ. График наглядно показывает, что: а) с повышением температуры указанные вещества «ведут себя» одинаково; б) полученные экспериментальные данные подтверждают правильность теоретической кривой.

 

Рис. 1.7

 

Графики используют, чтобы установить эмпирические (на основе опытных данных) зависимости между двумя физическими величинами. Графики позволяют получать количественную информацию о физических процессах, особенно когда графиком является прямая.

Как строить графики

 

Графики можно строить по ходу эксперимента или после его окончания, вручную или используя ЭВМ (с графопостроителем или без него). Но прежде необходимо изобразить координатные оси, выбрать единицы физических величин и масштаб.

В физике принято при построении графиков откладывать по горизонтальной оси независимую переменную, т. е. величину, значения которой задает сам экспериментатор (причина), а по вертикальной оси — ту величину, которую он при этом определяет (следствие).

В любом случае графики — и экспериментальные и теоретические — строят по точкам. На рис. 1.8 а показано, как надо строить линию графика по экспериментальным точкам. Во-первых, линия графика должна быть плавной и, во-вторых, количество точек над и под ней должно быть приблизительно одинаковым. При этом точки, лежащие далеко от графика, не должны учитываться, их следует перепроверять (такие точки называют выбросами). На рис. 1.8 б показано, как нельзя строить графики поэкспериментальным точкам.

Рис 1.8

 

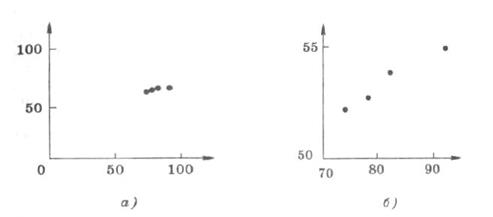
Соединять точки ломаной линией исчитать ее графиком нельзя, так как это означало бы, что при изменении одной величины другая изменяется резкими скачками, что мало вероятно; более вероятно, что зависимость плавная.

Графики должны быть предельно ясными. Этому способствует удачный выбор масштаба. На рис. 1.9 а показан неудачный выбор масштаба для графического представления результатов, на рис. 1.9 б — те же данные в увеличенном масштабе.

 

Рис. 1.9

 

Как и когда указывать погрешности на графике

Погрешность в экспериментальном измерении физической величины можно указать так, как показано на рис. 1.10.

Рис. 1.10

 

Поскольку нанесение таких знаков дополнительный труд и приводит к усложнению графика, это следует делать лишь тогда, когда информация о погрешностях действительно нужна. Так, снабдив соответствующей погрешностью каждую точку на рис. 1.7 мы мало что добавили бы этим к пониманию характера зависимости.

Иное дело, когда от погрешностей может зависеть значимость отклонения экспериментальных данных от теоретической кривой; в этом случае погрешности необходимо указывать. Так, для экспериментальных точек на рис. 1.11 а отклонение результата от теории можно не считать значимым, а на рис. 1.11 6 оно значимо. Погрешности указывают также, если они неодинаковы для разных экспериментальных точек.

 

Рис 1.11

 

Функциональные масштабы

 

В ряде случаев бывает заранее известен вид математической функции, выражающей исследуемую зависимость между физическими величинами. Такая зависимость может быть линейной (зависимость между деформацией пружины и растягивающей ее силой), квадратичной (зависимость от времени расстояния, пройденного телом при падении), показательной (зависимость сопротивления полупроводника от температуры) и т. д. На графиках такие зависимости изображаются известными геометрическими линиями: прямой, параболой, экспонентой и т. д. Однако пользуясь экспериментальными данными, можно с достаточной степенью достоверности построить лишь прямую. Проводя же плавную кривую между экспериментальными точками, нельзя поручиться, что получилась часть параболы, экспоненты или какой-либо другой линии.

В таких случаях при построении графика целесообразно откладывать на координатных осях (или одной из них) не сами величины, между которыми определяется зависимость, а некоторые функции этих величин. Надлежащим выбором вида этих функций можно добиться, чтобы точки графика определяли прямую линию. Например, при изучении свободного падения тела предполагается, что результаты должны описываться законом

 

 

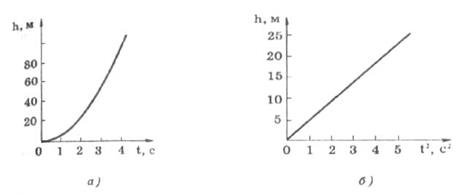
где h — расстояние, пройденное телом за время t; g — ускорение свободного падения. Если по осям откладывать h и t, то точки графика должны определять параболу (рис. 1.12а). Если же по осям откладывать соответственно h и t², то графиком является прямая, проходящая через начало координат (рис. 1.12 б). Измерив угол наклона прямой, можно оценить значение ускорения свободного падения.

 

Рис. 1.12

 

Однако возможны такие функциональные зависимости, когда для исследуемой величины лучше применить логарифмический масштаб. Это необходимо, если исследуемая величина в рассматриваемых пределах изменения аргумента изменяется очень сильно (на несколько порядков, т. е. в сотни, тысячи, миллионы раз). Логарифмический масштаб позволяет весь график поместить на одном чертеже.

Если вид математической функции, описывающей исследуемую зависимость, заранее неизвестен, то строят графики этой зависимости в различных функциональных масштабах; при этом можно найти такой из них, что график будет иметь вид прямой. В результате появляется возможность подобрать к исследуемой зависимости описывающую ее математическую функцию.

 

 

Оформление отчета о проделанной работе

 

Условно лабораторные работы можно разделить на измерительные и наблюдательные. Для каждого вида работ предлагаются единые формы отчета, приводимые ниже.

 

Измерительная лабораторная работа:

1) номер работы;

2) наименование работы;

3) цель работы;

4) чертеж (если требуется);

5) формулы для определения искомых величин и их погрешностей;

6) таблица с результатами измерений и вычислений;

7) окончательный результат, вывод и пр. (согласно цели работы).

 

Наблюдательная лабораторная работа:

1) номер работы;

2) наименование работы;

3) номер опыта;

4) цель опыта;

5) методика проведения опыта;

6) результаты наблюдения;

7) вывод;

8) общий вывод о проделанной работе (если требуется).

 

 

Лабораторная работа № 1