Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерения и погрешности измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Физика как наука родилась более 300 лет назад, когда Галилео Галилей по сути создал научный метод изучения физических явлений, познания физических законов: физические законы устанавливаются и проверяются экспериментально путем накопления и сопоставления опытных данных, обычно представляемых некоторым набором чисел; формулируются законы языком математики, т. е. с помощью формул, связывающих функциональной зависимостью числовые значения физических величин. Именно в этом смысле следует понимать утверждения: физика – наука экспериментальная, физика – наука количественная. Выполняя лабораторные работы, учащиеся, во-первых, изучают на опыте физические явления, воспроизводя их самостоятельно, во-вторых, учатся правильно анализировать результаты опыта и, в-третьих, учатся правильно измерять числовые значения физических величин и сопоставлять их с вычисленными по формулам. Познакомимся, прежде всего, с некоторыми характерными особенностями любых измерений. Измерение — это нахождение числового значения физической величины опытным путем с помощью средств измерений. Примерами средств измерений могут служить линейка, транспортир, весы, динамометр, барометр, часы, амперметр, вольтметр и др. Измерения могут быть прямыми и косвенными. Прямое измерение – это нахождение числового значения физической величины непосредственно средствами измерения. Например, длину стола определяют измерительной лентой, атмосферное давление — барометром, напряжение — вольтметром. Косвенное измерение – это нахождение числового значения физической величины по формуле, связывающей искомую величину с другими физическими величинами, определяемыми прямыми измерениями. Например, числовое значение сопротивления R проводника определяют по формуле Рассмотрим некоторые примеры измерений. Пример 1. Рисунок 1.1 иллюстрирует измерение длины L бруска миллиметровой линейкой (цена деления линейки 1 мм).
Рис 1.1
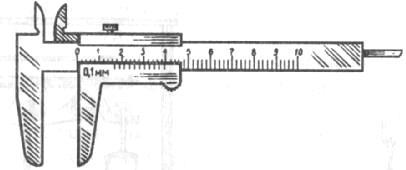
Риска с отметкой «0» линейки с левым концом бруска. Длину бруска должна показать риска, расположенная у его правого конца. Но такой риски нет. Поэтому можно лишь утверждать, что длина бруска больше 39 мм и меньше 40 мм (39 мм < L < 40 мм), т. е. результат измерения приближенный. Истинная длина L бруска неизвестна. Ширина интервала «неизвестности» составляет 1 мм, т. е. равна цене деления линейки. Поэтому следует ожидать, что замена линейки более чувствительным (с меньшей ценой деления) средством измерения сузит этот интервал. Обычно говорят, что при этом повысится точность измерений или уменьшится погрешность (неточность) измерений (в нашем примере погрешность не превышает 1 мм).
Рис. 1.2
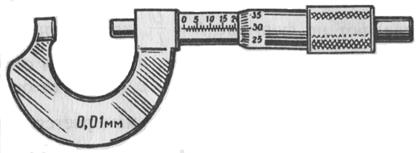
К примеру, длина того же бруска, измеренная штангенциркулем (рис. 1.2) с ценой деления 0,1 мм, оказалась в пределах 39,3 мм < L < 39,4 мм. Погрешность измерения не превышает 0,1 мм. Погрешность стала меньше, но не перестала существовать! Точность измерения длины бруска можно еще более повысить, если использовать микрометр (рис. 1.3), цена деления которого 0,01 мм.
Рис.1.3
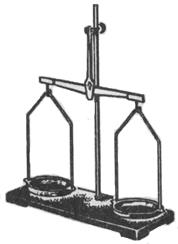
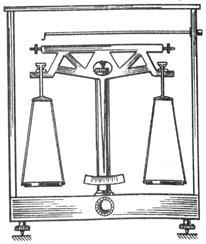
Правда, здесь нас поджидает неожиданность. Результаты повторных измерений не совпадают: 39,34 мм; 39,36; 39,33; 39,35 мм. Причина расхождения результатов измерений — тоже погрешности! Пример 2. Взвешивание двух пластин порознь (т1 и т2)и вместе (т), выполненное на технических весах (рис. 1.4), дало такие результаты: т1 = 21,2 г; т2 = 63,4 г; т = 84,5 г. Различие между т1 + т2 = 84,6 г и т незначительно (0,1 г), но существует. Какова причина? В неправильности утверждения о равенстве этих величин (т = т1 + т2) или наличие погрешностей измерений? Повторим взвешивание на более точных аналитических весах (рис. 1.5): т1 = 21,235 г; т2 = 64,432 г; т = 84,667 г. Расхождение теперь составляет всего 0,006 г, но все же существует.
Рис 1.4 Рис 1.5
Выполнив повторные взвешивания первой пластины на аналитических весах, получим: 21,238; 21,233; 21,237 г. Таким образом, как и в предыдущем примере, при взвешивании всегда имеют место погрешности измерений. По крайней мере, этим можно объяснить расхождения между числовыми значениями т1 + т2 и т. Более того, даже если бы результаты точно совпадали, нельзя быть уверенными в том, что совпадение является истинным, а не представляет собой случайную игру погрешностей.
Подведем итог сказанному. Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный. Всегда имеется некоторая неопределенность в числовом значении измеряемой физической величины. Эта неопределенность характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. Перечислим некоторые из причин, приводящих к появлению погрешностей. 1. Ограниченная точность изготовления средств измерения (например, линейки в большей или в меньшей степени отличаются от эталона, по которому были изготовлены); наличие наименьшего значения измеряемой величины, которое можно получить с помощью данного средства измерения (оно определяется ценой деления шкалы средства измерения). 2. Влияние на измерения неконтролируемых внешних условий (колебание температуры в помещении, непостоянство напряжения в электрической цепи и т. д.). 3. Действия экспериментатора (включение секундомера с запаздыванием, различное положение глаза относительно шкалы измерительного прибора и т. д.). 4. Неполное соответствие измеряемого объекта той модели, которая принята для искомой физической величины. Например, при измерении объема бруска последний принимается за идеальный прямоугольный параллелепипед, в то время как у него имеются закругления на ребрах и вершинах. 5. Приближенный характер законов, которые используются для нахождения измеряемой величины или лежат в основе работы приборов. Перечисленные выше причины появления погрешностей принципиально неустранимы. Часть погрешностей может быть сведена к необходимому минимуму, для другой же части существуют методы их оценки. Такие оценки необходимы как в практической деятельности (например, для подгонки друг к другу деталей какого-либо механизма), так и в науке для установления достоверности выводов, полученных на основании экспериментальных данных.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.179.238 (0.012 с.) |

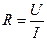 , когда сила тока I в проводнике и напряжение U на его концах измеряются соответственно амперметром и вольтметром; плотность ρ жидкости определяют по формуле
, когда сила тока I в проводнике и напряжение U на его концах измеряются соответственно амперметром и вольтметром; плотность ρ жидкости определяют по формуле 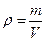 , когда масса жидкости т измеряется взвешиванием на весах, а объем V – мензуркой.
, когда масса жидкости т измеряется взвешиванием на весах, а объем V – мензуркой.