
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация средств измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средства измерений можно классифицировать по двум признакам: 1) по конструктивному исполнению; 2) по метрологическому назначению. По конструктивному исполнению средства измерений классифицируются: 1. Мера физической величины – средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью. Различают следующие разновидности мер: - однозначная мера – мера, воспроизводящая физическую величину одного размера (например, гиря 1 кг); - многозначная мера – мера, воспроизводящая физическую величину разных размеров (например, штриховая мера длины); - набор мер – комплект мер разного размера одной и той же физической величины, предназначенных для применения на практике, как в отдельности, так и в различных сочетаниях (например, набор концевых мер длины); - магазин мер – набор мер, конструктивно объединенных в единое устройство, в котором имеются приспособления для их соединения в различных комбинациях (например, магазин электрических сопротивлений). Часто к однозначным мерам относят стандартные образцы (СО) – образцы вещества (материала) с установленными в результате метрологической аттестации значениями одной или более величин, характеризующими свойство или состав этого вещества (материала). Различают стандартные образцы свойства (относительной диэлектрической проницаемости) и стандартные образцы состава (состава углеродистой стали). Значение величины, приписанное мере или партии мер при изготовлении называется номинальным. 2. Измерительный прибор – средство измерений, предназначенное для получения значений измеряемой физической величины в установленном диапазоне. По способу индикации значений измеряемой величины измерительные приборы разделяют на показывающие и регистрирующие. По действию измерительные приборы разделяют на интегрирующие и суммирующие. Различают также приборы прямого действия и приборы сравнения, аналоговые и цифровые, самопишущие и печатающие приборы 3. Измерительный преобразователь (ИП) – техническое средство с нормативными метрологическими характеристиками, служащее для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи. ИП или входит в состав какого-либо измерительного прибора (измерительной установки, измерительной системы и др.), или применяется вместе с каким-либо средством измерений. По характеру преобразования различают аналоговые, цифро - аналоговые, аналого - цифровые преобразователи. По месту в измерительной цепи различают первичные и промежуточные преобразователи. Выделяют также масштабные и передающие преобразователи. Пример: измерительный трансформатор тока. 4. Измерительная установка – совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей и других устройств, предназначенная для измерений одной или нескольких физических величин и расположенная в одном месте. Пример: установка для испытаний магнитных материалов. 5. Измерительная система (ИС) – совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких физических величин, свойственных этому объекту, и выработки измерительных сигналов. Пример: измерительная система теплоэлектростанции, позволяющая получать измерительную информацию о ряде физических величин в разных энергоблоках. Она может содержать сотни измерительных каналов. 6. Измерительные принадлежности – вспомогательные средства, служащие для обеспечения необходимых условий для выполнения измерений с требуемой точностью. Примеры: источники электрического питания средств измерений; термостат и др. По метрологическому назначению средства измерений классифицируются: 1. Рабочее средство измерений – средство измерений, предназначенное для измерений, не связанных с передачей размера единицы другим средствам измерений. 2. Эталон единицы физической величины – средство измерений (или комплекс средств измерений), предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме средствам измерений и утвержденное в качестве эталона в установленном порядке.
ТЕМА 5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПОГРЕШНОСТЕЙ Определение погрешности
Качество средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия "погрешность" требует определения и четкого разграничения трех понятий: 1) истинное значение физической величины – значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину (истинное значение величины неизвестно, его применяют только в теоретических исследованиях. На практике используют действительное значение величины); 2) действительное значение физической величины – значение физической величены, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него; 3) результат измерения физической величины – значение величины, полученное путем ее измерения. Понятие "погрешность" – одно из центральных в метрологии, где используются два понятия: 1) погрешность результата измерения (Δхизм) – отклонение результата измерения (хизм) от истинного (действительного) значения измеряемой величины (хист(д)):
Δхизм = хизм – хист(д). (5.1) Она указывает границы неопределенности значения измеряемой величины; 2) погрешность средства измерений – разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых данным средством. Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам. К основным источникам возникновения погрешностей следует отнести примененного метода измерений; примененного средства измерения; условий проведения измерений; способу обработки результатов измерений; квалификации операторов и др.
Классификация погрешностей
Погрешности классифицируются по ряду признаков. Признак 1. По форме представления погрешности разделяются: 1) абсолютная погрешность Δ – погрешность измерения, выраженная в единицах измеряемой величины:
Δ = хизм – хист(д); (5.2)
2) относительная погрешность δ – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины:
3) приведенная погрешность – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона (нормирующее значение хн):
Нормирующее значение в зависимости от типа измерительного прибора, а также от вида его шкалы определяется следующими способами: 1) для средств измерений с равномерной, практически равномерной или степенной шкалой ХN следует устанавливать равным большему из пределов измерений:
или равным большему из модулей пределов измерений:
2) аналогично вышеуказанному случаю устанавливается ХN для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений; 3) для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений ХN допускается устанавливать равным сумме модулей пределов измерений:
4) для средств измерений физической величины, для которой принята шкала с условным нулем, ХN устанавливают равным модулю разности пределов измерений:
5) для средств измерений с установленным номинальным значением ХN устанавливают равным этому номинальному значению: ХN = хном (например, для мер); 6) для измерительных приборов с существенно неравномерной шкалой ХN устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах шкалы. Признак 2. По характеру изменения результатов при повторных измерениях погрешности разделяются: 1) систематическая погрешность – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Постоянные систематические погрешности свидетельствуют, прежде всего, о высоких или недостаточных показателях метрологической надежности применяемого средства измерения и могут быть устранены (учтены) предусмотренными аппаратурными методами коррекции или введением поправок в результаты измерений. Одной из распространенных систематических погрешностей является погрешность градуировки (погрешность нанесения делений на шкалу измерительного прибора). Данная погрешность легко выявляется, составляется таблица поправок, которая используется при определении результата измерений. Закономерно изменяющиеся систематические погрешности, возрастающие со временем эксплуатации средства измерения, как правило, квазимонотонно, называются прогрессирующими систематическими погрешностями. Они вызываются процессами старения узлов (комплектующих изделий) средства измерения (микросхем, резисторов, конденсаторов, и др.). Вследствие этого контролируемые и неконтролируемые параметры (характеристики) измерительных приборов изменяются и соответственно возрастают инструментальные погрешности средств измерений, по рассматриваемой классификационной группе относящиеся к систематическим. Старению подвержены и меры, например, концевые меры длины, гири. Это происходит из-за постепенного стирания поверхностей, окисления и других процессов. В некоторых случаях систематические погрешности могут изменяться периодически, в связи с чем они называются периодическими. Если систематическая погрешность постоянна для данного экземпляра средства измерения, то для большого числа средств измерений данного типа эта погрешность может более или менее отличаться случайным образом. Поэтому систематическая погрешность «ансамбля» приборов данного типа обычно рассматривается как случайная. Систематические погрешности наиболее просто выявить путем сопоставления результатов измерений физической величины, проведенных с помощью исследуемого средства измерения, и с помощью однородного – более точного; 2) случайная погрешность – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. В процессе любого измерения присутствуют многочисленные влияющие величины, учесть которые практически невозможно, но их совместное воздействие (случайная комбинация воздействий) сказывается на получении результатов измерений, а следовательно, и на погрешности измерений. В связи с этим до проведения измерений предсказать значение случайной погрешности невозможно. Случайная погрешность в отличие от систематической не может быть исключена из результата измерения, но ее влияние можно уменьшить с помощью многократных измерений искомой величины с последующим определением характеристик случайной погрешности методами математической статистики. Полученные при многократных измерениях результаты рассматриваются как случайные величины. К случайным погрешностям в большинстве случаев относятся и так называемые промахи (грубые погрешности) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубой погрешности чаще всего является неправильный отсчет показаний прибора. Иногда они могут возникать при скачкообразном изменении условий измерений (например, внезапное изменение напряжения питающей сети). При статистическом анализе промахи могут быть выявлены и соответствующие им результаты исключены. Признак 3. По причине возникновения погрешности разделяются: 1) инструментальная погрешность – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений. Данный вид погрешности определяется несовершенством средств измерений, неидеальной реализацией принципа действия, конструктивно-технологическими особенностями средства измерения и влиянием внешних условий. К инструментальным погрешностям обычно относят также помехи на входе средства измерения, вызываемые его подключением к объекту измерений. Инструментальная погрешность является одной из наиболее ощутимых составляющих погрешности, причем некоторые из инструментальных погрешностей являются систематическими, другие – случайными (например, за счет нестабильности параметров комплектующих изделий, входящих в измерительные цепи прибора); 2) погрешность метода измерений (методическая погрешность) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. Также к методическим относят погрешности, обусловленные несовершенством, недостатками примененного в средстве измерения метода измерений и упрощений при построении конструкции средства измерения, в том числе математических зависимостей; 3) субъективная погрешность – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора (степень внимательности, сосредоточенности, подготовленности). Эти погрешности практически отсутствуют при использовании автоматических или автоматизированных средств измерений; Признак 4. По условиям проведения измерений погрешности средств измерений разделяются: 1) основная погрешность – погрешность средства измерений, применяемого в нормальных условиях. Нормальные условия устанавливаются нормативно-техническими документами на виды средств измерений или отдельные их типы. Установление условий применения и особенно нормальных условий является весьма важным для обеспечения единообразия метрологических характеристик средств измерений. В противном случае погрешности средств измерений одного и того же типа, отнесенные к различным внешним условиям применения, будут несопоставимы. Выделение основной погрешности, соответствующей некоторым стандартным условиям применения, является одним из важных факторов обеспечения единства измерений. В большинстве нормативно-технических документов на средства измерений к нормальным относятся следующие внешние условия: - температура окружающей среды 293 К ± 5 К; - относительная влажность 65 % ± 15 %; - атмосферное давление 101,3 кПа ± 4 кПа (750 мм рт. ст. ± 30 мм рт. ст.); - напряжение питающей электрической сети (для электрических и других средств измерений, имеющих электрические цепи) 220 В ± 2 % с частотой 50 Гц. Для некоторых средств измерений допускается отклонение значений влияющих условий от нормальных. В этом случае кроме нормальных в техническом паспорте, техническом описании и других документах на тип средства измерений указываются рабочие условия, в пределах которых допускается эксплуатировать средства измерений с гарантированными метрологическими характеристиками (например, термопары могут эксплуатироваться при температурах от – 200 ºС до + 2800 ºС; 2) дополнительная погрешность – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений. Принято различать дополнительные погрешности по отдельным влияющим величинам (дополнительная температурная погрешность, дополнительная, погрешность за счет изменения атмосферного давления и т. д.). Как правило, наиболее значимой влияющей величиной является температура окружающей среды. Признак 5. По характеру изменения физической величины погрешности средства измерения разделяются: 1) статическая погрешность средства измерений – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную. 2) динамическая погрешность средства измерений – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины Проведенная классификация погрешностей измерений не является формальностью, с помощью которой можно детализировать их с тех или иных сторон представления, различия и причинности. Данная классификация широко используется при изучении погрешностей, в том числе с помощью воспроизведения (имитации) условий, при которых в процессе производства измерений проявляются соответствующие погрешности. Кроме этого, в большинстве случаев проведения экспериментов, когда результат измерений необходимо знать с погрешностью, не превышающей заданную, приходится учитывать общую погрешность измерений путем суммирования отдельных ее составляющих, различающихся по содержательным и количественным признакам.
5.3 Зависимость изменения погрешностей при различных формах их представления от значения измеряемой величины
По зависимости изменения значений погрешности от значения измеряемой величины абсолютная погрешность делится: 1) аддитивная (Δ = ± а):
Рисунок 5.1
В этом случае абсолютная погрешность не зависит от значения измеряемой величины и значение погрешности не изменяется; 2) мультипликативная (Δ = ± bх):
Рисунок 5.2
В этом случае абсолютная погрешность изменяется прямопропорционально изменению значения измеряемой величины; 3) смешанная, т.е. абсолютная погрешность имеет и аддитивную и мультипликативную составляющие (Δ = ± a + bx): В этом случае абсолютная погрешность имеет аддитивную составляющую на входе средства измерения, которая при изменении значения измеряемой величины также изменяется вследствие наличия мультипликативной составляющей. Рассмотренные выше случаи относятся к абсолютным погрешностям, имеющим линейную зависимость от изменения измеряемой величины. Если зависимость носит нелинейный характер, то такие погрешности называются нелинейными.
Рисунок 5.3
Изменение относительной погрешности в зависимости от изменения измеряемой величины связано с изменение абсолютной погрешности: 1) относительная погрешность определяется аддитивной абсолютной погрешностью (Δ = а; δ = Δ / х = а / х):
Рисунок 5.4
2) относительная погрешность определяется мультипликативной абсолютной погрешностью (Δ = bx; δ = Δ / х = b):
Рисунок 5.5
2) относительная погрешность определяется смешанной абсолютной погрешностью (Δ = а + bx; δ = Δ / х = b + а / х):
Рисунок 5.6
Характер изменения приведенной погрешности γ повторяет рассмотренные случаи изменения абсолютной погрешности, т.к. γ = Δ / хN, где хN – постоянная величина. В данном случае изменяется лишь масштаб зависимостей.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.009 с.) |

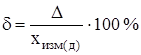 ; (5.3)
; (5.3) . (5.4)
. (5.4)












