
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Элементарная оценка погрешностей физических измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МеханикА Методические указания к лабораторным работам по физике для студентов 1-го курса технических специальностей всех форм обучения
Ростов-на-Дону Вводное занятие Тема: Элементарная оценка погрешностей физических измерений Физические измерения 1. Прямыми называются измерения, в которых значение измеряемой величины получается непосредственно в процессе измерения. Пример: измерение длины ¾ линейкой, времени ¾ секундомером, силы тока ¾ амперметром. 2. Косвенными называют измерения, в которых значение определяемой величины находят вычислением по формуле, в которую входят данные измерений других физических величин. Косвенными измерениями является, например, определение плотности тела по результатам измерений массы и размеров тела. 3. Классификация погрешностей (ошибок измерений). По происхождению погрешности можно разделить на три типа: систематические, случайные и промахи. Cистематические погрешности связаны с несовершенством средств и методов измерений. При многократном измерении одной и той же величины они сохраняются постоянными или меняются по определенному закону. Поэтому их можно полностью исключить введением поправок на показания приборов, их тщательной отладкой и т. д. Промахами называются погрешности, которые могут возникнуть в результате ошибочно отсчитанных или записанных показаний приборов, неисправностей или неверного подключения прибора и т. д. Измерения, содержащие промахи, следует отбрасывать. Случайные погрешности не подчиняются какому-либо закону и при многократном измерении одной и той же физической величины случайным образом меняют свое значение. Таким образом, систематические погрешности можно устранить, промахи следует отбросить, случайные погрешности оцениваются в теории погрешностей. 4. Вычисление погрешностей прямых измерений. Абсолютная погрешность измерения D х показывает на сколько полученный нами результат отличается от истинного. Для этого измерения проводят несколько раз. В качестве истинного значения измеряемой величины принимается среднее арифметическое значение результатов измерений:
где хi (i = 1, 2, 3, ¼n) ¾ результат i -го измерения; n ¾ число измерений. Далее необходимо найти абсолютную погрешность каждого из проведенных измерений: D хi = ê хi - х ср ê. В качестве абсолютной погрешности D х можно принять величину:
Результат принято записывать в виде: х = х ср ± D х. Относительная погрешность d х равна отношению абсолютной погрешности измерения к среднему значению измеряемой величины. d х = (D х / х ср). 5. Вычисление погрешностей косвенных измерений. При косвенных измерениях искомая величина является функцией других измеряемых величин, поэтому сначала, по заданной в методическом указании формуле, необходимо рассчитать относительную погрешность измерения d х, а затем определить абсолютную погрешность измерения D х = х эк d х. Ответ необходимо представить в виде: х = (х эк ± D х), d х = ¼. Лабораторная работа 1 - 1 Определение плотности твердых тел Лабораторная работа 1 - 2 Лабораторная работа 1 – 3 Изучение законов кинематики Поступательного и вращательного движения
Краткая теория Кинематика изучает механическое движение тел, не рассматривая причины, вызывающие это движение. Механические движение — изменение положения данного тела относительно другого тела или частей тела относительно других частей этого же тела, происходящее с течением времени. Тело отсчета — тело, относительно которого рассматривается данное механическое движение. Система отсчета — это система координат, связанная с телом отсчета и снабженная часами. Материальная точка — тело, размерами которого в данной задаче можно пренебречь. Траектория — линия, которую описывает материальная точка при своем движении. Перемещение Путь S (м) — расстояние, пройденное телом вдоль траектории движения. Путь — скалярная величина. Поступательное движение — движение, при котором все точки тела движутся по одинаковым траекториям. В этом случае тело можно считать материальной точкой. Скорость
Скорость направлена по касательной к траектории движения. Средняя путевая (скалярная) скорость равна отношению пути Δ S к времени движения D t:
Скалярная скорость v (скорость движения) — скалярная величина, равная первой производной от пути по времени:
Прямолинейное равномерное движение — движение, при котором тело движется вдоль прямой линии с постоянной по величине скоростью. Путь при равномерном движении прямо пропорционален времени движения: S = vt. Ускорение
Тангенциальное ускорение характеризует быстроту изменения величины скорости и равно первой производной от величины скорости по времени:
Тангенциальное ускорение направлено по касательной к траектории движения. Нормальное (центростремительное) ускорение характеризует быстроту изменения скорости по направлению и направлено к центру кривизны траектории:
где R — радиус кривизны траектории. Полное у скорение тела есть геометрическая сумма тангенциального и нормального ускорений:
Прямолинейное равнопеременное движение — движение тела по прямой линии с постоянным тангенциальным ускорением. Путь S и скорость v при равнопеременном движении изменяются по законам:
Знак ²+² соответствует равноускоренному, а знак²─² — равнозамедленному движению; Вращательное движение — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Угловая скорость
Вектор Угловое ускорение
Вектор Связь между линейными и угловыми величинами:
Порядок выполнения работы Задание 1. Исследование равномерного движения 1. Установить систему в исходное состояние: правый груз должен находиться напротив отметки «0» шкалы. Убедиться, что система находится в равновесии. 2. Положить на правый груз перегрузок, заданный преподавателем. 3. Кольцевую платформу установить напротив отметки шкалы h заданной преподавателем. 4. Отпустить грузы так, чтобы они начали свободно двигаться. 5. В момент прохождения правого груза сквозь кольцевую платформу, включить секундомер. Так как перегрузок задерживается кольцевой платформой, то дальнейшее движение основного груза будет равномерным. 6. Выключить секундомер, когда груз пройдет заданное расстояние S. Повторить опыт 3 раза. Результаты измерений занести в таблицу №1. 7. Повторить пункты 1-7 для других значений S.
Таблица №1
8. Построить график зависимости пути S от среднего времени движения S = f(t ср.). В качестве экспериментальной кривой следует выбрать прямую линию, проходящую через начало координат. Число точек сверху и снизу от этой прямой должно быть примерно одинаковым. 9. С помощью графика рассчитать скорость равномерного движения грузов по формуле: v = S/t ср. 10. По графику оценить погрешность измерения скорости. Задание 2. Исследование равноускоренного движения 1. Снять кольцевую платформу. 2. Установить систему в исходное состояние: правый груз должен находиться напротив отметки «0» шкалы. Убедиться, что система находится в равновесии. 3. Положить на правый груз перегрузок, заданный преподавателем. 4. Одновременно включить секундомер и отпустить грузы так, чтобы они начали свободно двигаться. 5. Выключить секундомер, когда груз пройдет заданное расстояние S. Повторить опыт 3 раза. Результаты измерений занести в таблицу №2. 6. Повторить пункты 1-5 для других значений S. 7. Рассчитать ускорение для каждого значения S по формуле: a = 2 S / t ср2. 8. Найти среднее значение ускорения грузов. 9. Оценить погрешность измерения ускорения для указанного преподавателем номера измерения по формулам:
δ а = Δ S/S + 2Δ t/t ср, Δ а = а∙ δ а. 10. Рассчитать Таблица №2
Контрольные вопросы 1. Что изучает кинематика? 2. Что такое механическое движение, тело отсчета и система отсчета? 3. Дайте определения материальной точки, траектории движения, пути и перемещения. 4. Приведите формулы скорости и средней скорости движения. 5. Какое движение называется равномерным прямолинейным? 6. Приведите формулу пути при равномерном движении. 7. Что такое ускорение, тангенциальное и нормальное ускорение? 8. Какое движение называется равнопеременным? 9. Приведите формулы пути и скорости при равнопеременном движении. 10. Приведите формулы угловой скорости и углового ускорения. 11. Как определить направления угловой скорости и углового ускорения? 12. Напишите формулы связи между линейными и угловыми величинами. Лабораторная работа № 1-4 Лабораторная работа № 1-5 Изучение законов динамики Поступательного движения
Теоретические сведения Динамика изучает причины, вызывающие механическое движение. Инерция — способность тела сохранять состояние покоя или прямолинейного равномерного движения, если на это тело не действуют другие тела. Масса m (кг) — количественная мера инертности тела. Первый закон Ньютона: Существуют такие системы отсчета, в которых тело находится в состоянии покоя или прямолинейного равномерного движения, если на него не действуют другие тела. Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Сила Принцип суперпозиции сил: Если на материальную точку действуют одновременно силы
Импульс тела
Второй закон Ньютона:
где Замечание. Если масса тела постоянна, то второй закон Ньютона принимает вид:
где Сила тяжести Вблизи поверхности Земли тело массой m под действием силы тяжести
Порядок выполнения работы Задание 1. Определение зависимости ускорения системы грузов от действующей внешней силы. 1. Установить на правый груз перегрузок заданной массы Δ m и определить время, за которое груз проходит заданное преподавателем расстояние S. Время прохождения расстояния измерить три раза. Данные измерений записать в таблицу 1. 2. Повторить измерения п.1 для других перегрузков. 3. Рассчитать ускорения системы грузов по формуле
4. Рассчитать теоретическую зависимость ускорения от силы тяжести перегрузка по формуле a теор = Δ mg / M. 5. Построить в одной системе координат графики зависимости экспериментальных и теоретических значений ускорения системы грузов от величины силы тяжести перегрузка Δmg.
Таблица 1 Задание 2. Определение зависимости ускорения системы грузов от их массы.
1. Уменьшить массу системы грузов вдвое (для этого необходимо отвинтить нижнюю половину каждого из грузов). 2. Повторно провести измерения с новой системой грузов для одного перегрузка (см.задание 1). Занести результаты измерений в таблицу 2.
Таблица 2
3. Рассчитать ускорение системы грузов по формуле
4. Рассчитать теоретическое значение ускорения от силы тяжести перегрузка по формуле a теор = 2Δ mg / M. 5. Сделать вывод на основе сравнения значений ускорений в задании 1 и 2. Контрольные вопросы 1. Что изучает динамика? 2. Что такое инерция? 3. Дайте определения массы, силы и ускорения. 4. Сформулируйте принцип суперпозиции сил. 5. Сформулируйте первый закон Ньютона. 6. Какие системы отсчета называют инерциальными? 7. Что такое импульс тела? 8. Сформулируйте второй закон Ньютона. 9. Что такое сила тяжести? 10.Выведите формулу зависимости ускорения системы грузов от их массы на машине Атвуда. Лабораторная работа № 1 - 6 Лабораторная работа № 1 - 7 Лабораторная работа 1 - 8 Лабораторная работа 1 - 9 Лабораторная работа 1 - 10 МеханикА Методические указания к лабораторным работам по физике для студентов 1-го курса технических специальностей всех форм обучения
Ростов-на-Дону Вводное занятие Тема: Элементарная оценка погрешностей физических измерений Физические измерения 1. Прямыми называются измерения, в которых значение измеряемой величины получается непосредственно в процессе измерения. Пример: измерение длины ¾ линейкой, времени ¾ секундомером, силы тока ¾ амперметром. 2. Косвенными называют измерения, в которых значение определяемой величины находят вычислением по формуле, в которую входят данные измерений других физических величин. Косвенными измерениями является, например, определение плотности тела по результатам измерений массы и размеров тела. 3. Классификация погрешностей (ошибок измерений). По происхождению погрешности можно разделить на три типа: систематические, случайные и промахи. Cистематические погрешности связаны с несовершенством средств и методов измерений. При многократном измерении одной и той же величины они сохраняются постоянными или меняются по определенному закону. Поэтому их можно полностью исключить введением поправок на показания приборов, их тщательной отладкой и т. д. Промахами называются погрешности, которые могут возникнуть в результате ошибочно отсчитанных или записанных показаний приборов, неисправностей или неверного подключения прибора и т. д. Измерения, содержащие промахи, следует отбрасывать. Случайные погрешности не подчиняются какому-либо закону и при многократном измерении одной и той же физической величины случайным образом меняют свое значение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.110 (0.009 с.) |

 ,
, .
. (м) — вектор, соединяющий начальное и конечное положения материальной точки. Модуль перемещения ï
(м) — вектор, соединяющий начальное и конечное положения материальной точки. Модуль перемещения ï  ï — скалярная величина, равная длине этого вектора.
ï — скалярная величина, равная длине этого вектора. (м/с) — физическая векторная величина, характеризующая быстроту изменения положения тела в пространстве с течением времени и равная первой производной от вектора перемещения по времени:
(м/с) — физическая векторная величина, характеризующая быстроту изменения положения тела в пространстве с течением времени и равная первой производной от вектора перемещения по времени:
 .
.  .
.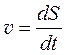 .
. (м/с2) — физическая векторная величина, характеризующая быстроту изменения скорости с течением времени и равная первой производной от скорости по времени:
(м/с2) — физическая векторная величина, характеризующая быстроту изменения скорости с течением времени и равная первой производной от скорости по времени: .
.
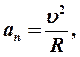

 ,
, 
 .
. — скорость тела в момент времени t = 0.
— скорость тела в момент времени t = 0. (рад/с) — физическая векторная величина, равная первой производной угла поворота тела по времени:
(рад/с) — физическая векторная величина, равная первой производной угла поворота тела по времени:
 (рад/с2) — физическая векторная величина, равная первой производной угловой скорости тела по времени:
(рад/с2) — физическая векторная величина, равная первой производной угловой скорости тела по времени:

 для любой крайней точки блока для указанного преподавателем номера измерения и показать их направления.
для любой крайней точки блока для указанного преподавателем номера измерения и показать их направления.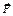 (Н) — векторная величина, характеризующая взаимодействие между телами или частями тела.
(Н) — векторная величина, характеризующая взаимодействие между телами или частями тела. и
и 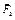 , то их можно заменить равнодействующей силой
, то их можно заменить равнодействующей силой 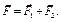
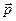 (кг∙м/с) — векторная величина, равная произведению массы m материальной точки на его скорость
(кг∙м/с) — векторная величина, равная произведению массы m материальной точки на его скорость 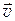 :
: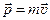 ,
,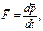
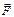 — равнодействующая сила, действующая на материальную точку.
— равнодействующая сила, действующая на материальную точку.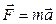 ,
,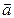 — ускорение, приобретаемое телом массой m под действием силы
— ускорение, приобретаемое телом массой m под действием силы 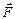 .
.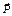 — сила, действующая на тело вследствие его притяжения к Земле или другим небесным телам.
— сила, действующая на тело вследствие его притяжения к Земле или другим небесным телам.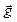 . Поэтому по второму закону Ньютона сила тяжести равна:
. Поэтому по второму закону Ньютона сила тяжести равна: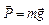 .
. .
. кг
кг

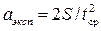 .
.


