
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Общие сведения о метрологии и измерении физических величин.Содержание книги
Поиск на нашем сайте МЕТРОЛОГИЯ Программа,, методические указания, вопросы для самопроверки и контрольные задания для студентов II, III курсов заочной формы обучения НОВОСИБИРСК
Составители: В.К. Береснев, канд. техн. наук, доц., Г.Г. Матушкин, канд. техн. наук, доц.,
Рецензент
Работа подготовлена на кафедре Систем сбора и обработки данных
Предисловие
Предлагаемое методическое пособие включает в себя краткое, изложение основных разделов дисциплины, вопросы для самопроверки, контрольные задания и список литературы. В результате изучения дисциплины «Метрология» студенты должны: - ознакомится с принципами действия, основными характеристиками и областями применения средств электрических измерений; - освоить основные методы нормирования погрешностей средств измерений и уметь оценить погрешность результата измерений; - уметь самостоятельно выбрать метод и средство измерения в зависимости от требуемой точности и условий проведения эксперимента. Рекомендуемая литература 1.Основы метрологии и электрические измерения. Учебник для вузов /Б.Я. Авдеев, Е.М. Антонюк, Е.М. Душин и др.; Под ред. Е.М. Душина – 6-е изд., переработ. и доп.- Л.: Энергоатомиздат. Ленингр.отд-ние, 1987.- 480 с. 2. Тартаковский Д.Ф., Ястребов А.С. Метрология, стандартизация и технические средства измерений: Учебн. для вузов. – М.: Высш. шк., 2001. – 205 с. 3. Метрология и электрорадиоизмерения в телекоммутационных системах: Учебник для вузов /В.И. Нефёдов, В.И. Хахин, Е.В. Федорова и др.; Под ред. В.И. Нефёдова. – М.: Высш. шк.,2001. – 383 с. 4. Э.Г. Атамалян. Приборы и методы измерения электрических величин: Учеб. пособие для студ. втузов. – 2 изд., перераб. и доп. - М.: Высш.шк., 1989. – 384 с. 5. Тревис Дж. LabVIEW для всех/Пер с англ.Клушин Н.А. – М.:ДМК Пресс; ПриборКомплект,2005 – 544 с. 6. Батоврин В.К., Бессонов А.С., Мошкин В.В. LabVIEW: практикум по электронике и микропроцессорной технике: Учебное пособие для вузов. – М. ДМКПресс, 2005. -182 с.
Содержание стр. Введение………………………………………………………………….4 I. Общие сведения о метрологии и измерении физических величин……………………………………………………………4 II. Погрешности измерений…………………………………………8 III. Измерительные преобразователи и интеллектуальные датчики……………………………………………………………26 IV. Электромеханические и электронные аналоговые измерительные приборы………………………………………….28 V. Измерительные мосты и компенсаторы постоянного и переменного тока………………………………………………….31 VI. Цифровые измерительные приборы……………………………..32 VII. Приборы для анализа сигналов…………………………………..45 VIII. Виртуальные измерительные приборы………………………….47 IX. Системы сбора и обработки измерительной информации……..49 X. Основы стандартизации и сертификации……………………….49 XI. Контрольные работы……………………………………………...51 Введение
Роль метрологии и технических средств измерений в развитии научно-технического прогресса. Краткий исторический обзор развития Метрологии и технических средств измерений [ 1: с.4 … 9; 2: с.6…11; 3: с.7…12; 4: с.6…11].
II. Погрешности измерений Источники погрешностей (инструментальные и методические погрешности, влияние помех, субъективные ошибки). Номинальная и реальная функция преобразования, абсолютная и относительная погрешность средства измерений, основная и дополнительная погрешности. Пределы допускаемых погрешностей, классы точности средств измерений. Выявление и уменьшение систематических погрешностей. Оценка случайных погрешностей. Доверительный интервал и доверительная вероятность. Оценка погрешностей косвенных измерений. Обработка результатов измерений. [ 1: с.23…35,40,41,53,54,56…61; 2: с.22…53; 3: с.48…91; 4: с.21,22,35…52,63…71, 72…77,85…93].
II.1. Основные сведения и методические указания. Одним из основополагающих понятий Метрологии является понятие погрешности измерений.
Погрешностью измерения называют отклонение измеренного В случае применения средства измерений в нормальных условиях Эксплуатации. Номенклатура влияющих на средство измерений величин и диапазоны их изменений определяются разработчиками в качестве нормальных условий для каждого типа средств измерений. Нормальные условия эксплуатации всегда указываются в техническом паспорте средства измерений. Если эксперимент выполняется в условиях, отличных от нормальных для данного средства измерений, его реальная характеристика искажается сильнее, чем в нормальных условиях. Погрешности, которые при этом возникают, называют дополнительными.
Дополнительной погрешностью называют погрешность средств Эксплуатации. Рабочие условия эксплуатации, так же как и нормальные, в обязательном порядке приводятся в техническом паспорте средств измерений. Инструментальная погрешность средств измерений определенного типа не должна превышать некоторого заданного значения – так называемой предельно допустимой основной погрешности средств измерений данного типа. Фактическая основная погрешность каждого конкретного экземпляра этого типа является при этом случайной величиной и может принимать различные значения, иногда даже равные нулю, но в любом случае инструментальная погрешность не должна превышать заданного предельного значения. Если это условие не выполняется, средство измерений должно быть изъято из обращения.
Методическими называются погрешности, которые возникают из-за неудачного выбора экспериментатором средства измерения для решения поставленной задачи. Они не могут быть приписаны средству измерения и приведены в его паспорте. Методические погрешности измерения зависят как от характеристик применяемого средства измерений, так и во многом от параметров самого объекта измерения. Неудачно выбранные средства измерений могут исказить состояние объекта измерений. При этом методическая составляющая погрешности может оказаться существенно больше инструментальной.
Субъективными погрешностями называют погрешности, Измерений.
Этот тип погрешностей связан обычно с невнимательностью экспериментатора: применение прибора без устранения смещения нуля, неправильное определение цены деления шкалы, неточный отсчет доли деления, ошибки в подключении и т.п.
3. По характеру проявления погрешности измерений подразделяют на: - систематические погрешности; - случайные погрешности; - промахи (грубые ошибки).
Систематической называют погрешность, которая при повторных измерениях одной и той же величины остается постоянной, или изменяется закономерно. Систематические погрешности обусловлены как несовершенством метода измерений и влиянием средства измерений на измеряемый объект, так и отклонением реальной передаточной характеристики применяемого средства измерений от номинальной характеристики. Постоянные систематические погрешности средств измерений могут быть выявлены и численно определены в результате сличения их показаний с показаниями эталонных средств измерений. Такие систематические погрешности могут быть уменьшены регулировкой приборов или введением соответствующих поправок. Следует заметить, что полностью исключить систематические погрешности средств измерений не удается, так как их реальные передаточные характеристики изменяются при изменении условий эксплуатации. Кроме этого всегда имеют место так называемые прогрессирующие погрешности (возрастающие или убывающие), вызванные старением элементов входящих в состав средств измерений. Прогрессирующие погрешности могут быть скорректированы регулировкой или введением поправок лишь на некоторое время. Таким образом, даже после регулировки или введения поправок, всегда имеет место так называемая неисключенная систематическая погрешность результата измерений.
Случайной называют погрешность, которая при повторных измерениях одной и той же величины принимает различные значения. Случайные погрешности обусловлены хаотичным характером изменений физических величин (помех), влияющих на передаточную характеристику средства измерений, суммированием помех с измеряемой величиной, а также наличием собственных шумов средства измерений. При создании средств измерений предусматриваются специальные меры защиты от помех: экранирование входных цепей, использование фильтров, применение стабилизированных источников питающего напряжения и т.д. Это позволяет уменьшить величину случайных погрешностей при проведении измерений. Как правило, при повторных измерениях одной и той же величины результаты измерений либо совпадают, либо отличаются на одну, две единицы младшего разряда. В такой ситуации случайной погрешностью пренебрегают и оценивают только величину неисключенной систематической погрешности. Наиболее сильно случайные погрешности проявляются при измерении малых значений физических величин. Для повышения точности в таких случаях производятся многократные измерения с последующей статистической обработкой результатов методами теории вероятности и математической статистики.
Промахами называют грубые погрешности, существенно превышающие ожидаемые погрешности при данных условиях проведения измерений. Промахи большей частью возникают из-за субъективных ошибок экспериментатора или из-за сбоев в работе средства измерений при резких изменениях условий эксплуатации (броски или провалы сетевого напряжения, грозовые разряды и т.п.) Обычно промахи легко выявляются при повторных измерениях и исключаются из рассмотрения. Оценка погрешностей косвенных измерений. При косвенных измерениях результат измерений определяется по функциональной зависимости от результатов прямых измерений. Поэтому погрешность косвенных измерений определяется как полный дифференциал этой функции от величин, измеряемых с помощью прямых измерений.
Где: измерений;
измерения;
величинами, подвергающимися прямым измерениям.
Статистическая обработка результатов измерений
Из-за влияния на средство измерений помех различного происхождения (изменение температуры окружающей среды, электромагнитных полей, вибраций, изменения частоты и амплитуды сетевого напряжения, изменения атмосферного давления, влажности и т.д.), а также из-за наличия собственных шумов элементов, входящих в состав измерительных приборов, результаты повторных измерений одной и той же физической величины (особенно ее малых значений) будут в большей или меньшей степени отличаться друг от друга. В этом случае результат измерений является случайной величиной, которая характеризуется наиболее вероятным значением и разбросом (рассеянием) результатов повторных измерений вблизи наиболее вероятного значения. Если при повторных измерениях одной и той же величины результаты измерений не отличаются друг от друга, то это означает, что разрешающая способность отсчетного устройства не позволяет обнаружить это явление. В этом случае случайная составляющая погрешности измерений является несущественной и ею можно пренебречь. При этом неисключенную систематическую погрешность результата измерений оценивают по величине пределов допускаемых погрешностей применяемых средств измерений. Если же при повторных измерениях одной и той же величины наблюдается разброс показаний, то это означает, что наряду с большей или меньшей неисключенной систематической погрешностью, имеет место и случайная погрешность, принимающая при повторных измерениях различные значения. Для определения наиболее вероятного значения измеряемой величины при наличии случайных погрешностей и для оценки погрешности, с которой определено это наиболее вероятное значение, применяется статистическая обработка результатов измерений. Статистическая обработка результатов серии измерений при проведении экспериментов позволяет решить следующие задачи. 1. Более точно определить результат измерения путем усреднения отдельных наблюдений. 2. Оценить область неопределенности уточненного результата измерений. Основной смысл усреднения результатов измерений заключается в том, что найденная усредненная оценка имеет меньшую случайную погрешность, чем отдельные результаты, по которым эта усредненная оценка определяется. Следовательно усреднение не устраняет полностью случайного характера усредненного результата, а лишь уменьшает ширину полосы его неопределенности. Таким образом, при статистической обработке, прежде всего, определяют наиболее вероятное значение измеряемой величины путем вычисления среднего арифметического всех отсчетов:
где: xi – результат i – го измерения; n – число проведенных измерений в данной серии измерений. После этого оценивают отклонение результатов отдельных измерений xi от этой оценки среднего значения Затем находят оценку среднеквадратического отклонения
Точность оценки наиболее вероятного значения измеряемой величины
Следовательно, точность результата многократных измерений увеличивается с ростом числа последних. Однако в большинстве практических случаев нам важно определить не просто степень рассеивания значения погрешности при проведении серии измерений (т.е. величину
Доверительным интервалом
При определении доверительных интервалов необходимо, прежде всего, учитывать, что закон распределения погрешностей, получаемых при проведении многократных измерений, при числе измерений в серии меньше 30, описывается не нормальным законом распределения, а так называемым законом распределения Стьюдента. И, в этих случаях, величину доверительного интервала обычно оценивают по формуле:
где В табл.4.1 приведены значения коэффициентов Стьюдента Таблица 4.1 Значения коэффициентов Стьюдента
При изучении материалов данного раздела следует хорошо уяснить, что погрешности результатов измерений и погрешности средств измерений – не идентичные понятия. Погрешность средства измерения это его свойство, характеристика, для описания которого используют ряд правил, закрепленных в стандартах и нормативных документах. Это та доля погрешности измерения, которая определяется только самим средством измерения. Погрешность же измерений (результата измерений) – это число, которое характеризует границы неопределенности значения измеряемой величины. В нее, кроме погрешности средства измерений, могут входить составляющие погрешности, порожденные применяемым методом измерения (методические погрешности), действием влияющих (неизмеряемых) величин, погрешность отсчета и др. Нормирование погрешностей средств измерения.
Точность СИ определяется предельно-допустимыми погрешностями, которые могут быть получены при его использовании.
И переменного тока. Мосты для измерения сопротивления на постоянном токе. Мосты переменного тока для измерения емкости и угла потерь конденсаторов, индуктивности и добротности катушек. Потенциометры постоянного тока для измерения ЭДС, напряжений, тока. Структурные схемы и принцип функционирования. [ 1: с.186…212; 2: с.79, 80, 102…107; 3: с.133, 134, 269…272; 4: с.219…225, 284…296].
V.1. Основные сведения и методические указания. Измерительные мосты и компенсаторы относятся к измерительным приборам, использующим метод непосредственного сравнения измеряемой величины с мерами, включенными в структуру прибора. Общая их особенность состоит в том, что для получения результата необходимо выполнить ряд операций, приводящих измерительную цепь в состояние равновесия. Мостовые измерительные схемы широко используются для измерения параметров элементов электрических цепей. При изучении мостовых цепей необходимо ознакомится с основными соотношениями, конфигурациями схем, рассмотреть чувствительность как важную метрологическую характеристику любого прибора сравнения. Потенциометры постоянного тока используются для точных измерений напряжений. Обратите внимание на своеобразный принцип действия, основные элементы потенциометра, на оценку погрешности данного средства измерений. Компенсаторы переменного тока имеют более сложные уравнения равновесия, так как в этом случае для уравновешивания двух напряжений необходимо обозначить равенство напряжений по модулю, противоположность по фазе, равенство частоты и идентичность формы кривой.
V.2. Вопросы для самопроверки. 1. Чем ограничивается нижний и верхний пределы измерений активных сопротивлений одинарными мостами постоянного тока? 2. Изобразите схему простейшего моста для измерения емкости; для измерения индуктивности. 3. Можно ли уравновесить мост переменного тока при произвольном характере сопротивлений плеч? 4. Почему с помощью потенциометров возможно измерение ЭДС источника? 5. Объясните функциональные схемы автоматического моста и автоматического компенсатора? 6. Что применяется в качестве индикатора равновесия в мостах постоянного тока? 7. Какими приборами измеряют добротность катушек индуктивности? 8. Какие преимущества имеет четырехзажимное включение измеряемого резистора в схему одинарного моста. 9. Как изменится чувствительность моста постоянного тока, если включить дополнительный резистор в диагональ питания? 10. Чем обусловлена погрешность мостов постоянного тока? 11. Чем обусловлена погрешность мостов переменного тока? 12. Какие индикаторы равновесия применяются в мостах переменного тока?
Таким образом, технология виртуальных приборов опирается на современную компьютерную технику в комбинации с гибким специальным программным обеспечением и модульным высокопроизводительным оборудованием для создания мощных компьютерных измерительных систем. Современные виртуальные измерительные приборы позволяют измерять и анализировать как локальные, так и удаленные величины и процессы со временем измерения десятки наносекунд и погрешностью в сотые и тысячные доли процента. Их возможности в настоящее время возросли настолько, что даже превосходят аналогичные показатели традиционных приборов. Они позволяют с легкостью осуществлять такую обработку измерительных сигналов как частотно-временной анализ, спектральный анализ высокого разрешения, цифровую фильтрацию, различного рода статистическую обработку и пр. При этом они позволяют наглядно отображать на экране дисплея значения измеряемых величин, осциллограммы различных процессов, их амплитудно-частотные характеристики как двумерные, так и в виде объемных графических изображений, спектральные плотности и гистограммы статистической обработки и т.п. Наиболее известной фирмой, разрабатывающей как аппаратные модули, так и программное обеспечение, является фирма National Instruments (NI). Разработанные ею аппаратные модули и специализированное программное обеспечение виртуальных приборов под общим названием LabVIEW (Laboratory Virtual Instrument Engineering Workbench – лабораторный виртуальный прибор рабочего места инженера), получило широкое распространение, улучшается и расширяется с каждым годом и охватывает огромный спектр возможностей как управления процессом измерения, так и методов обработки и отображения результатов измерения.
VIII.2 Вопросы для самопроверки 1. Что понимается под виртуальным измерительным прибором? 2. Из каких основных частей состоит виртуальный измерительный прибор? 3. Какие новые возможности измерений открываются при использовании виртуальных измерительных приборов? XI. Контрольные работы. Контрольная работа №1 (Погрешности измерений)
Задача №1 При измерении активного сопротивления резистора было произведено десять равноточных измерений, результаты которых приведены в табл.1.1. Оцените максимальную и относительную погрешности измерений и запишите результат эксперимента в виде доверительного интервала для двух значений доверительной вероятности
Табл.1.1
Задача №2 Определить величину электрического тока I
Таблица 1.2
Рис.1.2
Задача №3 Производится эксперимент по определению параметров транзисторов
Таблица 1.3
Задача №4 Определить значение и предельную абсолютную погрешность сопротивления резистора, намотанного из медного провода диаметром D и длиной L, если предельная абсолютная погрешность диаметра провода и его длины соответственно равны:
Таблица 1.4
Контрольная работа № 2 (Поверка и функционирование средств измерений)
Задача №1 При поверке после ремонта вольтметра класса точности 1,5 с конечным значением шкалы 5В, в точках шкалы 1,2,3,4,5 В, получены показания образцового прибора, представленные в табл.2.1. Определить, соответствует ли поверяемый вольтметр своему классу точности?
Таблица 2.1
Задача №2 Изобразите осциллограмму, которая будет на экране осциллографа, если на пластины Y подать синусоидальное напряжение с частотой F и амплитудой Um (см. табл. 2.2). Время нарастания пилообразного напряжения развертки, поступающего на пластины X равно t1, время его спада – t2. Во время обратного хода луча электронно-лучевая трубка осциллографа не запирается. Определите также величину максимального отклонения луча по оси Y для заданного Um, если при подаче на вход осциллографа сигнала синусоидальной формы со среднеквадратическим значением 5 В было получено отклонение h.
Таблица 2.2.
Задача № 3 Изобразите
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.014 с.) |

 ;
; 

 - предельные абсолютные погрешности результатов прямых
- предельные абсолютные погрешности результатов прямых - предельная абсолютная погрешность результата косвенного
- предельная абсолютная погрешность результата косвенного - соответствующие предельные относительные погрешности.
- соответствующие предельные относительные погрешности. - функциональная связь между искомой измеряемой величиной и
- функциональная связь между искомой измеряемой величиной и
 -
-  .
. наблюдений, характеризующую степень рассеяния результатов отдельных наблюдений вблизи
наблюдений, характеризующую степень рассеяния результатов отдельных наблюдений вблизи  , по формуле:
, по формуле: .
. . Нетрудно убедиться в том, что результаты нескольких оценок
. Нетрудно убедиться в том, что результаты нескольких оценок  . Эта оценка характеризует степень разброса значений
. Эта оценка характеризует степень разброса значений  может быть оценена систематическая составляющая результата серии измерений. Для различных
может быть оценена систематическая составляющая результата серии измерений. Для различных 

 называют интервал, который с заданной вероятностью, называемой доверительной вероятностью
называют интервал, который с заданной вероятностью, называемой доверительной вероятностью  накрывает истинное значение измеряемой величины.
накрывает истинное значение измеряемой величины. ,
, - так называемый коэффициент Стьюдента.
- так называемый коэффициент Стьюдента. .
.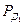 = 0,95 и
= 0,95 и  = 0,99.
= 0,99. в общей цепи (рис.1.2), а также значения абсолютной и относительной погрешности его определения, если токи, измеренные в ветвях цепи, равны I
в общей цепи (рис.1.2), а также значения абсолютной и относительной погрешности его определения, если токи, измеренные в ветвях цепи, равны I  ,I
,I  ,I
,I  , классы точности амперметров, включенных в эти ветви, соответствуют К
, классы точности амперметров, включенных в эти ветви, соответствуют К 






 и
и  . Для этого измеряются микроамперметрами ток коллектора -
. Для этого измеряются микроамперметрами ток коллектора -  и ток эмиттера -
и ток эмиттера -  , а затем определяются параметры
, а затем определяются параметры  ,
,  . Представьте результаты определения указанных параметров вместе с погрешностями их определения. Предел измерения используемых микроамперметра, их классы точности и полученные показания приведены в таблице 1.3.
. Представьте результаты определения указанных параметров вместе с погрешностями их определения. Предел измерения используемых микроамперметра, их классы точности и полученные показания приведены в таблице 1.3. мкА
мкА
 мкА
мкА
 и
и  Определение значения сопротивления осуществляется по формуле:
Определение значения сопротивления осуществляется по формуле:  , где
, где  = 3,14+0,0016, а
= 3,14+0,0016, а  .
.





