Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммирование погрешностей измерений. Оценка результатов косвенных измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Суммированием погрешностей называют определение расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих. Если составляющие погрешности подчиняются разным законам распределения и их количество велико, то их суммирование с выявлением функции многомерного распределения представляет неразрешимую задачу. На практике суммирование заключается, как правило, в определении среднего квадратического отклонения Простейшим случаем, при котором возникает необходимость суммирования погрешностей, является нахождение искомой величины как суммы нескольких составляющих
Если суммируемых составляющих более пяти, то можно утверждать, что распределение случайной погрешности суммы будет близко к нормальному. Для построения доверительного интервала в этом случае можно применить функцию Лапласа. Если при определении составляющих погрешностей используют измерительные средства с известными предельными погрешностями, заданными из условия трех сигм
Погрешность суммы в этом случае не выйдет за пределы полученного значения с вероятностью 0,997. Приведенные формулы используются при расчете допуска замыкающего звена размерных цепей в системе обеспечения геометрической точности в строительстве. Другая наиболее часто встречающаяся функциональная зависимость, используемая при косвенных измерениях, выражается уравнением:
Где В этом случае относительное среднеквадратическое отклонение (коэффициент вариации) результирующей величины определяется по формуле:
При суммировании составляющие погрешности могут значительно отличаться по величине. Наименьшие из них иногда не влияют на точность определения суммарной погрешности и, следовательно, ими можно пренебрегать с целью упрощения вычислений. Для этой цели устанавливают критерий ничтожно малой погрешности, т.е. правило, позволяющее исключать ее из расчета. Наиболее часто используют следующее правило: наименьшую случайную погрешность можно не учитывать, если ее среднеквадратическое отклонение Выбор средств измерений Учет всего комплекса метрологических характеристик необходим только при измерениях высокой точности, а также при проектировании сложных измерительных систем. В большинстве производственных отраслей, в том числе в строительстве, используют рабочие средства измерений, метрологические характеристики которых нормированы на основе классов точности. Класс точности — обобщенная характеристика средств измерений определенного типа, позволяющая судить о том, в каком диапазоне находится суммарная погрешность измерений. Совокупность метрологических характеристик, определяющих класс точности, отражается в стандартах или технических условиях. Средствам измерений с несколькими диапазонами измерений одной и той же физической величины или предназначенным для измерений разных физических величин могут быть присвоены различные классы точности для каждого диапазона или каждой измеряемой величины. Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений. При этом в эксплуатационной документации на средства измерений, содержащей обозначение класса точности, должна быть ссылка на стандарт или технические условия, в которых установлен класс точности для этого типа средств измерений. Обозначения могут иметь форму заглавных букв латинского алфавита или римских цифр с добавлением условных знаков. Смысл таких обозначений раскрывается в нормативно-технической документации. Если же класс точности обозначается арабскими цифрами с добавлением какого-либо знака, то эти цифры непосредственно оценивают погрешность измерения. Для выражения допускаемых основных погрешностей при их нормировании и оценке используют различные способы, в зависимости от того, какой из них наиболее соответствует характеру средства измерений. Например, для гирь, штангенинструмента, концевых мер длины указывают значения абсолютных допускаемых погрешностей Если нормируется допустимая относительная погрешность
где Класс точности при этом обозначается числом из того же ряда, что и при нормировании относительной погрешности, но дополнительного значка при этом нет. Например, если вольтметр класса 1,5 с диапазоном измерений от 0 до 250 В показывает напряжение 36 В, то абсолютная погрешность измерения, В, составит: Шкалы некоторых приборов градуируют в миллиметрах, абсолютная погрешность при этом выражается также в единицах длины. Если для такого прибора нормируется значение приведенной погрешности, то класс точности прибора обозначается в виде 1,0, где 1,0 — значение приведенной погрешности, выраженное в процентах. Выбор средств измерений для конкретных измерительных целей определяется многими факторами. Задача выбора может быть как очень простой, так и достаточно сложной, когда требуется проверка соответствия свойств средства измерения предъявляемым требованиям по быстродействию, надежности, степени защищенности от определенных воздействий и т. п. Но главным требованием является, как правило, обеспечение необходимой точности измерений. Для обоснования этого требования необходимо знать цель измерения. Таких целей две. Они имеют следующие принципиальные отличия: • определение действительного размера измеряемой величины в заданных единицах; • определение соответствия измеряемой величины предписанному (номинальному) размеру, для которого заданы допустимые предельные отклонения. В первом случае измеряемой величине присваивается размер, достоверность которого полностью определяется погрешностью, имевшей место в момент измерения. Допустимая погрешность назначается исходя из конкретных задач определения размера. Например, при ручной доводке детали до заданного геометрического размера рабочий контролирует этот размер с помощью штангенциркуля и прекращает доводку при полном совпадении штрихов, соответствующих заданному размеру. Выбор штангенциркуля обусловлен тем, что предельная погрешность измерения меньше или равна заданному допуску. Другой пример: при отчуждении товаров в единицах массы, объема или длины допустимое предельное отклонение от номинального размера устанавливается соглашением сторон или в законодательном порядке. Предельная погрешность измерительного устройства для «отмеривания» товара должна быть меньше или равна заданному допустимому отклонению. Заметим, что здесь практически совпадают понятия «допускаемая погрешность измерения» и «допускаемое отклонение от размера величины». Во втором случае с помощью измерения проверяют, находится ли размер измеряемой величины в заданном интервале (в поле допуска), например при приемочном контроле изделий по геометрическим размерам. При этом изменение (исправление) размера в процессе измерения невозможно. Результат измерения используется только для определения пригодности. При этом погрешность измерения влияет на окончательные результаты приемки («годен» или «брак») только тех изделий, фактические размеры которых находятся близко к границам поля допуска. Увеличение погрешности измерения увеличивает вероятность того, что часть изделий будет неправильно принята (ошибка 1-го рода), а часть изделия – неправильно забракована (ошибка 2-го рода). На рис. 3.7 показано влияние погрешности измерения на результаты контроля при размерах изделий, близких к границам поля допуска. Если размер изделия находится в поле допуска на расстоянии Влияние погрешности измерения на результаты контроля (разбраковки) оценивается следующими параметрами: т — число деталей в процентах от общего числа, имеющих отклонения за обе границы допуска и принятых в число годных; п — число деталей в процентах от общего числа, имеющих отклонение в пределах допуска и неправильно забракованных; С — вероятностная предельная величина выхода размера за каждую границу допуска у неправильно принятых изделий.
Рис. 3.7. Влияние погрешности измерения на результаты контроля:
Для практического применения построены графики, позволяющие определять параметры разбраковки т, п, С в зависимости от законов распределения и числовых значений погрешностей измерения и изготовления. Для использования графиков предварительно вычисляют следующие параметры: • относительную погрешность измерения (в процентах):
• среднее квадратическое отклонение погрешности измерения:
• среднее квадратическое относительной погрешности измерения:
• среднее квадратическое отклонение технологического рассеивания размеров изделий:
Пример. Определить результаты разбраковки. Дано: 1Т= 20 мм;
Вычисляем необходимые параметры:
Затем для
В рассмотренном примере предельная погрешность измерения составляет 30 % от заданного допуска. При этом получены вполне приемлемые для производственной практики значения параметров т, п, С. Увеличение предельной погрешности до 50 % от допуска в данном случае приведет к увеличению параметров т и п до значений соответственно 1,2 и 6,4% (условно назовем их неприемлемыми). Исходя из приемлемости указанных параметров. Как правило, и осуществляется выбор средств измерений. При линейно-угловых измерениях допустимая предельная погрешность измерений принимается в диапазоне 20...35% от заданного допуска на измеряемый размер, а при арбитражной перепроверке принятых изделий предельная погрешность измерения должна составлять не более 30 % от предельной погрешности, имевшей место при первичной разбраковке. Если недопустимо попадание бракованных изделий в число принятых, то прибегают к производственному допуску, уменьшая размер заданного допуска на величину предельной погрешности измерения или на удвоенную величину параметра С. Введение производственных допусков, так же как и выбор рабочих средств измерений для разбраковки, необходимо осуществлять на основе технико-экономических расчетов. Иногда более экономичным оказывается использование для разбраковки простоте и надежного средства измерений с большой предельной погрешностью, но с перепроверкой забракованных изделий более точным средством измерений или путем повторных многократных измерений. Если область технологического рассеивания размеров изделий практически совпадает с заданным допуском, то приемочный контроль используют для обнаружения возникших нарушений в технологическом цикле. В этом случае все первоначально забракованные изделия подвергают повторному, более тщательному, контролю, и если брак подтверждается, то это свидетельствует о возникших нарушениях в технологическом цикле. Особое внимание уделяется выбору разрядных эталонных средств измерений, используемых при поверочных работах. Если поверяемое средство измерений предназначено для применения без поправок, то в ходе поверки определяют, не выходят ли его погрешности за установленные (допускаемые) пределы. В этой случае результаты поверки можно охарактеризовать параметрами аналогичными рассмотренному случаю разбраковки изделий, и вероятность ошибок 1-го и 2-го рода зависит от отношения погрешностей поверяемого и используемого для поверки средств измерений. Данное отношение для различных видов измерений и различных ступеней поверочных схем колеблется от 1:10 до 1:3 и принимается с учетом всего комплекса метрологических характеристик используемых эталонных средств измерений. Контрольные вопросы для самопроверки.
1. Что такое физическая величина? 2. Сформулируйте понятие единицы и значение физической величины. 3. Понятие измерений и их виды. 4. Понятие о точном измерении. 5. В чем состоит назначение эталона единицы физической величины? 6. В чем заключается поверка средств измерений? 7. Назовите основные единицы системы СИ. 8. Назовите производные единицы системы СИ, используемые при расчетах строительных конструкций. 9. Изобразите принцип построения поверочных схем. 10. В чем заключается калибровка средств измерений? 11. Понятие случайной погрешности. 12. Понятие систематической погрешности. 13. В чем заключается суммирование погрешностей измерений? 14. Что означает понятие о классе точности средств измерений? 15. В чем состоит задача выбора средств измерений? РАЗДЕЛ 2. КОНТРОЛЬ КАЧЕСТВА КОНСТРУКЦИЙ И МАТЕРИАЛОВ.
ЛЕКЦИЯ 4. СИСТЕМА КОНТРОЛЯ КАЧЕСТВА. ВИДЫ И МЕТОДЫ КОНТРОЛЯ
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 5153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.009 с.) |

 результирующей погрешности по известным
результирующей погрешности по известным  составляющих погрешностей. При этом используют ряд упрощений и допущений. Мы приведем лишь основные формулы и правила, которые могут найти применение в строительной практике.
составляющих погрешностей. При этом используют ряд упрощений и допущений. Мы приведем лишь основные формулы и правила, которые могут найти применение в строительной практике. (например, большой длины по частям). Если при этом систематические погрешности при измерениях исключены и коэффициент корреляции между составляющими погрешностями отсутствует, то можно утверждать, что
(например, большой длины по частям). Если при этом систематические погрешности при измерениях исключены и коэффициент корреляции между составляющими погрешностями отсутствует, то можно утверждать, что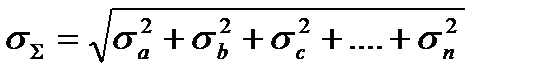
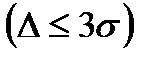 , и при измерениях не вносятся дополнительные методические погрешности, то справедлива формула:
, и при измерениях не вносятся дополнительные методические погрешности, то справедлива формула:

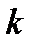 — безразмерный коэффициент.
— безразмерный коэффициент.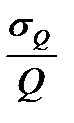
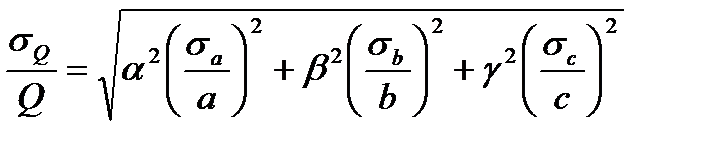 .
.
 в три раза меньше, чем
в три раза меньше, чем  любой из оставляемых погрешностей.
любой из оставляемых погрешностей. . При этом класс точности обозначается одной арабской цифрой (порядковым номером): 0; 1; 2. Наименьшие погрешности соответствуют классу 0. Значения этих погрешностей для разных номинальных значений мер указаны в таблицах стандартов.
. При этом класс точности обозначается одной арабской цифрой (порядковым номером): 0; 1; 2. Наименьшие погрешности соответствуют классу 0. Значения этих погрешностей для разных номинальных значений мер указаны в таблицах стандартов.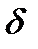 , то класс точности обозначается в виде 1,0, где 1,0 — значение допустимой предельной относительной погрешности в процентах от измеренного значения. Например, если при выполнении измерения прибором, имеющим на щитке обозначение 1,5 получен результат 200, то абсолютная погрешность
, то класс точности обозначается в виде 1,0, где 1,0 — значение допустимой предельной относительной погрешности в процентах от измеренного значения. Например, если при выполнении измерения прибором, имеющим на щитке обозначение 1,5 получен результат 200, то абсолютная погрешность 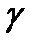 , измеряемой в процентах:
, измеряемой в процентах: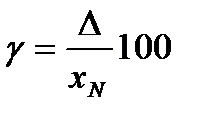
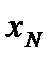 — нормирующее значение, в качестве которого принимается, как правило, значение верхнего предела измерений.
— нормирующее значение, в качестве которого принимается, как правило, значение верхнего предела измерений.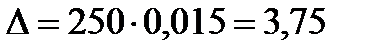 , а относительная погрешность измерения, %, составит:
, а относительная погрешность измерения, %, составит: 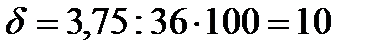 . Для приборов с нормируемой приведенной погрешностью абсолютная погрешность не зависит от значения измеряемой величины, а относительная погрешность увеличивается с уменьшением значения измеряемой величины. Значение абсолютной погрешности можно снизить, если использовать прибор того же класса точности, но с меньшим диапазоном измерений.
. Для приборов с нормируемой приведенной погрешностью абсолютная погрешность не зависит от значения измеряемой величины, а относительная погрешность увеличивается с уменьшением значения измеряемой величины. Значение абсолютной погрешности можно снизить, если использовать прибор того же класса точности, но с меньшим диапазоном измерений.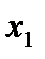 от границы, но при измерении имела место погрешность
от границы, но при измерении имела место погрешность 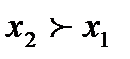 , то изделие будет неправильно забраковано. Аналогично при
, то изделие будет неправильно забраковано. Аналогично при 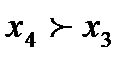 — бракованное изделие будет неправильно принято.
— бракованное изделие будет неправильно принято.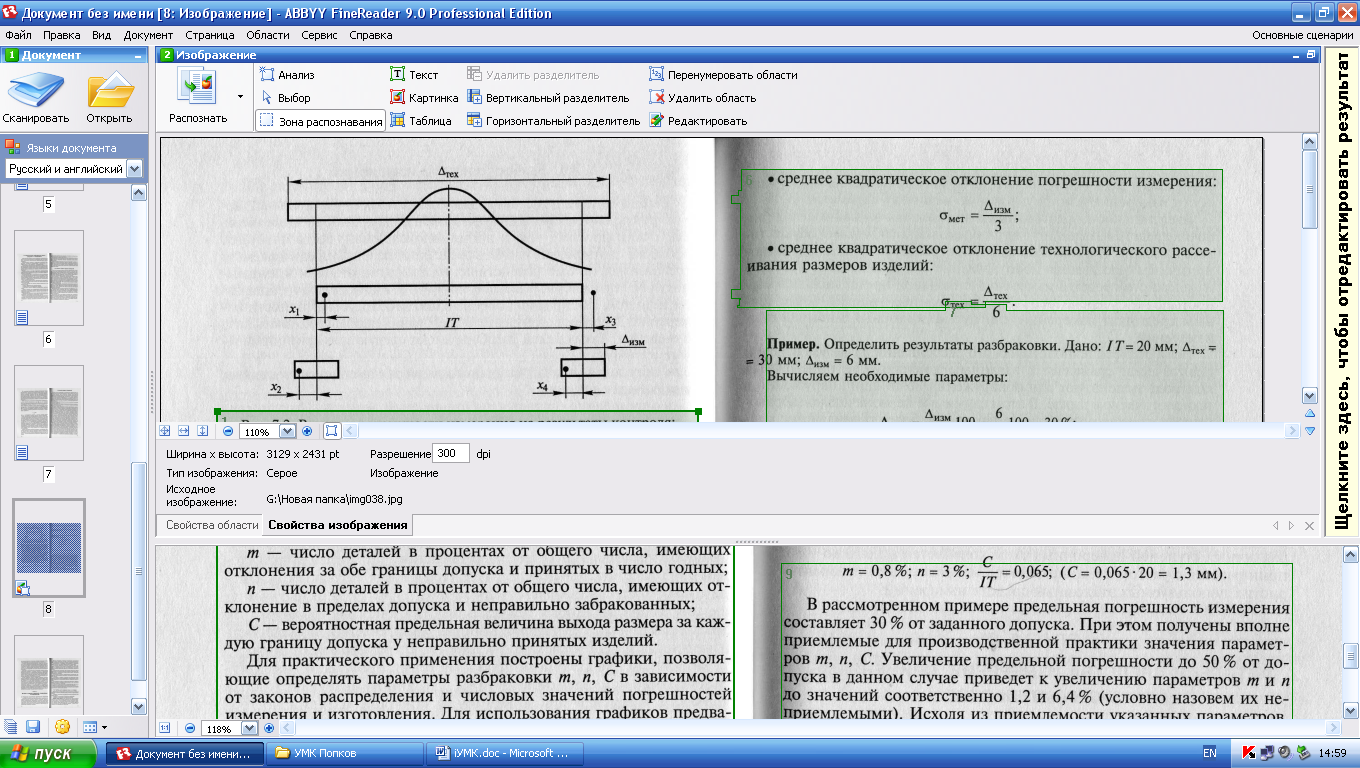
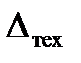 — область технологического рассеивания размеров изделий;
— область технологического рассеивания размеров изделий; 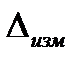 — предельная погрешность измерения; IT — допуск на контролируемый размер;
— предельная погрешность измерения; IT — допуск на контролируемый размер; 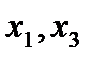 — погрешности изготовления;
— погрешности изготовления; 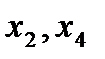 — погрешности измерения
— погрешности измерения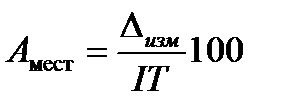 ;
;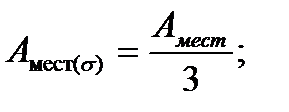
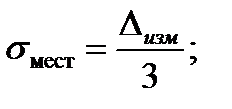
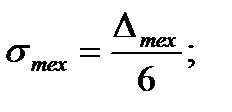
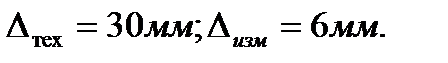
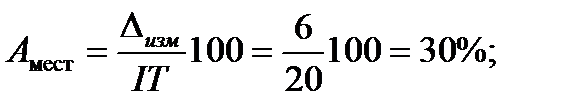
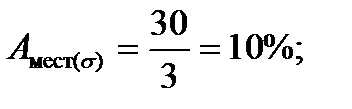
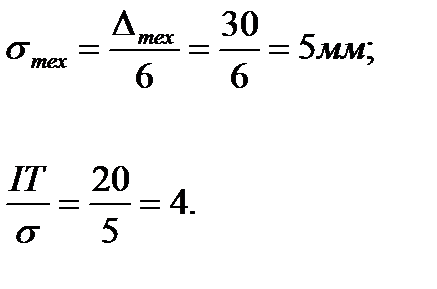
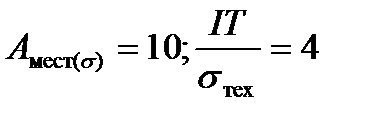 по графикам находим:
по графикам находим: