Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрология и контроль качества в строительствеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ю.В. Попков, А.А. КовАЛЕНКО Виды занятий и формы контроля знаний
3. Тематический план лекционного курса
Итого: 16 часов 4. Тематический план лабораторных занятий
5. Рейтинговая система контроля успешности обучения студентов Суть рейтингового контроля заключается в том, что учебная деятельность каждого студента по всем ее видам и на всех ее этапах оценивается в баллах, которые по определенным правилам объединяются в суммарный показатель – рейтинг студента. Рейтинговая система разработана в соответствии с Положением о рейтинговой системе контроля успешности обучения студентов в ПГУ, одобренном 25 марта 2005г. и утвержденном приказом №123 от 3 мая 2005г. Рейтинг студентов по дисциплине «Метрология и контроль качества в строительстве» определяется суммой баллов, заработанных студентом. Успешность изучения дисциплины слагается из следующих критериев: -отношение к изучению дисциплины (отсутствие пропусков учебных занятий без уважительных причин, добросовестность отношения, своевременность выполнения лабораторных работ. Добросовестное отношение студента оценивается в 250 баллов, в том числе 50 баллов за 100%-ное посещение лекций, 50 балов за 100%-ное посещение лабораторных занятий и 150 баллов за активную работу на них, своевременность выполнения работ; - уровень знаний и умений (устанавливается на лабораторных занятиях по результатам тестирования). Наивысшая оценка по результатам тестирования составляет 250 баллов. Изучение теоретического курса считается успешным, если количество набранных при тестировании баллов составляет 200 и более. Наивысшая оценка по каждой лабораторной работе составляет 100 баллов. Выполнение лабораторных работ считается успешным, если студент выполняет задание каждой контрольной работы на 75% и более; - творческая активность (предполагается участие в Республиканском конкурсе студенческих научных работ по дисциплине, в студенческих конференциях, наличие научных публикаций). Наивысшая оценка за творческую активность составляет 1000 баллов. Конкретная оценка в зависимости от уровня творческих достижений устанавливается преподавателем; -результаты итогового контроля (зачёт). Зачёт включает 2 вопроса. Наивысшая оценка – 700 баллов, в том числе 350 баллов за ответ на каждый вопрос. Сумма баллов, заработанных студентом в течение семестра и на зачёте, образует рейтинг обучения по дисциплине «Метрология и контроль качества в строительстве». Изучение дисциплины считается успешным, если рейтинг составляет 600 баллов и более. Перевод рейтинга обучения студента в официальную систему оценок осуществляется согласно следующей шкале перевода (рейтинг-лист):
КУРС ЛЕКЦИЙ
РАЗДЕЛ 1. МЕТРОЛОГИЯ – НАУКА ОБ ИЗМЕРЕНИЯХ. Международная система единиц физическИХ величин
ЛЕКЦИЯ 1. ОСНОВЫ МЕТРОЛОГИИ Предмет и задачи метрологии
Метрология — наука об измерениях, об обеспечении их единства, о методах и средствах достижения требуемой точности. Метрология является теоретической основой измерительной техники. Для выполнения измерений используется измерительная техника, начиная от простейших измерительных средств и кончая сложными измерительными комплексами, позволяющими измерять физические величины с наивысшей точностью. Точные измерения неоднократно позволяли делать фундаментальные открытия. Повышение точности, расширение диапазонов измерений, повышение быстродействия измерительной аппаратуры позволяют измерять то, что ранее было неизмеримо, и стимулировать появление и развитие новых направлений в науке и технике. В свою очередь, решение научных проблем часто открывает новые пути совершенствования измерений. Оценивая роль метрологии в научно-техническом прогрессе, можно сказать, что чем крупнее научная и техническая проблема, тем большую роль в ее решении играет метрология. В строительстве, начиная с производства строительных материалов и кончая возведением зданий и сооружений, используются измерения различных видов. Измеряют массу и плотность, силу и давление, температуру, параметры электрического тока и другие физические величины. Для измерения основных физических величин используют стандартные измерительные средства с известными метрологическими характеристиками и отработанной организацией поверочных работ. Применяемые измерительные средства имеют, как правило, некоторый запас по точности, т. е. погрешность измерения в 5... 10, а иногда в 20...30 раз меньше, чем заданный допуск на измеряемый параметр. При определении наиболее ответственных функциональных параметров, например прочности бетона при разрушении контрольных кубов, учитываются возможные отклонения от значений, полученных при испытании. Область технологического рассеивания результатов здесь изучена хорошо. Погрешность стандартного измерительного средства (пресса) ничтожно мала по сравнению с рассеиванием, связанным с неоднородностью материала, и не учитывается при расчете гарантированной прочности.
1.2. Основные метрологические параметры и термины.
Физическая величина.
Термин — слово, имеющее специализированное точно ограниченное научное значение. При этом в разных отраслях один и тот же термин может иметь различные значения. Поскольку метрология граничит со всеми отраслями, вопросам терминологии уделяется особое внимание. Установление единства понимания и толкования наиболее общих терминов позволяет избежать ошибок и искажений терминологического характера. Физическая величина — свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Так, все физические тела имеют массу, длину, температуру, но у каждого из них размеры этих физических величин различны. Часто термином «величина» пытаются выразить размер или значение физической величины. Например, говорят: «величина давления», «величина скорости», что, конечно, неправильно. Следует понимать также, что термин «величина» применим только в отношении тех свойств, которые можно оценить количественно. Вместе с тем термин «физическая величина» шире, чем термин «измеряемая величина». В настоящее время под измеряемой величиной понимается параметр или функционал параметра модели объекта измерений, отражающий то его свойство, количественную оценку которого необходимо получить в результате измерения. Измеряемая величина всегда имеет размерность определенной физической величины, но представляет собой некоторую ее конкретизацию, обусловленную поставленной целью измерения. Единица физической величины — размер физической величины, которому по определению придано значение, равное единице. Единица физической величины — такое ее значение, которое принимают за основание для сравнения с ним физических величин того же рода при их количественной оценке. При количественной оценке той или другой физической величины следует употреблять термин «размер». Например: размер давления, размер скорости. Значение физической величины — выражение размера физической величины в виде некоторого числа принятых для ее единиц. Отвлеченное число, входящее в значение величины, называется числовым значением.
Дополнительные единицы СИ
Радиан — угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. Один радиан составляет 57° 17'44,8". Стерадиан — телесный угол, вершина которого расположена в центре сферы и который вырезает на сфере поверхность, площадь которой равна площади квадрата со стороной, по длине равной радиусу сферы. Измеряют телесные углы путем определения плоских углов и проведения дополнительных расчетов по формуле:
где Телесному углу 1 ср соответствует плоский угол, равный 65° 32'; углу Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. На практике плоские углы измеряют, как правило, в угловых градусах, минутах, секундах, которые разрешено использовать наряду с единицами СИ.
Наравне с единицами СИ
Кратные и дольные единицы Наиболее прогрессивным способом образования кратных и дольных единиц является принятая в метрической системе мер десятичная кратность между большими и меньшими единицами. Десятичные кратные и дольные единицы от единиц СИ образуются путем присоединения приставок, взятых из латинского, греческого и датского языков. Множители и приставки для образования десятичных кратных и дольных единиц в СИ и их обозначения приведены в табл. 2.6.
Таблица 2.6 Множители и приставки для образования Значения функции Лапласа
В интервале В производственной практике часто считается необходимым выполнение следующего условия: допустимое предельное отклонение от заданного номинального размера должно быть не меньше интервала Область технологического рассеивания какого-либо размера (параметра) изделия, как правило, подчиняется нормальному закону, и периодически определяемое среднее квадратическое отклонение является показателем изменений в технологическом цикле. Значения функции Стьюдента для интервалов t=2...3,5
3.5. Критерии оценки грубых погрешностей (промахов) При однократных измерениях обнаружить грубую погрешность не всегда удается. При многократных измерениях для их обнаружения используют статистические критерии. При этом задаются вероятностью При числе наблюдений При малом числе наблюдений Таблица 3.4 Значения критерия Романовского Выбор средств измерений Учет всего комплекса метрологических характеристик необходим только при измерениях высокой точности, а также при проектировании сложных измерительных систем. В большинстве производственных отраслей, в том числе в строительстве, используют рабочие средства измерений, метрологические характеристики которых нормированы на основе классов точности. Класс точности — обобщенная характеристика средств измерений определенного типа, позволяющая судить о том, в каком диапазоне находится суммарная погрешность измерений. Совокупность метрологических характеристик, определяющих класс точности, отражается в стандартах или технических условиях. Средствам измерений с несколькими диапазонами измерений одной и той же физической величины или предназначенным для измерений разных физических величин могут быть присвоены различные классы точности для каждого диапазона или каждой измеряемой величины. Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений. При этом в эксплуатационной документации на средства измерений, содержащей обозначение класса точности, должна быть ссылка на стандарт или технические условия, в которых установлен класс точности для этого типа средств измерений. Обозначения могут иметь форму заглавных букв латинского алфавита или римских цифр с добавлением условных знаков. Смысл таких обозначений раскрывается в нормативно-технической документации. Если же класс точности обозначается арабскими цифрами с добавлением какого-либо знака, то эти цифры непосредственно оценивают погрешность измерения. Для выражения допускаемых основных погрешностей при их нормировании и оценке используют различные способы, в зависимости от того, какой из них наиболее соответствует характеру средства измерений. Например, для гирь, штангенинструмента, концевых мер длины указывают значения абсолютных допускаемых погрешностей Если нормируется допустимая относительная погрешность
где Класс точности при этом обозначается числом из того же ряда, что и при нормировании относительной погрешности, но дополнительного значка при этом нет. Например, если вольтметр класса 1,5 с диапазоном измерений от 0 до 250 В показывает напряжение 36 В, то абсолютная погрешность измерения, В, составит: Шкалы некоторых приборов градуируют в миллиметрах, абсолютная погрешность при этом выражается также в единицах длины. Если для такого прибора нормируется значение приведенной погрешности, то класс точности прибора обозначается в виде 1,0, где 1,0 — значение приведенной погрешности, выраженное в процентах. Выбор средств измерений для конкретных измерительных целей определяется многими факторами. Задача выбора может быть как очень простой, так и достаточно сложной, когда требуется проверка соответствия свойств средства измерения предъявляемым требованиям по быстродействию, надежности, степени защищенности от определенных воздействий и т. п. Но главным требованием является, как правило, обеспечение необходимой точности измерений. Для обоснования этого требования необходимо знать цель измерения. Таких целей две. Они имеют следующие принципиальные отличия: • определение действительного размера измеряемой величины в заданных единицах; • определение соответствия измеряемой величины предписанному (номинальному) размеру, для которого заданы допустимые предельные отклонения. В первом случае измеряемой величине присваивается размер, достоверность которого полностью определяется погрешностью, имевшей место в момент измерения. Допустимая погрешность назначается исходя из конкретных задач определения размера. Например, при ручной доводке детали до заданного геометрического размера рабочий контролирует этот размер с помощью штангенциркуля и прекращает доводку при полном совпадении штрихов, соответствующих заданному размеру. Выбор штангенциркуля обусловлен тем, что предельная погрешность измерения меньше или равна заданному допуску. Другой пример: при отчуждении товаров в единицах массы, объема или длины допустимое предельное отклонение от номинального размера устанавливается соглашением сторон или в законодательном порядке. Предельная погрешность измерительного устройства для «отмеривания» товара должна быть меньше или равна заданному допустимому отклонению. Заметим, что здесь практически совпадают понятия «допускаемая погрешность измерения» и «допускаемое отклонение от размера величины». Во втором случае с помощью измерения проверяют, находится ли размер измеряемой величины в заданном интервале (в поле допуска), например при приемочном контроле изделий по геометрическим размерам. При этом изменение (исправление) размера в процессе измерения невозможно. Результат измерения используется только для определения пригодности. При этом погрешность измерения влияет на окончательные результаты приемки («годен» или «брак») только тех изделий, фактические размеры которых находятся близко к границам поля допуска. Увеличение погрешности измерения увеличивает вероятность того, что часть изделий будет неправильно принята (ошибка 1-го рода), а часть изделия – неправильно забракована (ошибка 2-го рода). На рис. 3.7 показано влияние погрешности измерения на результаты контроля при размерах изделий, близких к границам поля допуска. Если размер изделия находится в поле допуска на расстоянии Влияние погрешности измерения на результаты контроля (разбраковки) оценивается следующими параметрами: т — число деталей в процентах от общего числа, имеющих отклонения за обе границы допуска и принятых в число годных; п — число деталей в процентах от общего числа, имеющих отклонение в пределах допуска и неправильно забракованных; С — вероятностная предельная величина выхода размера за каждую границу допуска у неправильно принятых изделий.
Рис. 3.7. Влияние погрешности измерения на результаты контроля:
Для практического применения построены графики, позволяющие определять параметры разбраковки т, п, С в зависимости от законов распределения и числовых значений погрешностей измерения и изготовления. Для использования графиков предварительно вычисляют следующие параметры: • относительную погрешность измерения (в процентах):
• среднее квадратическое отклонение погрешности измерения:
• среднее квадратическое относительной погрешности измерения:
• среднее квадратическое отклонение технологического рассеивания размеров изделий:
Пример. Определить результаты разбраковки. Дано: 1Т= 20 мм;
Вычисляем необходимые параметры:
Затем для
В рассмотренном примере предельная погрешность измерения составляет 30 % от заданного допуска. При этом получены вполне приемлемые для производственной практики значения параметров т, п, С. Увеличение предельной погрешности до 50 % от допуска в данном случае приведет к увеличению параметров т и п до значений соответственно 1,2 и 6,4% (условно назовем их неприемлемыми). Исходя из приемлемости указанных параметров. Как правило, и осуществляется выбор средств измерений. При линейно-угловых измерениях допустимая предельная погрешность измерений принимается в диапазоне 20...35% от заданного допуска на измеряемый размер, а при арбитражной перепроверке принятых изделий предельная погрешность измерения должна составлять не более 30 % от предельной погрешности, имевшей место при первичной разбраковке. Если недопустимо попадание бракованных изделий в число принятых, то прибегают к производственному допуску, уменьшая размер заданного допуска на величину предельной погрешности измерения или на удвоенную величину параметра С. Введение производственных допусков, так же как и выбор рабочих средств измерений для разбраковки, необходимо осуществлять на основе технико-экономических расчетов. Иногда более экономичным оказывается использование для разбраковки простоте и надежного средства измерений с большой предельной погрешностью, но с перепроверкой забракованных изделий более точным средством измерений или путем повторных многократных измерений. Если область технологического рассеивания размеров изделий практически совпадает с заданным допуском, то приемочный контроль используют для обнаружения возникших нарушений в технологическом цикле. В этом случае все первоначально забракованные изделия подвергают повторному, более тщательному, контролю, и если брак подтверждается, то это свидетельствует о возникших нарушениях в технологическом цикле. Особое внимание уделяется выбору разрядных эталонных средств измерений, используемых при поверочных работах. Если поверяемое средство измерений предназначено для применения без поправок, то в ходе поверки определяют, не выходят ли его погрешности за установленные (допускаемые) пределы. В этой случае результаты поверки можно охарактеризовать параметрами аналогичными рассмотренному случаю разбраковки изделий, и вероятность ошибок 1-го и 2-го рода зависит от отношения погрешностей поверяемого и используемого для поверки средств измерений. Данное отношение для различных видов измерений и различных ступеней поверочных схем колеблется от 1:10 до 1:3 и принимается с учетом всего комплекса метрологических характеристик используемых эталонных средств измерений. Контрольные вопросы для самопроверки.
1. Что такое физическая величина? 2. Сформулируйте понятие единицы и значение физической величины. 3. Понятие измерений и их виды. 4. Понятие о точном измерении. 5. В чем состоит назначение эталона единицы физической величины? 6. В чем заключается поверка средств измерений? 7. Назовите основные единицы системы СИ. 8. Назовите производные единицы системы СИ, используемые при расчетах строительных конструкций. 9. Изобразите принцип построения поверочных схем. 10. В чем заключается калибровка средств измерений? 11. Понятие случайной погрешности. 12. Понятие систематической погрешности. 13. В чем заключается суммирование погрешностей измерений? 14. Что означает понятие о классе точности средств измерений? 15. В чем состоит задача выбора средств измерений? РАЗДЕЛ 2. КОНТРОЛЬ КАЧЕСТВА КОНСТРУКЦИЙ И МАТЕРИАЛОВ.
ЛЕКЦИЯ 4. СИСТЕМА КОНТРОЛЯ КАЧЕСТВА. ВИДЫ И МЕТОДЫ КОНТРОЛЯ Механические методы. Метод определения прочности путем измерения пластической деформации основан на зависимости между пределом прочности материала и размерами отпечатка на поверхности элемента, полученного при вдавливании индентора статическим или динамическим воздействием. При статическом загружении возрастающая нагрузка на индентор прикладывается плавно. При динамическом загружении применяется метод ударного вдавливания стального шарика или диска. Эти методы детально разработаны в технологии металлов для определения временного сопротивления стали по ее, твердости по Бринеллю, Роквеллу или Виккерсу (рис. 5.2).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

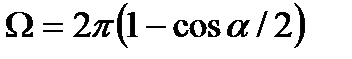 ,
,
 — телесный угол;
— телесный угол; 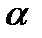 — плоский угол при вершине конуса, образованного внутри сферы данным телесным углом.
— плоский угол при вершине конуса, образованного внутри сферы данным телесным углом.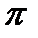 ср — плоский угол, равный 120°; углу 2
ср — плоский угол, равный 120°; углу 2 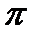 ср — плоский угол, равный 180°.
ср — плоский угол, равный 180°.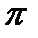 /180) рад = 1,745329·10-2 рад
(
/180) рад = 1,745329·10-2 рад
(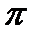 /10 800) рад = 2,908882·
10-4рад
(
/10 800) рад = 2,908882·
10-4рад
(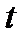
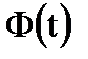
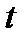
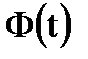
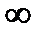
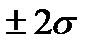 погрешность находится с вероятностью ≈ 0,95 (0,4772·2), в интервале
погрешность находится с вероятностью ≈ 0,95 (0,4772·2), в интервале 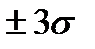 — с вероятностью 0,9973, т.е. вероятность того, что случайная погрешность не выйдет за пределы
— с вероятностью 0,9973, т.е. вероятность того, что случайная погрешность не выйдет за пределы 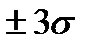 , составляет 0,9973, или 99,73 %. На практике с учетом интервала
, составляет 0,9973, или 99,73 %. На практике с учетом интервала  при числе измерений n от 2 до 20
при числе измерений n от 2 до 20 (уровнем значимости) того, что сомнительный результат действительно может иметь место в данной совокупности результатов измерений.
(уровнем значимости) того, что сомнительный результат действительно может иметь место в данной совокупности результатов измерений. используют, как правило, критерий трех сигм (критерий Райта). По этому критерию промахом считается результат наблюдения
используют, как правило, критерий трех сигм (критерий Райта). По этому критерию промахом считается результат наблюдения  который отличается от среднего
который отличается от среднего  более чем на
более чем на  , т.е.
, т.е. 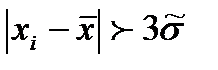 . Вероятность возникновения такого результата
. Вероятность возникновения такого результата  (1 - 0,9973).
(1 - 0,9973). применяют критерий Романовского. При этом вычисляют отношение
применяют критерий Романовского. При этом вычисляют отношение  и сравнивают его с критерием
и сравнивают его с критерием  , зависящим от заданного уровня значимости
, зависящим от заданного уровня значимости  и числа наблюдений
и числа наблюдений  (табл. 3.4). При
(табл. 3.4). При  результат считается промахом и отбрасывается.
результат считается промахом и отбрасывается.
 . При этом класс точности обозначается одной арабской цифрой (порядковым номером): 0; 1; 2. Наименьшие погрешности соответствуют классу 0. Значения этих погрешностей для разных номинальных значений мер указаны в таблицах стандартов.
. При этом класс точности обозначается одной арабской цифрой (порядковым номером): 0; 1; 2. Наименьшие погрешности соответствуют классу 0. Значения этих погрешностей для разных номинальных значений мер указаны в таблицах стандартов.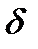 , то класс точности обозначается в виде 1,0, где 1,0 — значение допустимой предельной относительной погрешности в процентах от измеренного значения. Например, если при выполнении измерения прибором, имеющим на щитке обозначение 1,5 получен результат 200, то абсолютная погрешность
, то класс точности обозначается в виде 1,0, где 1,0 — значение допустимой предельной относительной погрешности в процентах от измеренного значения. Например, если при выполнении измерения прибором, имеющим на щитке обозначение 1,5 получен результат 200, то абсолютная погрешность 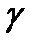 , измеряемой в процентах:
, измеряемой в процентах: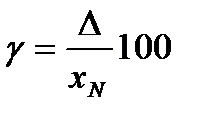
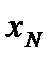 — нормирующее значение, в качестве которого принимается, как правило, значение верхнего предела измерений.
— нормирующее значение, в качестве которого принимается, как правило, значение верхнего предела измерений.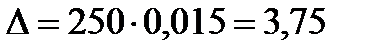 , а относительная погрешность измерения, %, составит:
, а относительная погрешность измерения, %, составит: 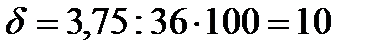 . Для приборов с нормируемой приведенной погрешностью абсолютная погрешность не зависит от значения измеряемой величины, а относительная погрешность увеличивается с уменьшением значения измеряемой величины. Значение абсолютной погрешности можно снизить, если использовать прибор того же класса точности, но с меньшим диапазоном измерений.
. Для приборов с нормируемой приведенной погрешностью абсолютная погрешность не зависит от значения измеряемой величины, а относительная погрешность увеличивается с уменьшением значения измеряемой величины. Значение абсолютной погрешности можно снизить, если использовать прибор того же класса точности, но с меньшим диапазоном измерений.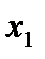 от границы, но при измерении имела место погрешность
от границы, но при измерении имела место погрешность 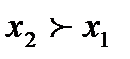 , то изделие будет неправильно забраковано. Аналогично при
, то изделие будет неправильно забраковано. Аналогично при 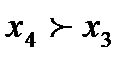 — бракованное изделие будет неправильно принято.
— бракованное изделие будет неправильно принято.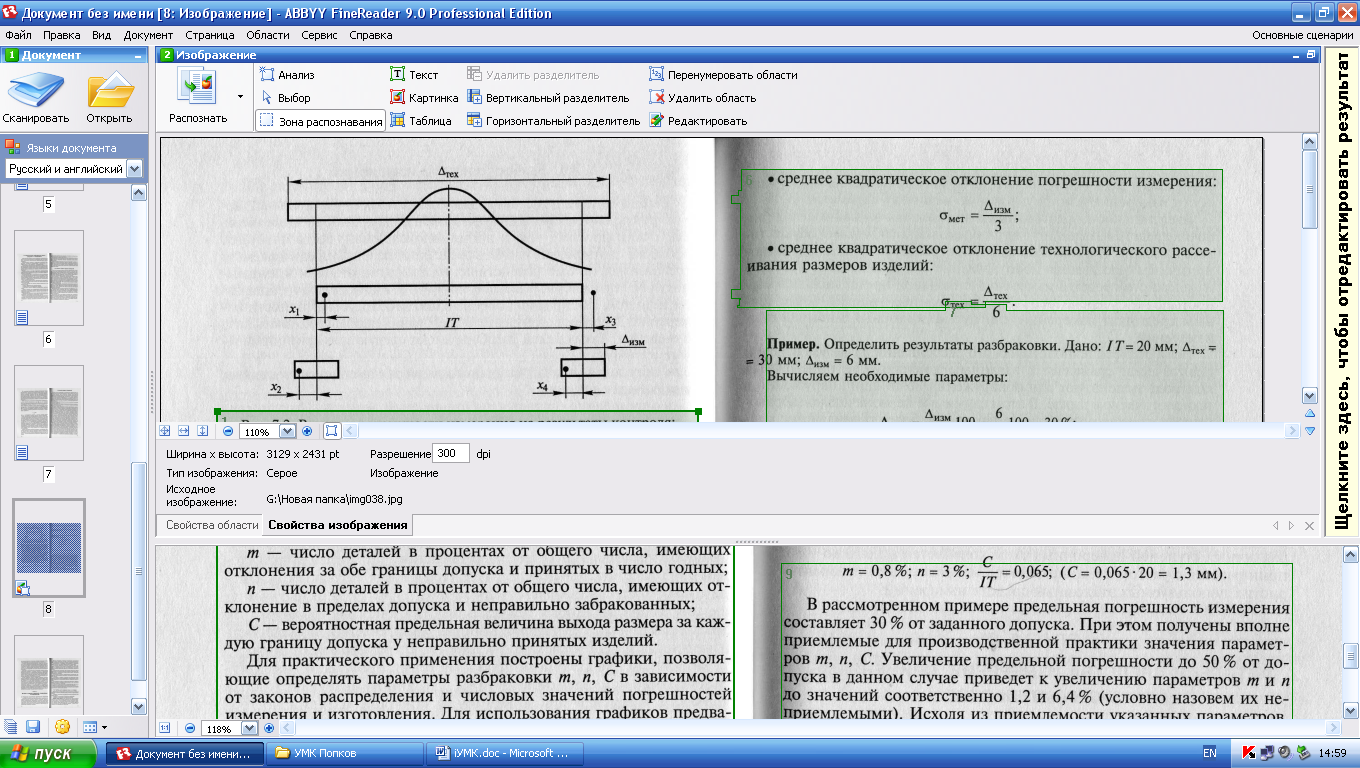
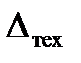 — область технологического рассеивания размеров изделий;
— область технологического рассеивания размеров изделий; 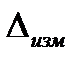 — предельная погрешность измерения; IT — допуск на контролируемый размер;
— предельная погрешность измерения; IT — допуск на контролируемый размер; 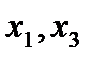 — погрешности изготовления;
— погрешности изготовления; 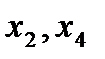 — погрешности измерения
— погрешности измерения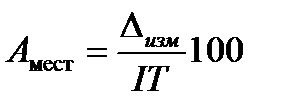 ;
;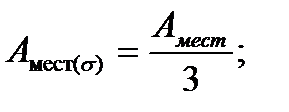
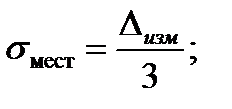
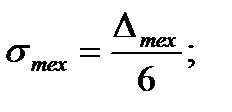
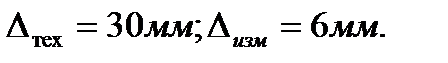
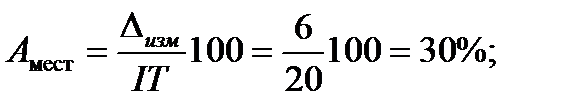
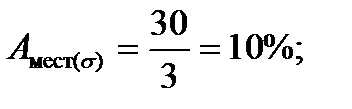
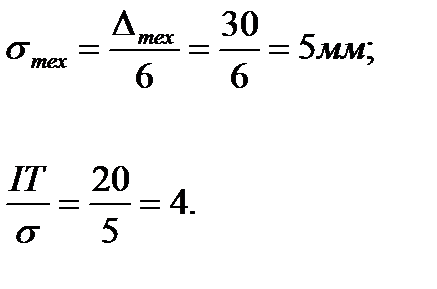
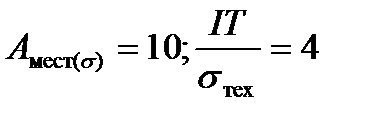 по графикам находим:
по графикам находим: