
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов измерений, содержащих случайные погрешностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На практике приходится довольствоваться ограниченным числом измерений для того, чтобы оценить истинное значение измеряемой величины и точность измерения. Если число измерений велико (более 100), то кривую распределения можно построить достаточно точно, и если она соответствует нормальному закону, то графически определяется математическое ожидание
Примечание: При этом Статистический ряд служит основой для построения гистограммы и статистической функции распределения (рис. 3.5). При Соответствие полученной кривой закону нормального распределения проверяют по критериям Пирсона или Холмогорова. Если измерений меньше 15, то принадлежность экспериментального распределения к нормальному не проверяется.
Рис. 3.5. Построение гистограммы и статистической функции распределения по опытным данным:
При обработке результатов ограниченного числа наблюдений в качестве оценки математического ожидания принимается среднее арифметическое результатов наблюдений:
Приближенное значение среднего квадратического отклонения в этом случае вычисляется по формуле:
Появление в знаменателе выражения Среднее арифметическое отличается от математического ожидания на величину случайной погрешности (погрешности среднего значения), которая подчиняется тому же закону распределения, что и погрешности результатов отдельных наблюдений. Дисперсия среднего арифметического вычисляется по формуле:
а среднее квадратическое среднего арифметического — по формуле:
При увеличении числа наблюдений Границы доверительного интервала, в котором с заданной вероятностью (обеспеченностью) находится случайная погрешность среднего арифметического, определяют по формуле:
При числе наблюдений Зная число наблюдений Таблица 3.2. Значения коэффициента и заданной доверительной вероятности
Таблица 3.3. Значения функции Стьюдента для интервалов t=2...3,5
3.5. Критерии оценки грубых погрешностей (промахов) При однократных измерениях обнаружить грубую погрешность не всегда удается. При многократных измерениях для их обнаружения используют статистические критерии. При этом задаются вероятностью При числе наблюдений При малом числе наблюдений Таблица 3.4 Значения критерия Романовского
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.41.80 (0.012 с.) |

 и среднее квадратическое отклонение
и среднее квадратическое отклонение  . Результаты измерений
. Результаты измерений  делят на 10...20 интервалов
делят на 10...20 интервалов  и записывают в виде статистического ряда
и записывают в виде статистического ряда





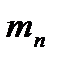




 — число результатов в интервале;
— число результатов в интервале;  — вычисленная вероятность попадания в данный интервал.
— вычисленная вероятность попадания в данный интервал. ;
;  .
. гистограмма переходит в плавную кривую.
гистограмма переходит в плавную кривую.
 — принятый интервал;
— принятый интервал;  — вероятность попадания соответственно в интервалы 1 и 2;
— вероятность попадания соответственно в интервалы 1 и 2;  — ордината функции распределения в точке 1
— ордината функции распределения в точке 1

 вместо п связано с заменой математического ожидания средним арифметическим незначительного числа наблюдений.
вместо п связано с заменой математического ожидания средним арифметическим незначительного числа наблюдений.

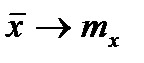 и
и  .
. .
.
 значения коэффициента определяют по таблицам функции Лапласа (см. табл. 3.1), а при
значения коэффициента определяют по таблицам функции Лапласа (см. табл. 3.1), а при  -по таблицам функции Стьюдента (табл. 3.2, 3.3).
-по таблицам функции Стьюдента (табл. 3.2, 3.3). и задавшись доверительной вероятностью
и задавшись доверительной вероятностью  , можно найти по табл. 3.2 значение
, можно найти по табл. 3.2 значение  и, умножив его на
и, умножив его на 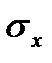 , определить границы доверительного интервала. В тех случаях, когда требуется определить доверительную вероятность при заданном
, определить границы доверительного интервала. В тех случаях, когда требуется определить доверительную вероятность при заданном  при числе измерений
при числе измерений  от 2 до 20
от 2 до 20




 при числе измерений n от 2 до 20
при числе измерений n от 2 до 20 (уровнем значимости) того, что сомнительный результат действительно может иметь место в данной совокупности результатов измерений.
(уровнем значимости) того, что сомнительный результат действительно может иметь место в данной совокупности результатов измерений. используют, как правило, критерий трех сигм (критерий Райта). По этому критерию промахом считается результат наблюдения
используют, как правило, критерий трех сигм (критерий Райта). По этому критерию промахом считается результат наблюдения  который отличается от среднего
который отличается от среднего  более чем на
более чем на  , т.е.
, т.е. 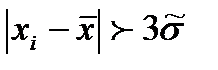 . Вероятность возникновения такого результата
. Вероятность возникновения такого результата  (1 - 0,9973).
(1 - 0,9973). применяют критерий Романовского. При этом вычисляют отношение
применяют критерий Романовского. При этом вычисляют отношение  и сравнивают его с критерием
и сравнивают его с критерием  , зависящим от заданного уровня значимости
, зависящим от заданного уровня значимости  и числа наблюдений
и числа наблюдений  (табл. 3.4). При
(табл. 3.4). При  результат считается промахом и отбрасывается.
результат считается промахом и отбрасывается.



