Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение систематических погрешностей.Содержание книги Поиск на нашем сайте 1. Исключение известных систематических погрешностей из результатов наблюдений или измерений выполняем введением поправок к этим результатам. Поправки по абсолютному значению равны этим погрешностям и противоположны им по знаку. 2. Введением поправок исключаем: погрешность, возникающую из-за отклонений действительной температуры окружающей среды при измерении от нормальной; погрешность, возникающую из-за отклонений атмосферного давления при измерении от нормального; погрешность, возникающую из-за отклонений относительной влажности окружающего воздуха при измерении от нормальной; погрешность, возникающую из-за отклонений относительной скорости движения внешней среды при измерении от нормальной; погрешность, возникающую вследствие искривления светового луча (рефракции); погрешность шкалы средства измерения; погрешность, возникающую вследствие несовпадения направлений линии измерения и измеряемого размера. 3. Поправки по указанным погрешностям вычисляем в соответствии с указаниями таблицы. Таблица № 15 Поправки для исключения систематических погрешностей
Продолжение таблица № 15
Обозначения, принятые в таблице: L - непосредственно измеряемый размер, мм; h - величина отклонения направления измерения от направления измеряемого размера, мм; Q - предельное значение допустимой силы ветра, Н; Р - сила натяжения мерного прибора (рулетки, проволоки), Н. 4. Поправки могут не вноситься, если действительная погрешность измерения не превышает предельной. Пример. Определить систематические погрешности и записать результат с учетом различных параметров. Получен результат измерения длины стальной фермы xi = 24003 мм. Измерение выполнялось 3-метровой рулеткой из нержавеющей стали при t = -20 °С. При этом a1 = 20,5·10-6, a2 = 12,5·10-6, t1 = t2 = -20°С, Решение 1. Поправка на температуру окружающей среды Действительную длину xi фермы с учетом поправки на температуру окружающей среды принимаем равной
2. Поправка на относительную скорость внешней среды
Действительную длину xi фермы с учетом поправки на относительную скорость внешней среды принимаем равной
3. Поправка на длину шкалы средства измерения
Действительную длину xi фермы с учетом поправки на длину шкалы средства измерения принимаем равной
4. Поправка на несовпадение направлений линии измерения и измеряемого размера
Действительную длину xi фермы с учетом поправки несовпадение направлений линии измерения и измеряемого размера принимаем равной
Действительную длину xi фермы с учетом всех поправок принимаем равной
Задание
Определить систематические погрешности и записать результат с учетом различных параметров. Данные результатов измерений приведены в таблице №16
Таблица № 16
Задача 3 А) ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА ВИДА РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
Для предварительной оценки вида распределения по полученным данным строят гистограмму распределений или полигон распределения. В начале производится группирование – разделение данных от наименьшего x min до наибольшего x max на r интервалов. Для количества измерений от 30 до 100 рекомендуемое число интервалов – от 7 до 9. Ширину интервала выбирают постоянной для всего ряда данных, при этом следует иметь в виду, что ширина интервала должна быть больше погрешности округления при записи данных. Ширину интервала вычисляют по формуле
Вычисленное значение h обычно округляют. Например при h = 0,0187 это значение округляют до h = 0,02. Установив границы интервалов, подсчитывают число результатов измерений, попавших в каждый интервал. При построении гистограммы или полигона распределения масштаб этих графиков рекомендуется выбирать так, чтобы высота графика относилась к его основанию примерно как 3 к 5. Пример Построить гистограмму и полигон распределения по полученным экспериментальным данным, приведенным в табл. 17. Таблица № 17 Результаты измерений
Определяем ширину интервала
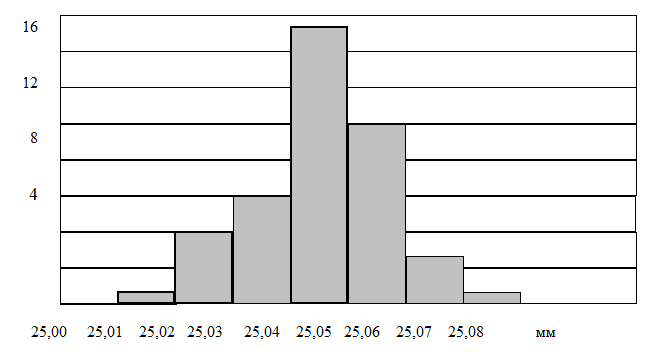
Строим гистограмму распределений (рис. 1), подсчитав число экспериментальных данных, попавших в каждый интервал.
Рис.1. Гистограмма распределений результатов измерений
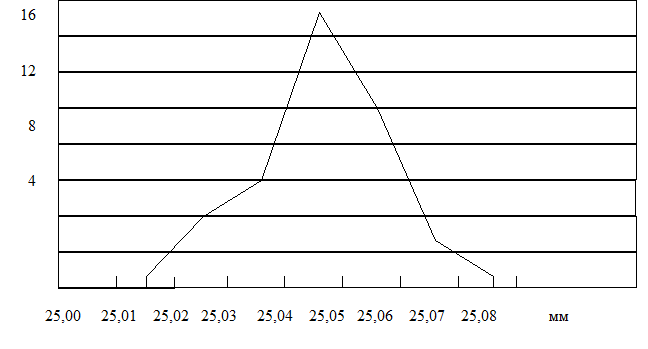
Далее, строим полигон распределения (рис. 2), который представляет собой кусочно-линейную аппроксимацию искомой функции плотности распределения результатов измерения.
Рис. 2. Полигон распределения результатов измерения
Б) ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Нормальный закон распределения, называемый часто распределением Гаусса описывается зависимостью
где σ – параметр рассеивания распределения, равный среднему квадратическому отклонению.
Широкое использование нормального распределения на практике объясняется теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. При количестве измерений n < 10 проверить гипотезу о виде распределения результатов измерения невозможно. При числе данных 10 < n < 50 также трудно судить о виде распределения. Поэтому для проверки соответствия распределения данных нормальному распределению используют составной критерий. Если гипотеза о нормальности отвергается хотя бы по одному из критериев, считают, что распределение результатов измерения отлично от нормального.
Критерий 1. Вычисляют значение d по формуле
где S * – смещенное СКО;
Гипотеза о нормальности подтверждается, если
где
Таблица № 18 Значения процентных точек q для распределения d
Критерий 2. Гипотеза о нормальности распределения результатов измерения подтверждается, если не более m разностей Значения доверительной вероятности P выбирают из табл. 19. Таблица № 19 Значения доверительной вероятности Р
Пример
В табл. 19 приведены результаты измерения угла одним оператором, одним и тем же теодолитом, в одних и тех же условиях. Проверить, можно ли считать, что приведенные в табл. 20 данные принадлежат совокупности, распределенной нормально. Таблица № 20 Результаты исследований
Оценка измеряемой величины равна
Средние квадратические отклонения S и S* найдем по формулам:
Оценка параметра d составит
Уровень значимости критерия 1 примем q = 2%. Из табл. 18 находим d 1% = = 0,92 и d 99% = 0,68. При определении d 1% и d 99% использовалась линейная интерполяция ввиду того, что значение n = 14 в таблице отсутствует. Критерий 1 выполняется, так как Применим критерий 2. Выбрав уровень значимости q = 0,05 для n =14 из табл. 11, найдем Р = 0,97. Из табл. 21 определим zp/2 = 2,17. Тогда
S ∙ zp/2 = 3,245 ∙ 2,17 = 7,042.
Таблица № 21 Значения Р- процентных точек нормированной функции Лапласа
Согласно критерию 2, не более одной разности Следовательно, гипотеза о нормальности распределения данных подтверждается. Уровень значимости составного критерия: q £ 0,02 + 0,05 = 0,07, т. е. гипотеза о нормальности распределения результатов измерения подтверждается при уровне значимости не более 0,07.
Задание
Произвести проверку нормальности распределения измерений по данным приведенным в таблице № 22 и по полученным данным построить гистограмму распределений или полигон распределения. Таблице № 22
Задача 4
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 1751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

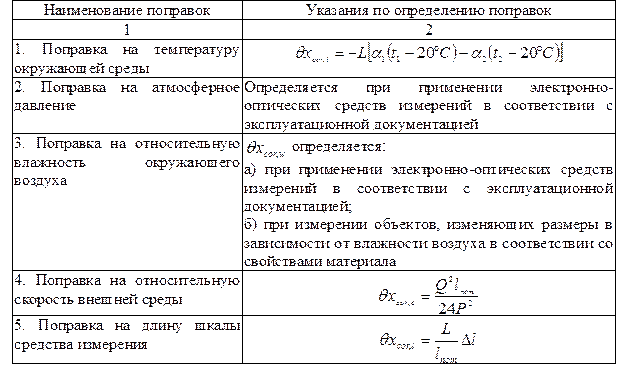
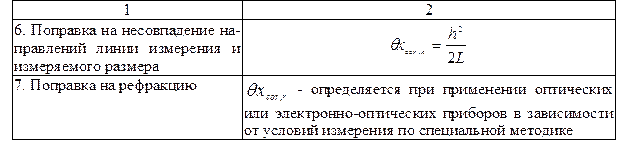
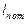 - номинальная длина мерного прибора, мм;
- номинальная длина мерного прибора, мм;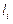 - действительная длина мерного прибора, мм;
- действительная длина мерного прибора, мм;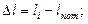
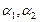 - коэффициенты линейного расширения средства измерения и объекта, 10-6 град-1;
- коэффициенты линейного расширения средства измерения и объекта, 10-6 град-1;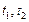 - температура средства измерения и объекта, °С;
- температура средства измерения и объекта, °С;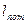 = 3000 мм,
= 3000 мм, 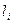 = 3002 мм, h = 35 мм, P = 9 Н, Q = 1,2 Н.
= 3002 мм, h = 35 мм, P = 9 Н, Q = 1,2 Н.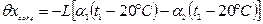 мм.
мм. = -24003[20,5·10-6(-20 - 20) - 12,5·10-6(-20 - 20)]» 7,7 мм.
= -24003[20,5·10-6(-20 - 20) - 12,5·10-6(-20 - 20)]» 7,7 мм.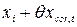 = 24003 + 7,7 = 24010,7 мм.
= 24003 + 7,7 = 24010,7 мм.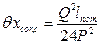 мм.
мм. мм.
мм.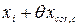 = 24003 + 2,22 = 24002,22 мм.
= 24003 + 2,22 = 24002,22 мм.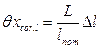 мм.
мм.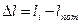 мм.
мм.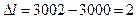 мм.
мм.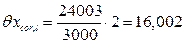 мм.
мм.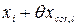 = 24003 + 16,002 = 24019,002 мм.
= 24003 + 16,002 = 24019,002 мм.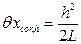 мм.
мм.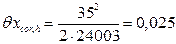 мм.
мм.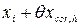 = 24003 + 0,025 = 24003,025 мм.
= 24003 + 0,025 = 24003,025 мм.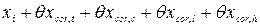 = 24003 + 7,7 + 2,22 + 16,002 + 0,025 = 24028,9 мм.
= 24003 + 7,7 + 2,22 + 16,002 + 0,025 = 24028,9 мм.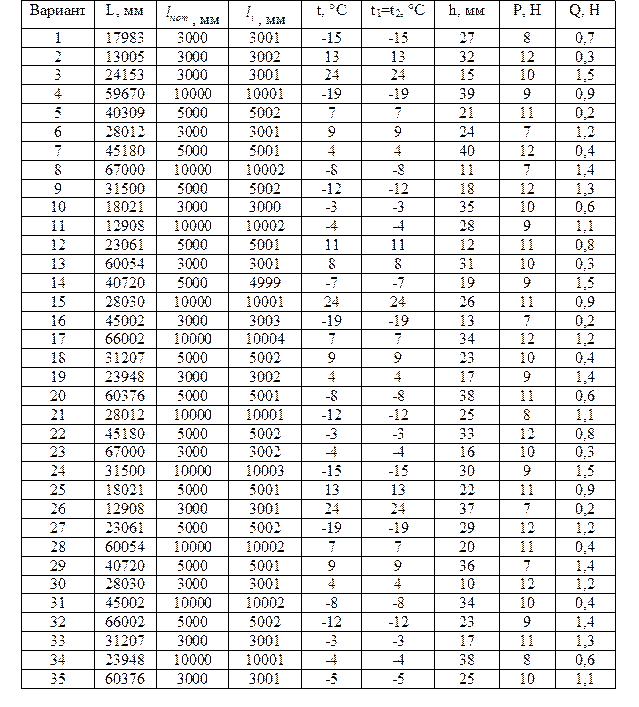
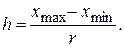
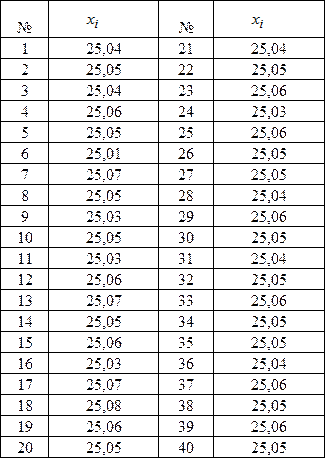

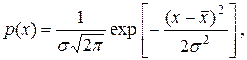
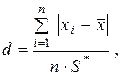
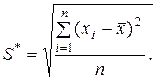
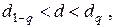
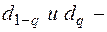 процентные точки распределения значений d, которые находятся по табл. 18.
процентные точки распределения значений d, которые находятся по табл. 18.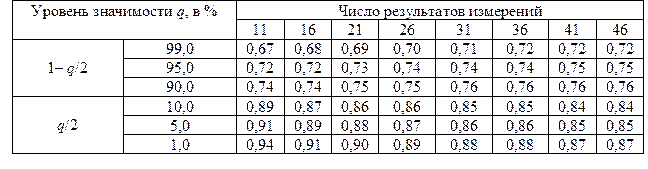
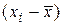 превзошли значения S×zp/2. Здесь
превзошли значения S×zp/2. Здесь 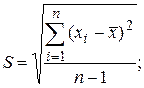 zp/2 – верхняя 100 ∙ P/2 – процентная точка нормированной функции Лапласа
zp/2 – верхняя 100 ∙ P/2 – процентная точка нормированной функции Лапласа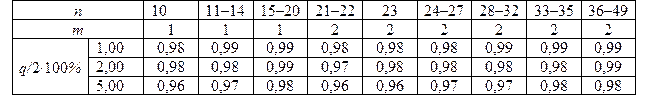
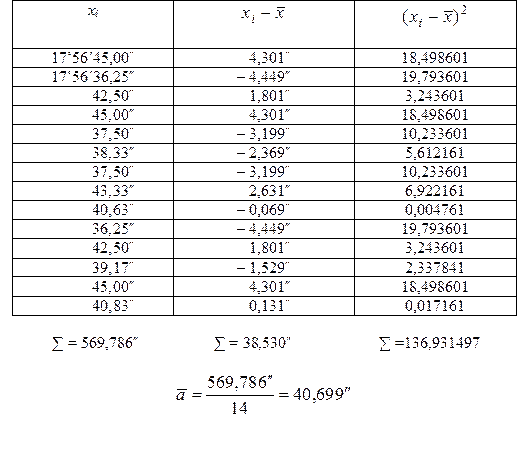
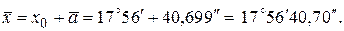
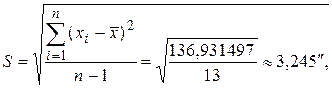
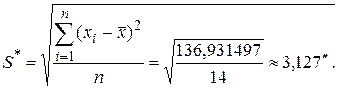
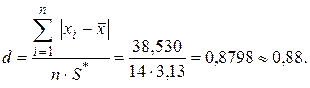
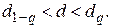 В нашем случае это – 0,68 < 0,88 < 0,92.
В нашем случае это – 0,68 < 0,88 < 0,92.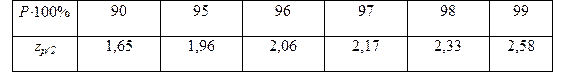
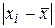 может превзойти 7,042. Из данных табл. 20 следует, что ни одно отклонение
может превзойти 7,042. Из данных табл. 20 следует, что ни одно отклонение