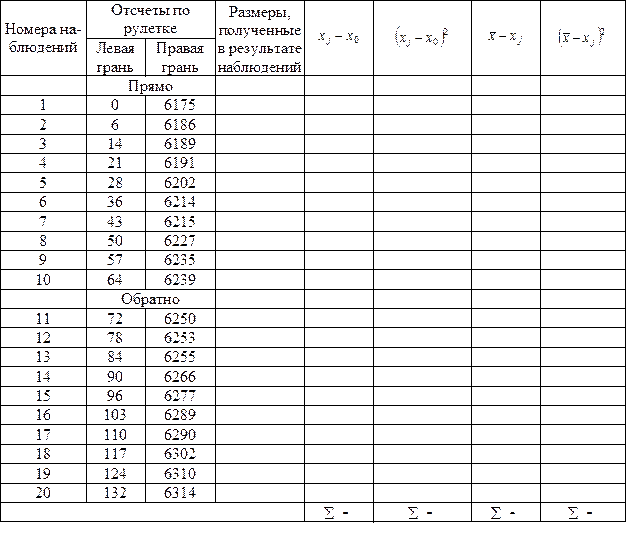Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Грубые погрешности и методы их исключения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практическое занятие №1 ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ.
Грубая погрешность, или промах, – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. При однократных измерениях обнаружить промах невозможно. При многократных измерениях для обнаружения промахов используют статистические критерии, такие как критерий Романовского, критерий Шарлье, критерий Диксона.
Критерий Романовского Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
где Далее расчетное значение bсравнивается с критерием bт, выбранным по табл. 10. Если b³bт, то результат xi считается промахом и отбрасывается.
Таблица № 10 Значения критерия Романовского b = f (n)
Пример решения
При шестикратном измерении расстояний между ориентирами осей здания получены следующие результаты: 25.155; 25,150; 25.165; 25.165; 25.160; 25.180 м. Последний результат вызывает сомнения. Производим проверку по критерию Романовского, не является ли он промахом. Найдем среднее арифметическое значение
Определяем среднее квадратическое отклонение. Для удобства вычислений составим табл. 11.
Таблица № 11 Обработка результатов измерений
Оценка СКО –
Вычисляем b для сомнительного результата
Критическое значение b при уровне значимости 0,05 и n = 6 составляет 2,1. Поскольку 1,58 < 2,1, результат не является промахом и не исключается из результатов измерений.
Критерий Шарлье
Критерий Шарлье используется, если число измерений велико (n > 20). Пользуясь данным критерием, отбрасывается результат, для значения которого выполняется неравенство
Пример решения При измерении расстояний между колоннами были получены следующие результаты (см. табл. 12). Таблица № 12 Обработка результатов измерений
Находим СКО Проверяем сомнительный результат измерения – 23,66. Для этого значения не выполняется неравенство где К ш = 2,13 (см. табл. 13) Таблица № 13 Значения критерия Шарлье
т. е. Таким образом, проверяемое значение 23,66 не является промахом и не отбрасывается. Критерий Диксона
При использовании данного критерия полученные результаты измерений записываются в вариационный возрастающий ряд x1 < x2 < … < xn.. Расчетное значение критерия определяется как
В случае, если расчетное значение критерия будет больше критического значения Zq, то проверяемое значение считается промахом и отбрасывается. Критические значения критерия приведены в табл. 14. Таблица № 14 Значения критерия Диксона
Пример решения
Было произведено шесть измерений расстояний между сваями. Получены следующие результаты: 25,1; 25,2; 24,9; 25,6; 25,1; 25,2 м. Результат 25,6 м существенно отличается от остальных. Произведем проверку, не является ли он промахом. Составим вариационный возрастающий ряд из результатов измерений: 24,9; 25,1; 25,1; 25,2; 25,2; 25,6 м. Для крайнего члена этого ряда 25,6 м расчетный критерий Диксона
Как следует из табл. 14, по этому критерию результат 25,6 м может быть отброшен как промах при уровне значимости q = 0,05.
Задание Определить расстояния между ориентирами осей здания при измерении этого расстояния, заполнить таблицы, определить доверительный интервал, в котором находится это значение, с доверительной вероятностью 0,95 и какие из результатов наблюдений являются промахами. Таблица №1 по критерию Романовского. Таблица №2 по критерию Шарлье и Диксона.
Практическое занятие №2 Пример. Определить систематические погрешности и записать результат с учетом различных параметров. Получен результат измерения длины стальной фермы xi = 24003 мм. Измерение выполнялось 3-метровой рулеткой из нержавеющей стали при t = -20 °С. При этом a1 = 20,5·10-6, a2 = 12,5·10-6, t1 = t2 = -20°С, Решение 1. Поправка на температуру окружающей среды Действительную длину xi фермы с учетом поправки на температуру окружающей среды принимаем равной
2. Поправка на относительную скорость внешней среды
Действительную длину xi фермы с учетом поправки на относительную скорость внешней среды принимаем равной
3. Поправка на длину шкалы средства измерения
Действительную длину xi фермы с учетом поправки на длину шкалы средства измерения принимаем равной
4. Поправка на несовпадение направлений линии измерения и измеряемого размера
Действительную длину xi фермы с учетом поправки несовпадение направлений линии измерения и измеряемого размера принимаем равной
Действительную длину xi фермы с учетом всех поправок принимаем равной
Задание
Определить систематические погрешности и записать результат с учетом различных параметров. Данные результатов измерений приведены в таблице №16
Таблица № 16
Задача 3 А) ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА ВИДА РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
Для предварительной оценки вида распределения по полученным данным строят гистограмму распределений или полигон распределения. В начале производится группирование – разделение данных от наименьшего x min до наибольшего x max на r интервалов. Для количества измерений от 30 до 100 рекомендуемое число интервалов – от 7 до 9. Ширину интервала выбирают постоянной для всего ряда данных, при этом следует иметь в виду, что ширина интервала должна быть больше погрешности округления при записи данных. Ширину интервала вычисляют по формуле
Вычисленное значение h обычно округляют. Например при h = 0,0187 это значение округляют до h = 0,02. Установив границы интервалов, подсчитывают число результатов измерений, попавших в каждый интервал. При построении гистограммы или полигона распределения масштаб этих графиков рекомендуется выбирать так, чтобы высота графика относилась к его основанию примерно как 3 к 5. Пример Построить гистограмму и полигон распределения по полученным экспериментальным данным, приведенным в табл. 17. Таблица № 17 Результаты измерений
Определяем ширину интервала
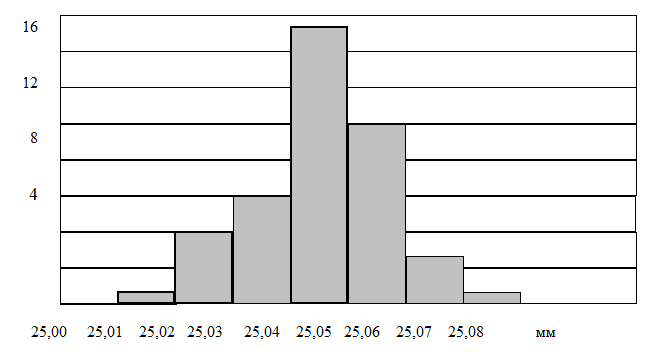
Строим гистограмму распределений (рис. 1), подсчитав число экспериментальных данных, попавших в каждый интервал.
Рис.1. Гистограмма распределений результатов измерений
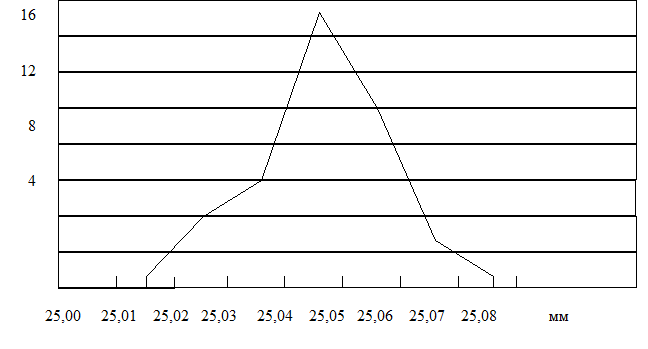
Далее, строим полигон распределения (рис. 2), который представляет собой кусочно-линейную аппроксимацию искомой функции плотности распределения результатов измерения.
Рис. 2. Полигон распределения результатов измерения
Б) ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Нормальный закон распределения, называемый часто распределением Гаусса описывается зависимостью
где σ – параметр рассеивания распределения, равный среднему квадратическому отклонению.
Широкое использование нормального распределения на практике объясняется теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. При количестве измерений n < 10 проверить гипотезу о виде распределения результатов измерения невозможно. При числе данных 10 < n < 50 также трудно судить о виде распределения. Поэтому для проверки соответствия распределения данных нормальному распределению используют составной критерий. Если гипотеза о нормальности отвергается хотя бы по одному из критериев, считают, что распределение результатов измерения отлично от нормального.
Критерий 1. Вычисляют значение d по формуле
где S * – смещенное СКО;
Гипотеза о нормальности подтверждается, если
где
Таблица № 18 Значения процентных точек q для распределения d
Критерий 2. Гипотеза о нормальности распределения результатов измерения подтверждается, если не более m разностей Значения доверительной вероятности P выбирают из табл. 19. Таблица № 19 Значения доверительной вероятности Р
Пример
В табл. 19 приведены результаты измерения угла одним оператором, одним и тем же теодолитом, в одних и тех же условиях. Проверить, можно ли считать, что приведенные в табл. 20 данные принадлежат совокупности, распределенной нормально. Таблица № 20 Результаты исследований
Оценка измеряемой величины равна
Средние квадратические отклонения S и S* найдем по формулам:
Оценка параметра d составит
Уровень значимости критерия 1 примем q = 2%. Из табл. 18 находим d 1% = = 0,92 и d 99% = 0,68. При определении d 1% и d 99% использовалась линейная интерполяция ввиду того, что значение n = 14 в таблице отсутствует. Критерий 1 выполняется, так как Применим критерий 2. Выбрав уровень значимости q = 0,05 для n =14 из табл. 11, найдем Р = 0,97. Из табл. 21 определим zp/2 = 2,17. Тогда
S ∙ zp/2 = 3,245 ∙ 2,17 = 7,042.
Таблица № 21 Значения Р- процентных точек нормированной функции Лапласа
Согласно критерию 2, не более одной разности Следовательно, гипотеза о нормальности распределения данных подтверждается. Уровень значимости составного критерия: q £ 0,02 + 0,05 = 0,07, т. е. гипотеза о нормальности распределения результатов измерения подтверждается при уровне значимости не более 0,07.
Задание
Произвести проверку нормальности распределения измерений по данным приведенным в таблице № 22 и по полученным данным построить гистограмму распределений или полигон распределения. Таблице № 22
Задача 4 Пример Произвести обработку результатов измерений, данные которых представлены в табл. 24.
Таблица № 24 Результаты измерений
1.Определение точечных оценок закона распределения результатов измерений
Определяем среднее арифметическое значение результатов измерений
Среднее квадратическое отклонение результатов измерения
Производим проверку на наличие грубых погрешностей в результатах измерения по критерию Диксона. Составим вариационный возрастающий ряд из результатов измерений: 36,007; 36,008; 36,009; 36,010; 36,011; 36,012. Найдем расчетное значение критерия для значения 36,012
Как следует из таблицы 5, по этому критерию результат 36,012 не является промахом при всех уровнях значимости.
2. Предварительная оценка вида распределения результатов измерений или случайных погрешностей При числе измерений меньше 15 предварительная оценка вида распределения результатов наблюдений не производится
3.Оценка закона распределения по статистическим критериям При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
4.Определение доверительных границ случайной погрешности При числе измерений n= 11 используем распределение Стьюдента, при этом доверительные границы случайной погрешности Коэффициент Стьюдента при доверительной вероятности Рд = 0,95 и при n = 11 равен 2,23. Тогда доверительные границы случайной погрешности
5.Определение границ неисключенной систематической погрешности результата измерения Границы неисключенной систематической погрешности q принимаются равными пределам допускаемых основных и дополнительных погрешностей средства измерения. Для рычажного микрометра допускаемая погрешность равна ± 0,7 мкм.
6. Определение доверительных границ погрешности результата измерения
Согласно ГОСТ 8.207–76 погрешность результата измерения определяется по следующему правилу. Если границы неисключенной систематической погрешности q < 0,8 Sx, то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. В нашем случае q = 1,4 мкм, а Sx = 2 мкм, т.е. соотношение q < 0.8 Sx выполняется, поэтому систематической погрешностью пренебрегаем.
7. Запись результата измерения
Результат измерения –
Задание Используя данные в таблице №25 произвести обработку результатов прямых многократных измерений
Таблица № 25
Практическое занятие №5 Пример. Определить момент инерции круглой платформы, связанный формулой
со следующими величинами, измеряемыми прямыми способами: R = (11,50 ± 0,05) 102м — радиус платформы; r = (10,00 ± 0,05) 102 м — радиус верхнего диска подвеса; l = (233,0 ± 0,2) 102 м — длина нитей подвеса; m = (125,7 ±0,1) 103 кг — масса платформы; T = (2,81 ± 0,01) с — период малых колебаний платформы; g = 9,81 м с г — ускорение свободного падения; π = 3,14. Результаты приведены со средними квадратичными отклонениями. Решение. Подставляя в исходную формулу средние арифметические значения измеряемых прямыми способами величин и округленные значения постоянных, получим оценку истинного значения моментов инерции платформы.
так как результат должен быть округлен до трех значащих цифр. Для оценки точности полученного результата вычислим частные производные и частные погрешности косвенных измерений:
Таким образом, среднее квадратичное отклонение косвенного измерения момента инерции платформы составит
Окончательно результат косвенного измерения записывается в виде I =(1,22 ±·0,01) 10 3 кг м2.
Задание
Определить предельное усилие при растяжении полос при сварке в стык по длинной полосе, по данным приведенным в таблице № 26
Таблица № 26
Продолжение таблица № 26
Практическое занятие №6 Пример Определить в каком интервале находится измеренное значение, если при выполнении измерения прибором, имеющим на щитке обозначение
Решение Определяем абсолютную погрешность измерения И измеряемое значение будет находиться в интервале 200±1 Задание
Практическое занятие №7 ВЫБОР СРЕДСТВ ИЗМЕРЕНИЙ.
Расчет погрешности при выборе методов и средств измерения выполняют в соответствии с требованиями ГОСТ 26433.0-85. Методы и средства измерений принимаем в соответствии с характером объекта и измеряемых параметров из условия. где
Вычисляем расчетную погрешность измерения по одной из формул: или где При расчете по указанным формулам принимаем, что составляющие погрешности независимы между собой или слабо коррелированны.
Предельную погрешность где К - коэффициент, зависящий от цели измерений и характера объекта. Для измерений, выполняемых в процессе и при контроле точности изготовления и установки элементов, а также при контроле точности разбивочных работ принимаем К = 0,2. Для измерений, выполняемых в процессе производства разбивочных работ, К = 0,4. Действительная погрешность Для случаев, когда процесс измерения состоит из большого числа отдельных операций, на основе принципа равных влияний определяем среднее значение составляющих погрешностей где Выделяем те составляющие погрешности, которые легко могут быть уменьшены, увеличивая соответственно значения тех составляющих погрешностей, которые трудно обеспечить имеющимися методами и средствами. Проверяем соблюдение условия (1) и в случае несоблюдения этого условия назначают более точные средства или принимают другой метод измерения.
Пример Выбрать средство измерения для контроля длины изделия, L = 3600 ± 2,0 мм (
Решение 1. Определяем предельную погрешность измерения 2. Для выполнения измерений применяем, например, 10-метровую металлическую рулетку 3-го класса точности ЗПК3-10АУТ/10 ГОСТ 7502-80. 3. В суммарную погрешность измерения длины изделия рулеткой входят составляющие погрешности: Определяем значения этих погрешностей. 3.1. Погрешность 3.2. Погрешность 3.3. Погрешность
где F = 2 мм2 - площадь поперечного сечения рулетки; E = 2·105Н/мм - модуль упругости материала рулетки. 3.4. Экспериментально установлено, что погрешность снятия отсчета по шкале рулетки не превышает 0,3 мм, при этом погрешность 4. Определяем расчетную суммарную погрешность измерения по формуле (2), учитывая, что 5. Данные метод и средство измерения могут быть приняты для выполнения измерений, так как расчетная суммарная погрешность измерения
Задание
По выше описанному алгоритму произвести выбор средства измерения с учетом погрешности, используя данные в таблице №6
Таблица № 6
Практическое занятие №8 Пример. Произвести предварительную оценку точности измерений рулеткой длины изделий при контроле точности их изготовления. Решение Измерение длины каждого изделия в процессе контроля будут выполняться при числе наблюдений m = 2. Выполняем многократные наблюдения длины одного изделия при числе наблюдений М = 10. Для уменьшения влияния систематической погрешности первые пять наблюдений выполняем в одном направлении каждый раз со сдвигом шкалы рулетки на 70 - 90 мм, а вторые пять наблюдений - в другом направлении с тем же сдвигом шкалы. Результаты наблюдений и последовательность их обработки приведены в табл. 8 (приведены результаты 10 наблюдений, т.е. М = 10). Таблица № 8
1. Определяем среднее арифметическое из результатов измерений:
Принимаем 2. Контроль правильности вычислений: а). б). 3. Среднее квадратическое отклонение результата измерений находим по формуле 4. Действительная погрешность измерения будет составлять. 5. Предельную погрешность измерения находим по формуле При допуске на длину 16.5 мм по 16 квалитету 6. Проверяем соблюдение условия 5,0 > 3,3 мм. Действительная погрешность измерения не соответствует требуемой, должны быть приняты другие средства измерений или увеличено количество наблюдений т. Принимаем т = 5, тогда 3.2мм < 3,3 мм.
Задание
По выше описанному алгоритму произвести оценку точности произведенных измерений, заполнить таблицу, используя данные в таблице №9
Таблица № 9
Практическое занятие №1 ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ.
Грубая погрешность, или промах, – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. При однократных измерениях обнаружить промах невозможно. При многократных измерениях для обнаружения промахов используют статистические критерии, такие как критерий Романовского, критерий Шарлье, критерий Диксона.
Критерий Романовского Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
где Далее расчетное значение bсравнивается с критерием bт, выбранным по табл. 10. Если b³bт, то результат xi считается промахом и отбрасывается.
Таблица № 10 Значения критерия Романовского b = f (n)
Пример решения
При шестикратном измерении расстояний между ориентирами осей здания получены следующие результаты: 25.155; 25,150; 25.165; 25.165; 25.160; 25.180 м. Последний результат вызывает сомнения. Производим проверку по критерию Романовского, не является ли он промахом. Найдем среднее арифметическое значение
Определяем среднее квадратическое отклонение. Для удобства вычислений составим табл. 11.
Таблица № 11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 11628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.209 (0.011 с.) |

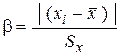 ,
,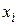 – проверяемое значение,
– проверяемое значение, 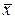 – среднее арифметическое значение измеряемой величины, Sx – среднее квадратическое отклонение.
– среднее арифметическое значение измеряемой величины, Sx – среднее квадратическое отклонение.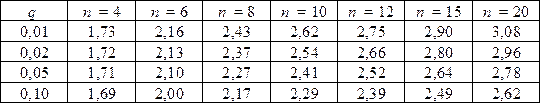
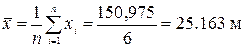
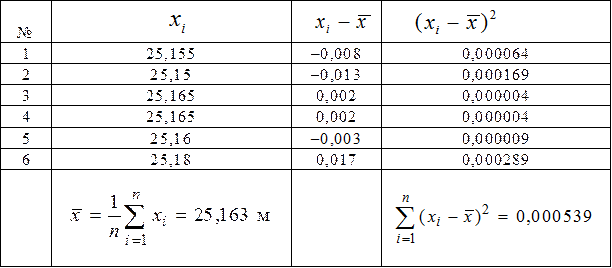
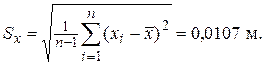
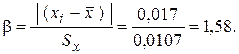
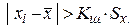

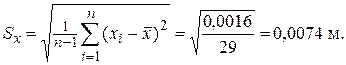
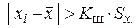 ,
,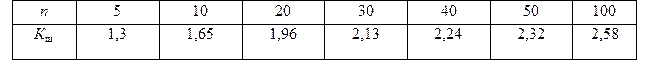
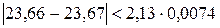
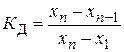 .
.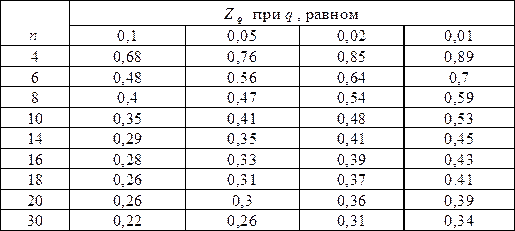
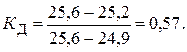
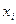 ), м
), м
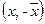 , мм
, мм
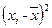 мм2
мм2
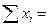
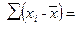
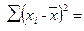
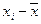 , мм
, мм
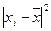 , мм2
, мм2
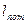 = 3000 мм,
= 3000 мм, 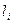 = 3002 мм, h = 35 мм, P = 9 Н, Q = 1,2 Н.
= 3002 мм, h = 35 мм, P = 9 Н, Q = 1,2 Н.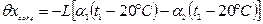 мм.
мм. = -24003[20,5·10-6(-20 - 20) - 12,5·10-6(-20 - 20)]» 7,7 мм.
= -24003[20,5·10-6(-20 - 20) - 12,5·10-6(-20 - 20)]» 7,7 мм.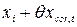 = 24003 + 7,7 = 24010,7 мм.
= 24003 + 7,7 = 24010,7 мм.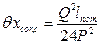 мм.
мм. мм.
мм.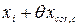 = 24003 + 2,22 = 24002,22 мм.
= 24003 + 2,22 = 24002,22 мм.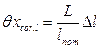 мм.
мм.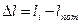 мм.
мм.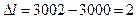 мм.
мм.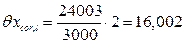 мм.
мм.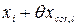 = 24003 + 16,002 = 24019,002 мм.
= 24003 + 16,002 = 24019,002 мм.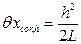 мм.
мм.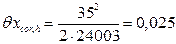 мм.
мм.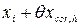 = 24003 + 0,025 = 24003,025 мм.
= 24003 + 0,025 = 24003,025 мм.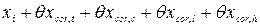 = 24003 + 7,7 + 2,22 + 16,002 + 0,025 = 24028,9 мм.
= 24003 + 7,7 + 2,22 + 16,002 + 0,025 = 24028,9 мм.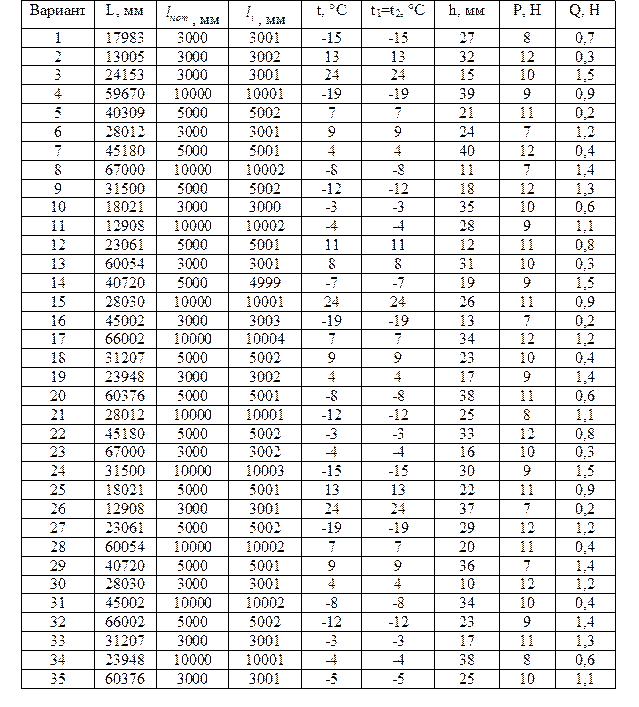
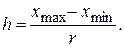
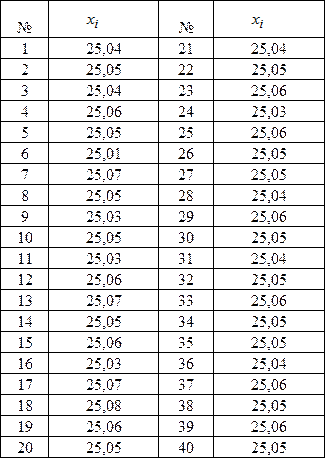

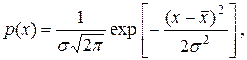
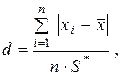
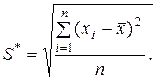
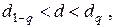
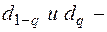 процентные точки распределения значений d, которые находятся по табл. 18.
процентные точки распределения значений d, которые находятся по табл. 18.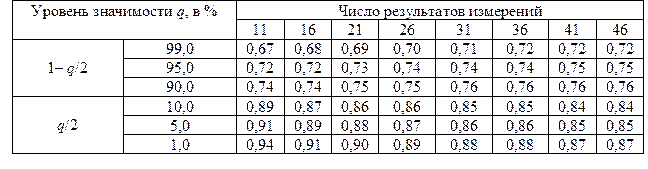
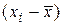 превзошли значения S×zp/2. Здесь
превзошли значения S×zp/2. Здесь 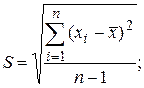 zp/2 – верхняя 100 ∙ P/2 – процентная точка нормированной функции Лапласа
zp/2 – верхняя 100 ∙ P/2 – процентная точка нормированной функции Лапласа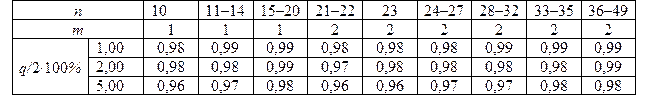
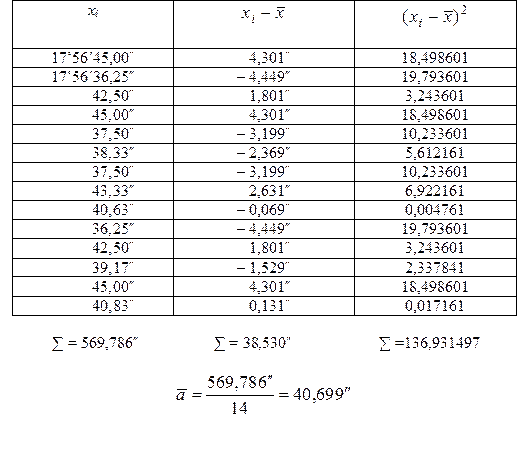
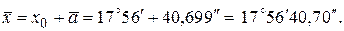
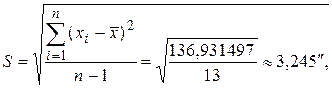
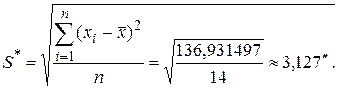
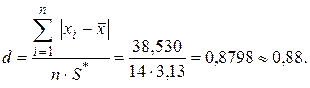
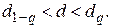 В нашем случае это – 0,68 < 0,88 < 0,92.
В нашем случае это – 0,68 < 0,88 < 0,92.
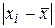 может превзойти 7,042. Из данных табл. 20 следует, что ни одно отклонение
может превзойти 7,042. Из данных табл. 20 следует, что ни одно отклонение 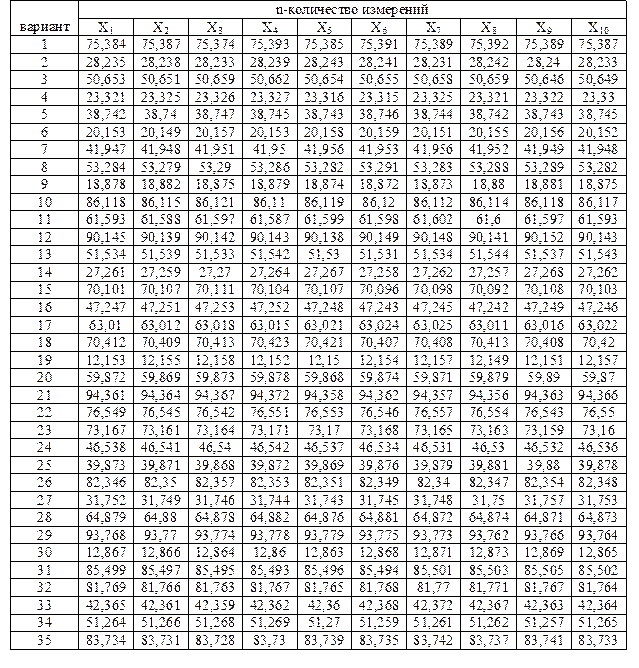
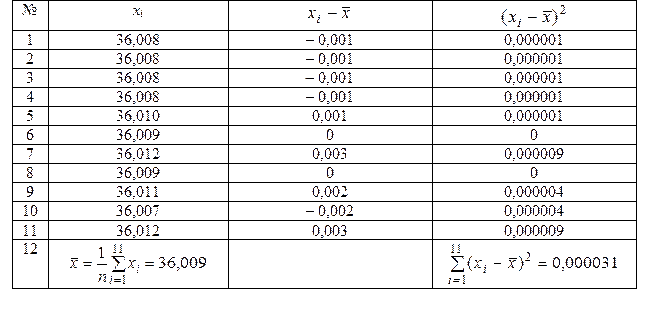
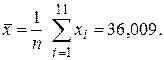
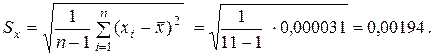
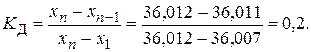
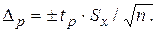
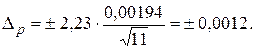
 при доверительной вероятности Р = 0,95.
при доверительной вероятности Р = 0,95.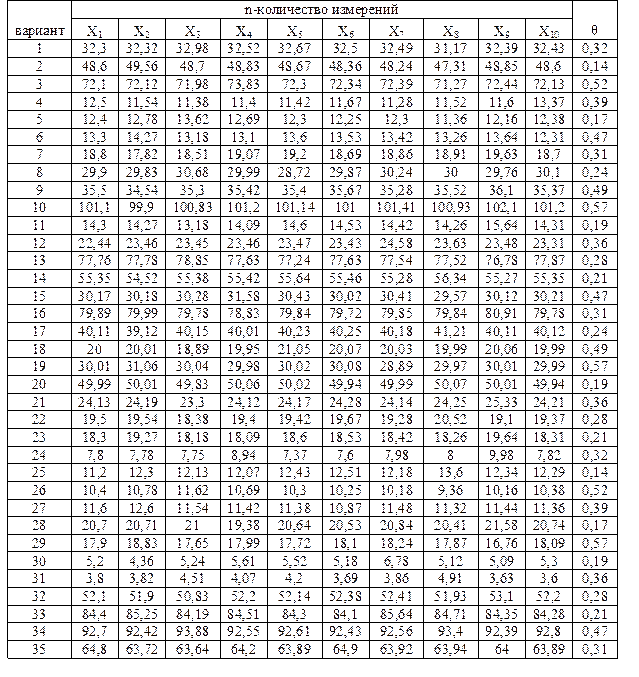
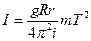 ,
,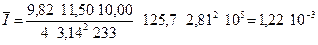 кг м2,
кг м2,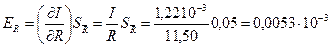 кг м2
кг м2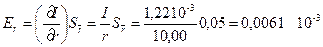 кг м2
кг м2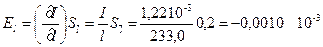 кг м2
кг м2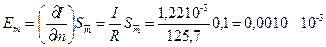 кг м2
кг м2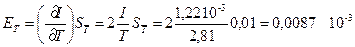 кг м2
кг м2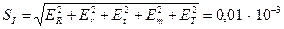 кг м2.
кг м2.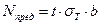
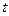 - толщина полосы
- толщина полосы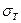 - предел текучести
- предел текучести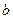 - ширина полосы
- ширина полосы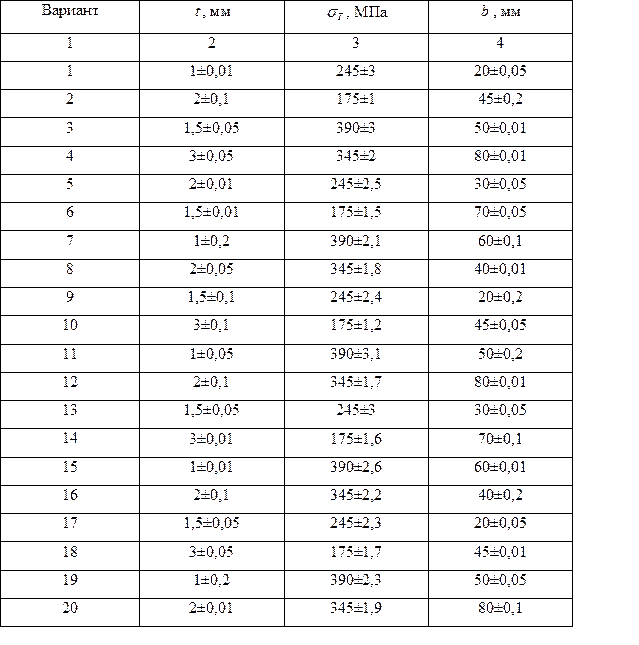
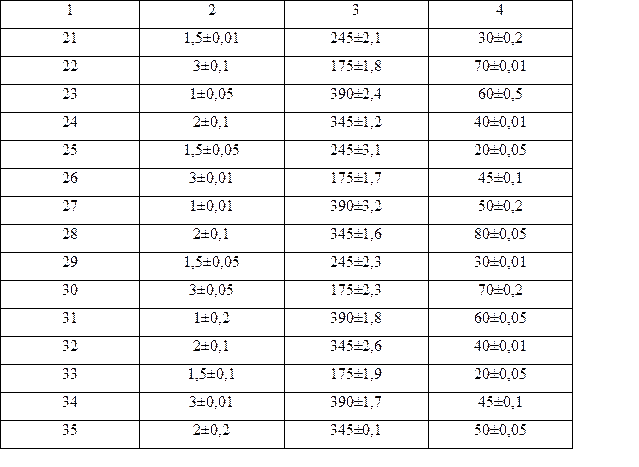
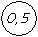 , и полученный результат равен 200.
, и полученный результат равен 200.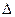
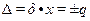
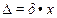 = 0,005·200 = ±1
= 0,005·200 = ±1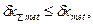 (1)
(1)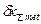 - расчетная суммарная погрешность принимаемого метода и средства измерения;
- расчетная суммарная погрешность принимаемого метода и средства измерения;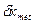 - предельная погрешность измерения.
- предельная погрешность измерения.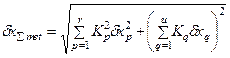 (2)
(2)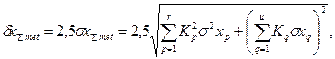 (3)
(3)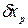 - случайные составляющие погрешности;
- случайные составляющие погрешности;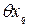 - систематические составляющие погрешности;
- систематические составляющие погрешности;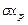 - средние квадратические случайные составляющие погрешности;
- средние квадратические случайные составляющие погрешности;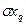 - средние квадратические систематические составляющие погрешности;
- средние квадратические систематические составляющие погрешности;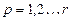 - число случайных составляющих погрешностей;
- число случайных составляющих погрешностей;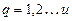 - число систематических составляющих погрешностей;
- число систематических составляющих погрешностей;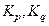 - коэффициенты, учитывающие характер зависимости между суммарной и каждой из составляющих погрешностей измерения.
- коэффициенты, учитывающие характер зависимости между суммарной и каждой из составляющих погрешностей измерения.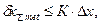 (4)
(4)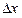 - допуск измеряемого геометрического параметра, установленный нормативно-технической документацией на объект измерения;
- допуск измеряемого геометрического параметра, установленный нормативно-технической документацией на объект измерения;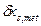 выполненных измерений не должна превышать ее предельного значения.
выполненных измерений не должна превышать ее предельного значения.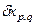 по формуле
по формуле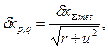 (5)
(5)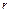 - число случайных составляющих погрешностей;
- число случайных составляющих погрешностей;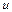 - число систематических составляющих погрешностей.
- число систематических составляющих погрешностей.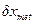
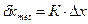 мм
мм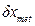 = 0,2·4,0 = 0,8 мм
= 0,2·4,0 = 0,8 мм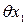 - поверки рулетки;
- поверки рулетки; 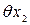 - от погрешности измерения температуры окружающей среды;
- от погрешности измерения температуры окружающей среды; 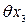 - от колебания силы натяжения рулетки;
- от колебания силы натяжения рулетки; 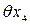 - снятия отсчетов по шкале рулетки на левом и правом краях изделия.
- снятия отсчетов по шкале рулетки на левом и правом краях изделия.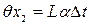 мм.
мм.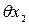 = 3600·12,5·10-6·0,5» 0,22 мм.
= 3600·12,5·10-6·0,5» 0,22 мм.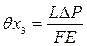 мм,
мм,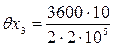 = 0,09» 0,1 мм,
= 0,09» 0,1 мм,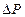 = 10Н - погрешность натяжения рулетки вручную;
= 10Н - погрешность натяжения рулетки вручную;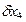 снятия отсчетов на левом и правом краях изделия составит
снятия отсчетов на левом и правом краях изделия составит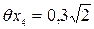 мм.
мм.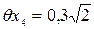 »0,4 мм.
»0,4 мм.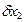 ,
, 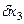 и
и 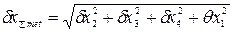 мм.
мм.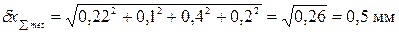
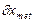 = 0,8 мм, что соответствует требованию.
= 0,8 мм, что соответствует требованию.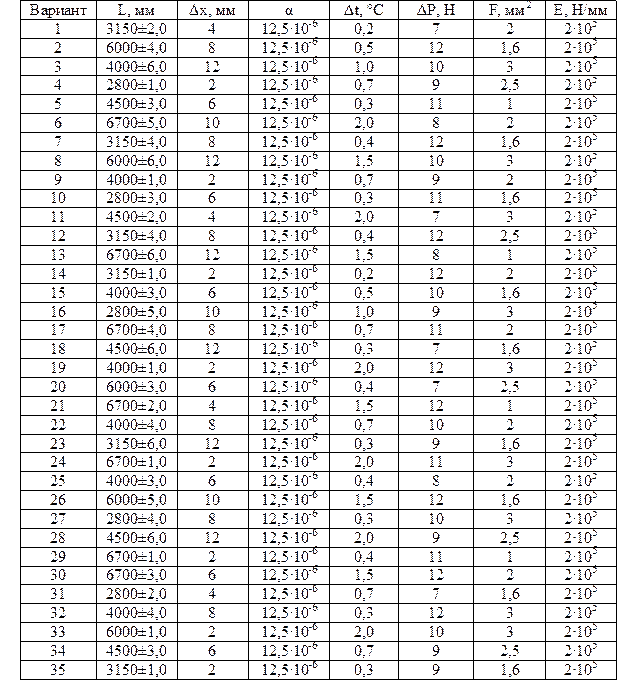
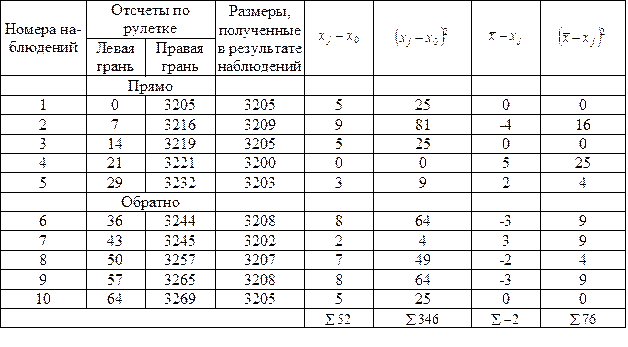
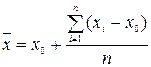 , мм.
, мм.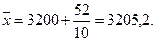 мм.
мм.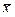 = 3205,0 мм. с ошибкой округления а = -0,2 мм.; х0 - наименьший результат из всех наблюдений, х0 =3200 мм..
= 3205,0 мм. с ошибкой округления а = -0,2 мм.; х0 - наименьший результат из всех наблюдений, х0 =3200 мм..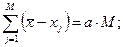
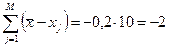 мм.
мм.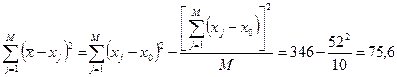 мм.
мм.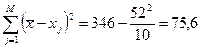 мм.
мм.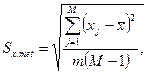 мм.
мм.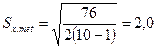 мм.
мм.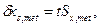 мм.
мм. мм.
мм.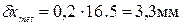
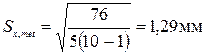
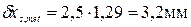 .
.