
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка и правила округления погрешностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оценки погрешностей могут быть точечные и интервальные. Точечные оценки определяются одним значением. Например, для систематической погрешности такой оценкой может быть предел ее абсолютной величины (предел сверху). Интервальные оценки обозначают границы погрешностей сверху и снизу (например, плюсовой и минусовой допуски к размерам изделий). Вероятностные оценки (доверительные интервалы) обозначают границы, в пределах которых находится истинное значение измеряемой величины с заданной вероятностью. Предельные (безусловные) оценки соответствуют вероятности, равной P = 1.
Принципы оценки погрешностей 1. Как отмечалось выше, погрешность результата измерений складывается из различных составляющих. Поэтому оценивать погрешность можно или по каждой составляющей, или в целом. Последний способ часто оправдан, поскольку каждую составляющую погрешности учесть сложно. 2. Оценки погрешности берутся приближенными с достаточной точностью (нет необходимости мерить точнее, чем рассчитывать, равно, как и наоборот). 3. Погрешность оценивается, как правило, сверху («в запас»).
Правила округления погрешностей 1.Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной - если первая цифра равна 3 или более. Пример. Погрешность 1,2%, 2,3%, но 3%, 5%. 2.Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности. Пример. Погрешность измерений длины определяется с точностью до 0,1 мм. Результаты измерений записываются в следующем виде: 23,4 мм, 13,0 мм. 3.Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если цифра старшего из отбрасываемых разрядов больше 5 или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу. Пример. Точность измерений длины – 10 см. Результаты измерений округляются следующим образом: 364 см – 360 см, 366 см – 370 см, 36 м – 36,0 м, 36,12 м – 36,1 м, 36,15 м – 36,2 м. 4.Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Пример. Точность измерений длины – 10см. В этом случае 365см записывается как 360см, 375 см – 380см. 5.Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним - двумя лишними знаками. Пример. Точность измерений длины моста – 0,5м. Схема пролетов: 11,2+15,7+11,2 м. Неправильно: 11,0+15,5+11,0 = 37,5м; Правильно: 11,2+15,7+11,2 = 38,1м ≈ 38,0м. Суммирование погрешностей В общем случае погрешность измерений образуется по совокупности причин и представляет собой результат суммирования нескольких ее составляющих. Правила суммирования погрешностей, составляющих результирующую погрешность, должны учитывать характер каждой из них и вероятность их сочетания. Практические правила суммирования состоят из следующих расчетных процедур. 1) Все суммируемые погрешности, так же как и результирующая, представляются как случайные величины. Суммирование заключается в определении параметров распределения результирующей погрешности. 2) Все суммируемые составляющие необходимо разделить на аддитивные и мультипликативные. 3) Для каждой составляющей погрешности следует вычислить параметры ее распределения: среднее значение и стандарт. Для мультипликативных погрешностей эти параметры определяются в начале и конце диапазона измерений. 4) Необходимо учесть корреляционные связи между составляющими погрешностями и по определенным критериям, выделить группы сильно коррелированных между собой погрешностей, для которых принять коэффициент корреляции – 1, а также группы слабо коррелированных погрешностей, в которых корреляцию не учитывать. 5) Для определения суммарной погрешности и параметров ее распределения при наличии мультипликативных погрешностей эти параметры вычисляют для начального и конечного значений измеряемой величины, а их промежуточные значения определяют по интерполяции. 6) Параметры распределения результирующей погрешности Z определяются по правилам суммирования случайных величин на начало и конец измерений по следующим формулам. Средняя величина (алгебраическая сумма):
.. (2.3)
Стандарт для слабо коррелированных между собой погрешностей:
где m – число суммируемых погрешностей.
Контрольные вопросы: 1. Дайте определение погрешности измерений. 2. Объясните различия погрешности по характеру их проявления. 3. Назовите возможные причины погрешностей измерения. 4. Назовите правила округления погрешностей. Приведите примеры. 5. Как суммируются сильно и слабо коррелированные составляющие погрешности? Систематические погрешности Систематическая погрешность представляет собой функцию влияния на результаты измерений определенных факторов, состав которых зависит от физических, конструктивных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Пример. При измерении профиля проезжей части моста могут возникнуть систематические погрешности вследствие негоризонтальности трубы нивелира, неучета влияния солнечной радиации и т.п.
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.45 (0.006 с.) |

 . (2.2)
. (2.2)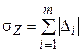 Стандарт для сильно коррелированных между собой погрешностей:
Стандарт для сильно коррелированных между собой погрешностей: , (2.4)
, (2.4)


