
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила работы в лабораторииСодержание книги
Поиск на нашем сайте
ПРАКТИКУМ ПО МЕХАНИКЕ И МОЛЕКУЛЯРНОЙ ФИЗИКЕ
Учебное пособие для вузов
Издательско-полиграфический центр Воронежского государственного университета
Утверждено Научно-методическими советами биолого-почвенного (протокол № 6 от 21.02.2008 г.), геологического (протокол №4 от 21.02.2008 г.) и химического (протокол № 4 от 06.03.2008г г.) факультетов
Составители: А.С. Сидоркин, С.Д. Миловидова, О.В. Рогазинская, А.П. Лазарев, Л.П.Нестеренко, А.М.Косцов
Учебное пособие подготовлено на кафедре экспериментальной физики физического факультета Воронежского государственного университета.
Рекомендуется в качестве учебного пособия к лабораторным работам для студентов 1 и 2 курсов биолого-почвенного, геологического и химическиого факультетов.
Работа выполнена при поддержке гранта VZ-010 Американского фонда гражданских исследований и развития (CRDF) и по программе «Фундаментальные исследования и высшее образование»
Для специальностей: 020101 (011000) – Химия 020301 (011100) – Геология 020306 (013300) – Экологическая геология 020304 (014400) – Гидрогеология и инженерная геология 020302 (011200) – Геофизика 020201 (011600) – Биология 020701 (013000) – Почвоведение СОДЕРЖАНИЕ 1.1. Правила работы в лаборатории. Оформление результатов работы……..4 1.2. Обработка результатов физического эксперимента…………...................5 1.3. Изучение измерительных приборов……………………………………...11 1.4. Определение плотности твердых тел, имеющих правильную геометрическую форму…………………………………………………...15 2. Гармонические колебания ….………………………………………….…..17 2-1. Исследование законов колебательного движения математического и оборотного маятника на установке с электронным секундомером....…..21 2-2. Проверка законов колебания математического маятника и определение ускорения свободного падения …………. …...………....24 3. Затухающие колебания ……………………………………………….…… 26 3-1. Определение логарифмического декремента затухания и коэффициента затухания крутильных колебаний ………………….…29 3-2. Определение логарифмического декремента затухания и коэффициента затуханий колебаний математического маятника ……30 4. Изучение законов динамики поступательного движения с помощью машины Атвуда …………………………………………..…32 5. Вращательное движение твердых тел…………………………………….35 5-1. Определение моментов инерции твердых тел при помощи крутильных колебаний ……………………………………………………38 5-2. Определение моментов инерции твердых тел с помощью маятника Максвелла ………………………………………………………41 5-3. Определение моментов инерции твердых тел с помощью трифилярного подвеса …………………………………………..……….. 44 5-4. Исследование вращательного движения твердых тел с помощью маятника Обербека …………………...…………………………………...46 6. Определение скорости полета «пули» с помощью баллистического маятника ………………………………….…………....49 7. Исследование закона сохранения импульса при центральном ударе шаров……………………………………………….……………….……....52 8. Определение коэффициента внутреннего трения и средней длины свободного пробега молекул воздуха……………………………………...56 9. Определение модуля Юнга методом прогиба………………………….…58 10. Определение модуля сдвига из крутильных колебаний……….………..62 11. Определение коэффициента вязкости жидкости по методу Стокса……66 12. Определение отношения удельных теплоемкостей газов методом Клемана-Дезорма…………………………………………………………..71 13. Определение скорости звука в воздухе и отношение удельных теплоемкостей ср/сv для воздуха методом стоячихзвуковых волн……...76 14. Определение коэффициента поверхностного натяжения жидкости методом компенсации дополнительного давления ……………………..81 1.1. ПРАВИЛА РАБОТЫ В ЛАБОРАТОРИИ, Перед началом выполнения лабораторного практикума каждый студент обязан пройти инструктаж по технике безопасности!!! Правила работы в лаборатории В начале семестра составляется график выполнения работ на весь семестр. Студент должен заранее знать тему своей лабораторной работы и подготовиться к ней по методическому руководству и другой указанной в нем литературе. Перед выполнением каждой лабораторной работы необходимо пройти краткое собеседование с преподавателем и получить разрешение на ее выполнение. Оно дается в том случае, если студент четко знает цель работы, методику проведения эксперимента, умеет пользоваться приборами. При выполнении лабораторной работы используются только те приборы и принадлежности, которые указаны в методическом руководстве к ней. Приступать к выполнению лабораторных работ без разрешения преподавателя категорически воспрещается! В конце занятия студент обязан предъявить преподавателю результаты своей работы. Работа считается выполненной, если результаты утверждены и подписаны преподавателем. После этого необходимо выключить установку, привести в порядок рабочее место. И обязательно узнать, какую работу студент будет выполнять на следующем занятии. Оформление отчетов По результатам каждой лабораторной работы составляется отчет. Он должен включать: 1. Краткую теорию, описание метода исследования, все необходимые формулы, в том числе и расчетную с пояснением физического смысла входящих в нее символов (0,5-1 стр.). 2. Условия опыта – температуру, давление и т.д. (если это важно). 3. Далее следует раздел «Выполнение работы» с обязательным названием каждого упражнения. 4. Таблицы с результатами измерений и расчетов. Таблицы составляются так, чтобы из них было ясно, какие физические величины и в каких единицах измерялись, сколько раз повторялись измерения каждой физической величины. 5. Статистическую обработку результатов измерений. 6. Выводы. Они должны быть аргументированы ссылками на соответствующие таблицы и графики, которые должны быть пронумерованы. Отчет должен быть написан в хорошем стиле, аккуратным разборчивым почерком. При его оформлении не следует также пренебрегать и эстетической стороной вопроса. Заголовки, выводы и формулы целесообразно выделять пастой другого цвета, подчеркнуть и т.п. Это облегчает чтение отчета. Графики Графики используются для наглядного представления результатов. При их построении необходимо соблюдать ряд правил: 1. Графики нужно строить только на миллиметровой бумаге. 2. На осях необходимо нанести масштабную сетку, указать единицы измерения и символы изображаемых величин. 3. Масштаб должен быть простым, удобным для отсчета его долей. Например, 1 см = 0,1; 1; 2 или 10 единиц. Кроме того, масштаб выбирают так, чтобы все экспериментальные точки вошли в график и достаточно далеко отстояли друг от друга. Иногда для этой цели бывает удобно сместить начало отсчета вдоль осей. Масштаб по осям Х и У может быть различен.
4. График должен представлять собой плавную кривую без изломов и перегибов. Нужно стремиться провести кривую так, чтобы экспериментальные точки равномерно распределялись по обе стороны от нее (рис. 1).Графики, выполненные на миллиметровой бумаге, аккуратно вклеиваются в отчет, где для них необходимо предусмотреть соответствующее место. Т.е., если приходится измерять различные величины и пределы возможной точности у них оказываются различными, то нет оснований при отдельных измерениях выходить за пределы точности наименее точно измеряемой величины. По характеру влияния на результаты измерений погрешности делятся на 3 типа: систематические, случайные, промахи. Систематическими называются погрешности, величина которых не меняется при повторении измерений данной величины в тех же условиях (тем же методом, теми же приборами и т. д.).Систематические погрешности возникают в тех случаях, когда не учитывается влияние на результаты эксперимента различных постоянно действующих факторов: температуры, давления, влажности воздуха, выталкивающей силы Архимеда, сопротивления подводящих проводов, контактных ЭДС и т. п. Источниками систематических погрешностей могут быть также измерительные приборы вследствие неточности их градуировки или неисправности. Исключение систематических погрешностей требует принятия специальных мер предосторожности. К ним относятся: 1. Своевременный ремонт и систематическая проверка приборов. 2. Использование специальных способов измерения (например, двойное взвешивание для исключения неравноплечности весов, использование охранных колец при измерении объемного сопротивления плохих проводников, позволяющее исключить влияние их поверхности) 3. Внесение соответствующих поправок на влияние внешних факторов. Промах – это очень грубая погрешность, вызванная невнимательностью экспериментатора (неверный отсчет показаний прибора, описка при записи показаний и т. д.). Промахи могут сильно исказить результаты измерений, особенно в тех случаях, когда их число невелико. Вывод: при выполнении работы нужно быть очень внимательным, не спешить, не отвлекаться. Случайными называются погрешности, величина и знак которых меняется непредсказуемым образом при повторных измерениях данной величины в тех же условиях. Случайные погрешности могут быть вызваны неточностью отсчетов, которую непроизвольно вносит в измерение экспериментатор, и которые являются следствием несовершенства наших органов чувств и некоторых других обстоятельств, которые не могут быть заранее учтены (изменения давления воздуха, температуры, толчки здания, влияющие на показания точного зеркального гальванометра и т. д.). Многократное повторение отсчетов измерения снижает уровень случайных ошибок. Среднее арифметическое из большого числа измерений, конечно, ближе всего к истинному значению измеряемой величины. Вот почему в лабораторной практике всегда проводят неоднократное измерение какой-либо величины. Случайные погрешности подчиняются законам теории вероятности. В дальнейшем мы будем говорить только о случайных погрешностях, опуская слово «случайные». В основе теории погрешностей лежат три аксиомы: 1. Случайные погрешности, равные по абсолютной величине, но противоположные по знаку, равновероятны. Это означает, что мы можем с одинаковой вероятностью ошибаться как в одну, так и в другую сторону (как в меньшую, так и в большую). 2. Среднее арифметическое из случайных погрешностей измерений одной и той же величины при увеличении числа измерений стремится к нулю. 3. Чем больше по абсолютной величине погрешность измерения, тем меньше ее вероятность, т.е. тем реже она встречается. Теперь выясним, как вычисляются погрешности при прямых измерениях, а затем при косвенных. Нониусы Часто при измерении длины какого-либо тела длина его не укладывается в целое число делений масштаба. Для того чтобы можно было поручиться при линейных измерениях и за десятые доли масштаба (а иногда и за сотые), пользуются нониусом. Нониус – это дополнительная шкала к основному масштабу (линейному или круговому), позволяющая повысит точность измерения с данным масштабом в 10, 20 и более число раз.
Линейный нониус представляет собой небольшую линейку (шкалу), скользящую вдоль большей масштабной линейки (рис.2). Как видно из рис.1, 10 делений нониуса соответствуют 9 делениям основного масштаба. В случае прямого нерастянутого нониуса, который мы рассматриваем, одно деление нониуса короче одного деления масштаба на величину Δ, которая называется точностью нониуса. Точность нониуса Δ является разностью длин делений основного масштаба и нониуса и легко может быть определена, если мы знаем число делений нониуса n и длину наименьшего деления масштаба αm
Погрешность, которая может возникнуть при таком методе отсчета, будет обуславливаться неточным совпадение деления нониуса с одним из делений масштаба, и величина ее не будет превышать, очевидно, Чтобы легче было заметить, какое деление нониуса совпадает с каким- либо делением основной шкалы, на практике делают нониусы растянутыми. Прямой растянутый нониус получится, если длина одного деления нониуса будет короче не одного наименьшего деления масштаба (как мы полагали до сих пор), а двух, трех и т.д. наименьших делений его. Точность нониуса в этом случае определяется по той же формуле.
Очень часто в круговых нониусах αм=0,5о=30 минут, а n равно 15 или 30, в таком случае точность нониуса, соответственно равна двум минутам или одной минуте. В лабораторной практике для измерения длин, площадей и объемов наиболее распространенными приборами являются штангенциркуль и микрометр.
Штангенциркуль (рис.5) служит для линейных измерений, не требующих высокой точности. Отсчетным приспособлением у всех конструкций штангенциркулей служит основная масштабная шкала штанги 1, цена деления которой 1 мм, и линейный нониус на подвижной рамке 2. Он представляет собой небольшую линейку, скользящую вдоль основного масштаба. На этой линейке нанесена маленькая шкала, состоящая из m делений. При нулевом показании инструмента нуль нониуса совпадает с нулевым штрихом основной шкалы. При измерении подвижная рамка с нониусом смещается и предмет зажимается губками 3 штангенциркуля. Так как цена деления нониуса не равна цене деления масштаба, то обязательно найдется на нем такое деление, которое будет ближе всего подходить к какому-то делению масштаба. Правило отсчета можно сформулировать следующим образом: длина предмета, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. В лабораторной практике обычно используются штангенциркули с точностью 0,1 и 0,05 мм, которая указывается на приборе. Для измерения внутренних размеров тел служат обычно верхние заостренные ножки 4. Если же штангенциркуль не имеет верхних ножек, то измерение внутренних размеров производится теми же ножками, которые служат для обмера наружных размеров тела; в этом случае необходимо учитывать толщину ножек штангенциркуля, которая указывается на самом инструмента. Некоторые штангенциркули снабжаются линейкой 5, служащей для измерения глубин. В лабораторной практике широко используются также круговые нониусы в различных приборах для измерения углов. Микрометр
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот процесс совершается через равные промежутки времени, то колебание называется периодическим. Несмотря на большое разнообразие колебательных процессов как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими, которые совершаются по закону синуса (или косинуса). Предположим, что они описываются законом
Здесь x - смещение (отклонение) колеблющейся системы от положения равновесия; А - амплитуда, т.е. максимальное смещение от положения равновесия, φо - начальная фаза колебания (при t=0); t - время колебаний; ω - круговая частота (или угловая скорость) колебаний. ω связана с частотой колебания Т - период - время одного полного колебания.
Систему, закон движения которой имеет вид (1), называют одномерным классическим гармоническим осциллятором. Хорошо известным примером гармонического осциллятора является тело (шарик), подвешенное на упругой пружине. По закону Гука при растяжении или сжатии пружины возникает противодействующая сила, пропорциональная растяжению или сжатию х, т.е. тело будет совершать гармонические колебания под действием силы упругости пружины F=-kx. Однако гармонические колебания возникают под действием не только упругих, но и других сил, по природе не упругих, но для которых остается справедливым закон F=-kx. Такие силы получили название квазиупругих. Как известно, движение системы под действием силы описывается II-м законом Ньютона: ma =F, где a - ускорение колеблющейся системы Для гармонических колебаний F=-kx. Тогда второй закон Ньютона будет иметь вид неполного дифференциального уравнения второго порядка
или уравнение движения классического осциллятора, где Решением данного уравнения (3) является выражение (1), что нетрудно проверить, дифференцируя дважды (1) по времени и подставляя в уравнение (3). При этом получим, что Для упрощения записи в дальнейшем можно положить начальную фазу нулю (φо=0), тогда уравнение (1) будет иметь вид
Видно, что скорость при гармонических колебаниях тоже изменяется по гармоническому закону, но опережает смещение по фазе на Ускорение тела при гармонических колебаниях равно:
Сравнение этого выражения (6) с (1) показывает, что ускорение и смещение находятся в противофазе (рис.2). Это означает, что в тот момент, когда смещение достигает наибольшего положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Кинетическая энергия осциллятора при гармоническом колебании с учетом (4) и (5) имеет вид: Потенциальная энергия:
Полная энергия гармонического осциллятора в процессе колебаний не меняется. Действительно:
Из последнего выражения видно, что полная механическая энергия осциллятора пропорциональна квадрату амплитуды и не зависит от времени. Кинетическая и потенциальная энергии изменяются по гармоническому закону, как Рассмотрим некоторые из классических гармонических осцилляторов. Математический маятник
Если маятник отклонить от положения равновесия на небольшой угол α, то он начнет совершать колебания в вертикальной плоскости под действием составляющей силы тяжести Pt, которую называют тангенциальной составляющей (нормальная составляющая силы тяжести Pn будет уравновешиваться силой натяжения нити N). Из рис.3 видно, что тангенциальная составляющая силы тяжести Знак минус показывает, что сила, вызывающая колебательное движение, направлена в сторону уменьшения угла α. Если угол α мал, то синус можно заменить самим углом, тогда С другой стороны, из рис.3 видно, что угол α можно записать через длину дуги x и радиус ℓ: α = x/ℓ, т.е. сила, возвращающая маятник в положение равновесия, является квазиупругой: С учетом (4), можно записать, что Период колебаний математического маятника при малых углах отклонения не зависит от амплитуды колебания и от его массы, а определяется длиной маятника и ускорением свободного падения g. Физический маятник
На рис.4 изображено сечение физического маятника плоскостью, перпендикулярной к его оси вращения О и проходящей через его центр тяжести С. Запишем в общем виде уравнение движения маятника, т.е. основное уравнение динамики вращательного движения M = Jβ, (9) где J - момент инерции маятника относительно горизонтальной оси О, β - угловое ускорение, М - момент внешних сил. В нашем случае момент внешних сил обусловлен действием силы тяжести. Очевидно, что на каждый элемент массы Δ mi маятника действует сила тяжести Δ mig, создающая определенный момент относительно оси О. Сумма моментов этих сил равна моменту равнодействующей сил тяжести, которая приложена к центру тяжести маятника (точка С). Докажем, что маятник, выведенный из положения равновесия на малый угол φ, будет совершать гармонические колебания. Для этого равнодействующую сил тяжести P=mg разложим на две составляющие, одна из которых P2 уравновешивается реакцией опоры, а под действием другой составляющей P1=Psinφ маятник приходит в движение. Обозначим расстояние от точки подвеса О до центра тяжести С через a. Тогда уравнение движения маятника (9) запишется в виде Jβ=-P1·a=-P·a·sinφ. (10) Знак минус показывает, что сила P1 направлена к положению равновесия и приводит к уменьшению угла отклонения φ. Так как
Частным решением этого дифференциального уравнения является уравнение
Величина Физическим маятником также можно воспользоваться для определения ускорения свободного падения. Любой физический маятник обладает свойством сопряженности, которое заключается в том, что в нем можно найти такие две точки, что при последовательном подвешивании маятника за ту или иную из них, период колебаний его остается одним и тем же. Расстояние между этими точками определяет собой приведенную длину физического маятника. Разновидностью физического маятника является оборотный маятник, который обладает свойством сопряженности центра качания и точки подвеса. Центром качания называется точка, находящаяся на расстоянии приведенной длины РАБОТА N 2-1 С ЭЛЕКТРОННЫМ СЕКУНДОМЕРОМ Приборы и принадлежности: установка, состоящая из двух маятников –математического и оборотного, масштабная линейка. Описание экспериментальной установки Общий вид установки представлен на рис. 5 Основание 1 оснащено регулируемыми ножками 2, которые позволяют провести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с фотоэлектрическим датчиком 6. После отвинчивания винта 11 верхний кронштейн можно поворачивать вокруг колонки. Затягивание винта 11 фиксирует кронштейн в любом, произвольно избранном положении. С одной стороны кронштейна 4 находится математический маятник 7, с другой оборотный маятник 8. Длину математического маятника можно регулировать при помощи винта 9, ее величину определять при помощи шкалы на колонке 3.
Нижний кронштейн 5 вместе с фотоэлектрическим датчиком 6 можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Когда колеблющийся маятник (математический или оборотный) пересекают световой луч, падающий на фототранзистор, то в цепи фототранзистора генерируются электрические импульсы. Специальная электронная схема считает число импульсов и выдает на световой индикатор информацию о числе полных колебаний маятника. Одновременно электронный секундомер 10 ведет отсчет времени и результат фиксируется на световом индикаторе. Схема управления осуществляет синхронное включение и выключение счетчика колебаний и секундомера. Зная число колебаний маятника и время, за которое они совершаются, можно определить период колебания маятника. Выполнение работы Проверьте, заземлен ли прибор. Включите сетевой шнур в сеть 220 В. Нажмите выключатель «СЕТЬ», при этом индикаторы измерителя показывают нуль и горит лампочка фотоэлектрического датчика. Прибор готов к работе. Упражнение 1. Изучение законов колебательного движения математического маятника и определение ускорения свободного падения. Нижний кронштейн вместе с фотоэлектрическим датчиком установите на отметке 50 см. Затяните винт, фиксируя фотоэлектрический датчик в избранном положении. С помощью верхнего кронштейна поместите над датчиком математический маятник. Вращая винт на верхнем кронштейне, опустите шарик математического маятника до нижнего кронштейна, обращая внимание, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика. Таким образом устанавливается длина математического маятника. 1. Проверка зависимости периода колебаний от его длины и амплитуды. Для этого приведите маятник в колебательное движение, отклонив шарик от положения равновесия на 4–50. Нажмите кнопку «СБРОС». После отсчета измерителем 15-20 полных колебаний нажмите кнопку «СТОП». Определите период колебаний маятника по формуле T=t/n, где n – число колебаний, t – показание электронного секундомера. Измерения периода проводятся не менее трех раз. Изменяя длину маятника на 2-3 см в одну и другую сторону, проведите аналогичные измерения для других длин маятника. Данные измерений занесите в таблицу.
Не меняя длину маятника, определите периоды колебания маятника при разных амплитудах колебания А. Измерения также проводятся не менее трех раз для каждой амплитуды. Составьте таблицу, аналогичную предыдущей, и все данные занесите в эту таблицу. Сделайте вывод, как зависит период колебаний математического маятника от его длины и амплитуды. 2. Используя имеющиеся усредненные данные для периода колебаний, по формуле (8) определите ускорение свободного падения g. С целью оценки погрешности g выведите формулу для расчета абсолютной и относительной ошибки измерения и определите их (D l=2мм, а DТ берется из эксперимента). Упражнение 2. Определение ускорения свободного падения при помощи оборотного маятника. Положение на стержне физического маятника чечевиц и одной из опорных приз П2 указывается преподавателем. Крепление всех деталей на стержне следует производить очень тщательно, добиваясь, чтобы зажимные винты входили в канавки на стержне. При изменении положения чечевицы или опорных призм маятник надо снять с кронштейна, положить на стол и провести перемещения чечевиц или призмы. Установите маятник на призму П1. Нижний кронштейн вместе с фотоэлектрическим датчиком переместите таким образом, чтобы стержень маятника пересекал оптическую ось датчика. Отклоните маятник на 4-50< |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.186.109 (0.019 с.) |

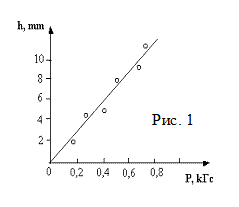 Экспериментальные точки следует наносить с максимальной точностью так, чтобы они четко выделялись на фоне графика, не сливаясь с ним.
Экспериментальные точки следует наносить с максимальной точностью так, чтобы они четко выделялись на фоне графика, не сливаясь с ним. Нониусы бывают линейные и круговые, прямые и обратные, нерастянутые и растянутые.
Нониусы бывают линейные и круговые, прямые и обратные, нерастянутые и растянутые. .
.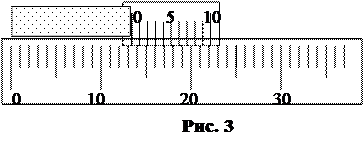 Длина отрезка, измеряемая при помощи нониуса, будет равна числу целых делений масштаба до нуля нониуса плюс точность нониуса, умноженная на номер его деления, совпадающего с некоторым делением масштаба. На рис.3 длина тела равна 13 – ти целым и 3-м десятых, так как совпадает с делениями масштаба 3 – е деление нониуса.
Длина отрезка, измеряемая при помощи нониуса, будет равна числу целых делений масштаба до нуля нониуса плюс точность нониуса, умноженная на номер его деления, совпадающего с некоторым делением масштаба. На рис.3 длина тела равна 13 – ти целым и 3-м десятых, так как совпадает с делениями масштаба 3 – е деление нониуса. . Таким образом, можно сказать, что погрешность нониуса равна половине его точности.
. Таким образом, можно сказать, что погрешность нониуса равна половине его точности. Круговой нониус в принципе ничем не отличается от линейного. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга лимба, разделенного на градусы или на доли градуса (рис. 4). Точность кругового нониуса обычно выражается в минутах. Часто круговые нониусы в приборах, в которых необходимо отсчитать углы в обоих направлениях (по часовой стрелке или против нее), состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нуля
Круговой нониус в принципе ничем не отличается от линейного. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга лимба, разделенного на градусы или на доли градуса (рис. 4). Точность кругового нониуса обычно выражается в минутах. Часто круговые нониусы в приборах, в которых необходимо отсчитать углы в обоих направлениях (по часовой стрелке или против нее), состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нуля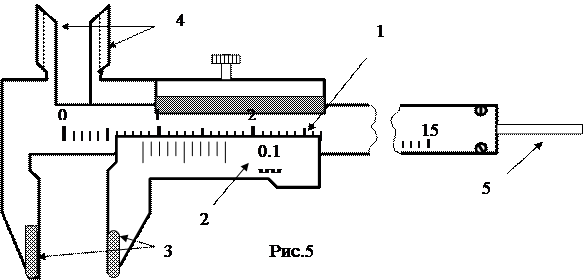 Штангенциркуль
Штангенциркуль Микрометр (рис.6) служит для измерений диаметров проволок, небольших толщин пластинок и т.п. Он имеет вид тисков и при измерении предмет зажимается между неподвижным стержнем 1 и подвижным торцом микрометрического винта 2. Микровинт вращают, держась за трещетку 3. На стержне микровинта укреплен барабан 4, с нанесенной на нем шкалой, имеющей 50 делений. Отсчет ведется по горизонтальной шкале 5 и по шкале барабана. Ход винта (поступательное перемещение барабана и стержня 2 при совершении одного оборота винта) равен 0,5 мм. Это означает, что цена деления барабана 0,01 мм. Следует обратить внимание, что выше основной миллиметровой шкалы имеется дополнительная линейная шкала, смещенная относительно основной на 0,5 мм.
Микрометр (рис.6) служит для измерений диаметров проволок, небольших толщин пластинок и т.п. Он имеет вид тисков и при измерении предмет зажимается между неподвижным стержнем 1 и подвижным торцом микрометрического винта 2. Микровинт вращают, держась за трещетку 3. На стержне микровинта укреплен барабан 4, с нанесенной на нем шкалой, имеющей 50 делений. Отсчет ведется по горизонтальной шкале 5 и по шкале барабана. Ход винта (поступательное перемещение барабана и стержня 2 при совершении одного оборота винта) равен 0,5 мм. Это означает, что цена деления барабана 0,01 мм. Следует обратить внимание, что выше основной миллиметровой шкалы имеется дополнительная линейная шкала, смещенная относительно основной на 0,5 мм. Прежде чем пользоваться микрометром, необходимо убедиться, что микрометр исправлен – нули его шкал совпадают. Измеряемый предмет помещают между стержнем 1 и винтом 2. Затем, вращая винт за головку 3, доводят его до соприкосновения с предметом. Момент зажатия фиксируется треском. После этого треска дальнейшее вращение головки 3 бесполезно, а барабана 4 недопустимо. Отсчет производят по шкалам: миллиметры по основной линейной шкале, доли миллиметра по шкале на барабане. При отсчете необходимо учитывать, появилась ли половинка деления верхней шкалы после последнего перед краем барабана деления нижней основной шкалы или нет. На рис.7 крупным планом показаны шкалы микрометра. Как видно из рис.7 (слева), когда край барабана перешел нижнюю риску, соответствующую 6,00 мм, а риска верхней шкалы не видна, то длина измеряемого предмета равна 6,15 мм. Когда же край барабана перешел верхнюю риску (рис.7, справа), соответствующую 6,50 мм, то длина измеряемого предмета равна 6,65 мм. Нетрудно понять, что цена деления барабана, равная 0,01 мм, и является точностью прибора, которая указывается на микрометре.
Прежде чем пользоваться микрометром, необходимо убедиться, что микрометр исправлен – нули его шкал совпадают. Измеряемый предмет помещают между стержнем 1 и винтом 2. Затем, вращая винт за головку 3, доводят его до соприкосновения с предметом. Момент зажатия фиксируется треском. После этого треска дальнейшее вращение головки 3 бесполезно, а барабана 4 недопустимо. Отсчет производят по шкалам: миллиметры по основной линейной шкале, доли миллиметра по шкале на барабане. При отсчете необходимо учитывать, появилась ли половинка деления верхней шкалы после последнего перед краем барабана деления нижней основной шкалы или нет. На рис.7 крупным планом показаны шкалы микрометра. Как видно из рис.7 (слева), когда край барабана перешел нижнюю риску, соответствующую 6,00 мм, а риска верхней шкалы не видна, то длина измеряемого предмета равна 6,15 мм. Когда же край барабана перешел верхнюю риску (рис.7, справа), соответствующую 6,50 мм, то длина измеряемого предмета равна 6,65 мм. Нетрудно понять, что цена деления барабана, равная 0,01 мм, и является точностью прибора, которая указывается на микрометре. (1)
(1) - фаза колебаний. Физический смысл фазы в том, что она определяет смещение х в данный момент времени,
- фаза колебаний. Физический смысл фазы в том, что она определяет смещение х в данный момент времени, и периодом колебания Т:
и периодом колебания Т: 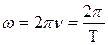 , (2)
, (2) Если в уравнении (1) положить начальную фазу φо =0, то график зависимости смещения х от времени или график гармонического колебания будет иметь вид, представленный на рис.1.
Если в уравнении (1) положить начальную фазу φо =0, то график зависимости смещения х от времени или график гармонического колебания будет иметь вид, представленный на рис.1.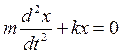 , (3)
, (3) .
. (4)
(4) (1΄)
(1΄) Скорость гармонически колеблющегося тела можно найти, дифференцируя по времени уравнение (1΄):
Скорость гармонически колеблющегося тела можно найти, дифференцируя по времени уравнение (1΄): или
или  . (5)
. (5) (по времени на Т/4).
(по времени на Т/4). , или
, или (6)
(6)
 , а так как "k" связано с собственной частотой колебания осциллятора (
, а так как "k" связано с собственной частотой колебания осциллятора (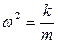 ), то
), то

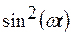 и
и  , но когда одна из них увеличивается, другая уменьшается. Это означает, что процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно.
, но когда одна из них увеличивается, другая уменьшается. Это означает, что процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Математическим маятником называют систему, состоящую из невесомой и нерастяжимой нити, на которой подвешен шарик, масса шарика сосредоточена в одной точке (рис.3). В положении равновесия на шарик действуют две силы: сила тяжести P=mg и сила натяжения нити N - равные по величине и направленные в противоположные стороны.
Математическим маятником называют систему, состоящую из невесомой и нерастяжимой нити, на которой подвешен шарик, масса шарика сосредоточена в одной точке (рис.3). В положении равновесия на шарик действуют две силы: сила тяжести P=mg и сила натяжения нити N - равные по величине и направленные в противоположные стороны. .
. .
. , где
, где 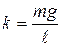 - коэффициент квазиупругой силы. Второй закон Ньютона в этом случае будет иметь следующий вид:
- коэффициент квазиупругой силы. Второй закон Ньютона в этом случае будет иметь следующий вид: 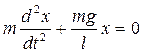 . (7)
. (7) , откуда
, откуда  . (8)
. (8)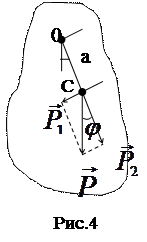 Физическим маятником называется абсолютно твердое тело, которое может совершать колебания под действием силы тяжести вокруг горизонтальной оси О, перпендикулярной плоскости рисунка и не проходящей через его центр тяжести.
Физическим маятником называется абсолютно твердое тело, которое может совершать колебания под действием силы тяжести вокруг горизонтальной оси О, перпендикулярной плоскости рисунка и не проходящей через его центр тяжести.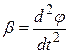 , а для малых углов φ можно принять sinφ≈φ, то уравнение (10) будет иметь вид:
, а для малых углов φ можно принять sinφ≈φ, то уравнение (10) будет иметь вид: , или
, или  . (11)
. (11) , где
, где 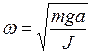 . Исходя из полученного выражения для ω, находим выражение для периода колебаний физического маятника
. Исходя из полученного выражения для ω, находим выражение для периода колебаний физического маятника . (12)
. (12) называется приведенной длиной физического маятника, это есть длина эквивалентного математического маятника, имеющего тот же период колебаний, что и данный физический маятник.
называется приведенной длиной физического маятника, это есть длина эквивалентного математического маятника, имеющего тот же период колебаний, что и данный физический маятник. от оси вращения. Приведенная длина всегда больше величины a (см.рис.4), т.е. центр качания всегда лежит ниже центра тяжести. Действительно, по теореме Штейнера момент инерции маятника относительно оси вращения равен J=Jo+ma2, где Jo - момент инерции маятника относительно оси, проходящей через центр тяжести. Тогда приведенная длина ℓ пр равна
от оси вращения. Приведенная длина всегда больше величины a (см.рис.4), т.е. центр качания всегда лежит ниже центра тяжести. Действительно, по теореме Штейнера момент инерции маятника относительно оси вращения равен J=Jo+ma2, где Jo - момент инерции маятника относительно оси, проходящей через центр тяжести. Тогда приведенная длина ℓ пр равна  , т.е.
, т.е.  >a.
>a.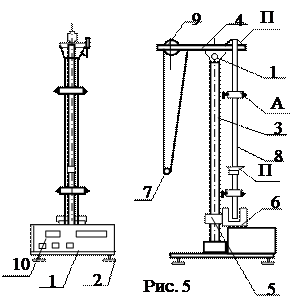 Оборотный маятник выполнен в виде стального стержня 8, на котором могут перемещаться и закрепляться в различных положения две опорные призмы П1 и П2 и тяжелые чечевицы А1 и А2. Используемый в работе маятник позволяет перемещать опорную призму только через 10 мм. На таком расстоянии друг от друга на стержне нанесены кольцевые канавки. С их помощью положение чечевиц и опорных призм фиксируется на стержне зажимными винтами. Т.к. расстояние между призмами изменяется не непрерывно, а через 10 мм, то при определении приведенной длины маятника добиться совпадения периодов маятника Т1 и Т2 (см. ниже) невозможно.
Оборотный маятник выполнен в виде стального стержня 8, на котором могут перемещаться и закрепляться в различных положения две опорные призмы П1 и П2 и тяжелые чечевицы А1 и А2. Используемый в работе маятник позволяет перемещать опорную призму только через 10 мм. На таком расстоянии друг от друга на стержне нанесены кольцевые канавки. С их помощью положение чечевиц и опорных призм фиксируется на стержне зажимными винтами. Т.к. расстояние между призмами изменяется не непрерывно, а через 10 мм, то при определении приведенной длины маятника добиться совпадения периодов маятника Т1 и Т2 (см. ниже) невозможно. 3
3










 Cp
Cp



