
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента поверхностного натяженияжидкости методом компенсации дополнительного давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приборы и принадлежности: прибор для определения коэффициента поверхностного натяжения, измерительный микроскоп, набор капилляров. Краткая теория
перпендикулярно ее поверхности (рис.1). Величина этой силы растет в направлении от внутренней к наружной границе поверхностного слоя жидкости. Таким образом, в поверхностном слое жидкости обнаруживается нескомпенсированность молекулярных сил: частицы жидкости, находящиеся в этом слое, испытывают направленную внутрь силу притяжения остальной частью жидкости. Поэтому поверхностный слой жидкости оказывает на нее большое внутреннее давление, достигающее десятков тысяч атмосфер. Это давление называется внутренним или молекулярным. Переход молекулы из глубины жидкости в поверхностный слой связан с совершением работы против действующих в поверхностном слое сил. Эта работа совершается молекулой за счет запаса ее кинетической энергии и идет на увеличение потенциальной энергии молекулы. При обратном переходе молекулы внутрь жидкости потенциальная энергия, которой обладала молекула в поверхностном слое, переходит в кинетическую энергию молекулы. Таким образом, молекулы в поверхностном слое обладают дополнительной потенциальной энергией, а поверхностный слой в целом обладает дополнительной энергией W, которая входит составной частью во внутреннюю энергию жидкости. Поскольку энергия W обязана своим происхождением наличию поверхности, то она должна быть пропорциональна площади S этой поверхности: W = α· S, (1) где a - коэффициент поверхностного натяжения. Коэффициент поверхностного натяжения численно равен работе, которую надо совершить для увеличения поверхности жидкости на единицу площади. Его величина зависит от природы жидкости, от наличия в ней примесей и от температуры. Поскольку с повышением температуры различие в плотностях жидкости и ее насыщенного пара уменьшается, то при этом уменьшается и коэффициент поверхностного натяжения. При критической температуре a обращается в нуль.
Физический смысл коэффициента a можно определить иначе. Поскольку всякая система в состоянии равновесия имеет минимальную энергию, то очевидно, из-за наличия поверхностной энергии жидкость в своем стремлении к равновесию стремится сократить свою поверхность до минимума. Жидкость ведет себя так, как если бы она была заключена в упругую растянутую пленку, стремящуюся сжаться. Следовательно, должны существовать силы, препятствующие увеличению поверхности жидкости, стремящиеся сократить ее. Они должны быть направлены вдоль самой поверхности, по касательной к ней. Эти силы называются силами поверхностного натяжения. Они возникают вследствие стремления жидкости уменьшить свою поверхность, а следовательно, и поверхностную энергию. Однако первопричиной возникновения сил поверхностного натяжения следует считать силы, действующие на молекулы поверхностного слоя и направленные внутрь жидкости. Пусть поверхностный слой занимает часть рамки, как показано на рис.2. Этот слой стремится сократить свою поверхность. Если участок АВ рамки может свободно перемещаться, то при сокращении поверхности эта сторона переместится влево на расстояние dx, что соответствует изменению площади поверхности на Совершаемая при этом работа равна:
С другой стороны, Отсюда сила поверхностного натяжения F, сокращающая поверхность жидкости, равна: Формула (4) дает второе определение коэффициента поверхностного натяжения (вытекающее из первого): коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность. В соответствии с этим коэффициент a в ед.СИ измеряется в Н/м, а в системе СГС - в дн/см. Если поверхность жидкости не плоская, то стремление ее к сокращению приводит к возникновению давления, дополнительного по отношению к тому, которое испытывает жидкость с плоской поверхностью.
П. Лаплас нашел, что дополнительное давление
где R1 и R2 - радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности. Для сферической поверхности R1=R2=R и
Если силы взаимодействия между молекулами жидкости больше, чем между молекулами жидкости и твердого тела, то жидкость не смачивает твердое тело. Если же силы взаимодействия между молекулами жидкости меньше, чем между молекулами жидкости и твердого тела, то жидкость смачивает это твердое тело. При несмачивании в слое жидкости, который прилегает к твердому телу, результирующая сила направлена в сторону жидкости. Поверхность жидкости располагается перпендикулярно к силе и у вертикальной стенки располагается, как показано на рис.4а. Угол θ между касательными к поверхности жидкости и твердого тела называется краевым углом. В случае несмачивания краевой угол тупой (θ >90o). При смачивании в слое жидкости, который прилегает к твердому телу, результирующая сила направлена в сторону твердого тела. При этом угол θ <90о (острый) и поверхность жидкости располагается у вертикальной стенки, как показано рис.4б.
На рис.5 изображены два капилляра, опущенные в широкий сосуд с жидкостью. Если жидкость смачивает стенки капилляра, то ее поверхность внутри капилляра будет вогнутой, если не смачивает - выпуклой. Здесь R - радиус кривизны поверхности жидкости, r -радиус капилляра. Искривление поверхности ведет к появлению дополнительного давления, и жидкость в первом случае (
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 436; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.008 с.) |

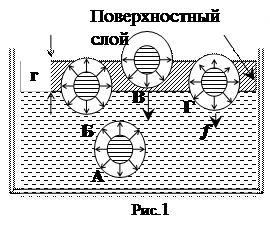 В жидкостях среднее расстояние между молекулами значительно меньше, чем в газах. Они располагаются настолько близко к друг к другу, что силы притяжения между ними имеют значительную величину. Поэтому взаимодействие между ними быстро убывает с расстоянием и можно считать, что каждая молекула взаимодействует лишь с теми молекулами, которые находятся внутри сферы определенного радиуса r с центром в данной молекуле (сфера молекулярного действия). Если молекулы, например, А и Б, находятся внутри жидкости (рис.1), то силы, действующие на них со стороны других молекул, взаимно компенсируются. Поскольку плотность пара гораздо меньше плотности жидкости, то на каждую молекулу, например В, находящуюся в поверхностном слое, действует сила f, направленная в глубь жидкости
В жидкостях среднее расстояние между молекулами значительно меньше, чем в газах. Они располагаются настолько близко к друг к другу, что силы притяжения между ними имеют значительную величину. Поэтому взаимодействие между ними быстро убывает с расстоянием и можно считать, что каждая молекула взаимодействует лишь с теми молекулами, которые находятся внутри сферы определенного радиуса r с центром в данной молекуле (сфера молекулярного действия). Если молекулы, например, А и Б, находятся внутри жидкости (рис.1), то силы, действующие на них со стороны других молекул, взаимно компенсируются. Поскольку плотность пара гораздо меньше плотности жидкости, то на каждую молекулу, например В, находящуюся в поверхностном слое, действует сила f, направленная в глубь жидкости Из формулы (1) следует, что коэффициент поверхностного натяжения a в ед.СИ измеряется в Дж/м2, а в системе СГС - в эрг/см2.
Из формулы (1) следует, что коэффициент поверхностного натяжения a в ед.СИ измеряется в Дж/м2, а в системе СГС - в эрг/см2. .
.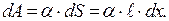 (2)
(2) (3)
(3)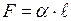 . (4)
. (4)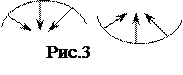 В случае выпуклой поверхности это давление положительно, а в случае вогнутой - отрицательно (рис.3).
В случае выпуклой поверхности это давление положительно, а в случае вогнутой - отрицательно (рис.3). , производимое на жидкость поверхностным слоем произвольной формы, равно:
, производимое на жидкость поверхностным слоем произвольной формы, равно: (5)
(5) (6)
(6) На форму поверхности жидкости, налитой в сосуд, влияет взаимодействие молекул жидкости с молекулами твердого тела.
На форму поверхности жидкости, налитой в сосуд, влияет взаимодействие молекул жидкости с молекулами твердого тела. Взаимодействие молекул жидкости с молекулами твердого тела ведет к искривлению поверхности жидкости вблизи стенок сосуда. В узких сосудах (капиллярах) влияние стенок распространяется на всю поверхность жидкости и она искривлена на всем своем протяжении. Такого рода изогнутые поверхности носят название менисков. Искривление поверхности жидкости приводит, как было показано выше, к появлению дополнительного давления. Непосредственным следствием этого дополнительного давления является капиллярный подъем (или опускание) жидкости.
Взаимодействие молекул жидкости с молекулами твердого тела ведет к искривлению поверхности жидкости вблизи стенок сосуда. В узких сосудах (капиллярах) влияние стенок распространяется на всю поверхность жидкости и она искривлена на всем своем протяжении. Такого рода изогнутые поверхности носят название менисков. Искривление поверхности жидкости приводит, как было показано выше, к появлению дополнительного давления. Непосредственным следствием этого дополнительного давления является капиллярный подъем (или опускание) жидкости.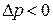 ) будет подниматься по капилляру, во втором (
) будет подниматься по капилляру, во втором ( ) - опускаться
) - опускаться


