
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование законов колебательного движенияСодержание книги
Поиск на нашем сайте
МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО НА УСТАНОВКЕ С ЭЛЕКТРОННЫМ СЕКУНДОМЕРОМ Приборы и принадлежности: установка, состоящая из двух маятников –математического и оборотного, масштабная линейка. Описание экспериментальной установки Общий вид установки представлен на рис. 5 Основание 1 оснащено регулируемыми ножками 2, которые позволяют провести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с фотоэлектрическим датчиком 6. После отвинчивания винта 11 верхний кронштейн можно поворачивать вокруг колонки. Затягивание винта 11 фиксирует кронштейн в любом, произвольно избранном положении. С одной стороны кронштейна 4 находится математический маятник 7, с другой оборотный маятник 8. Длину математического маятника можно регулировать при помощи винта 9, ее величину определять при помощи шкалы на колонке 3.
Нижний кронштейн 5 вместе с фотоэлектрическим датчиком 6 можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Когда колеблющийся маятник (математический или оборотный) пересекают световой луч, падающий на фототранзистор, то в цепи фототранзистора генерируются электрические импульсы. Специальная электронная схема считает число импульсов и выдает на световой индикатор информацию о числе полных колебаний маятника. Одновременно электронный секундомер 10 ведет отсчет времени и результат фиксируется на световом индикаторе. Схема управления осуществляет синхронное включение и выключение счетчика колебаний и секундомера. Зная число колебаний маятника и время, за которое они совершаются, можно определить период колебания маятника. Выполнение работы Проверьте, заземлен ли прибор. Включите сетевой шнур в сеть 220 В. Нажмите выключатель «СЕТЬ», при этом индикаторы измерителя показывают нуль и горит лампочка фотоэлектрического датчика. Прибор готов к работе. Упражнение 1. Изучение законов колебательного движения математического маятника и определение ускорения свободного падения. Нижний кронштейн вместе с фотоэлектрическим датчиком установите на отметке 50 см. Затяните винт, фиксируя фотоэлектрический датчик в избранном положении. С помощью верхнего кронштейна поместите над датчиком математический маятник. Вращая винт на верхнем кронштейне, опустите шарик математического маятника до нижнего кронштейна, обращая внимание, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика. Таким образом устанавливается длина математического маятника. 1. Проверка зависимости периода колебаний от его длины и амплитуды. Для этого приведите маятник в колебательное движение, отклонив шарик от положения равновесия на 4–50. Нажмите кнопку «СБРОС». После отсчета измерителем 15-20 полных колебаний нажмите кнопку «СТОП». Определите период колебаний маятника по формуле T=t/n, где n – число колебаний, t – показание электронного секундомера. Измерения периода проводятся не менее трех раз. Изменяя длину маятника на 2-3 см в одну и другую сторону, проведите аналогичные измерения для других длин маятника. Данные измерений занесите в таблицу.
Не меняя длину маятника, определите периоды колебания маятника при разных амплитудах колебания А. Измерения также проводятся не менее трех раз для каждой амплитуды. Составьте таблицу, аналогичную предыдущей, и все данные занесите в эту таблицу. Сделайте вывод, как зависит период колебаний математического маятника от его длины и амплитуды. 2. Используя имеющиеся усредненные данные для периода колебаний, по формуле (8) определите ускорение свободного падения g. С целью оценки погрешности g выведите формулу для расчета абсолютной и относительной ошибки измерения и определите их (D l=2мм, а DТ берется из эксперимента). Упражнение 2. Определение ускорения свободного падения при помощи оборотного маятника. Положение на стержне физического маятника чечевиц и одной из опорных приз П2 указывается преподавателем. Крепление всех деталей на стержне следует производить очень тщательно, добиваясь, чтобы зажимные винты входили в канавки на стержне. При изменении положения чечевицы или опорных призм маятник надо снять с кронштейна, положить на стол и провести перемещения чечевиц или призмы. Установите маятник на призму П1. Нижний кронштейн вместе с фотоэлектрическим датчиком переместите таким образом, чтобы стержень маятника пересекал оптическую ось датчика. Отклоните маятник на 4-50 от положения равновесия и дайте возможность ему совершать колебания. Нажмите кнопку “СБРОС” и после подсчета измерителем 15-20 полных колебаний нажмите кнопку “СТОП”. Определите период колебаний оборотного маятника по формуле T1=t1/n1, где n1 – число колебаний, t1 – показание электронного секундомера. Результаты заносятся в таблицу
Затем маятник снимается с кронштейна, переворачивается и устанавливается на призму П2. Снова определяются значения n 2, t 2 и вычисляются значения T 2. Измеряется и вносится в таблицу расстояние l между опорными призмами маятника. Переместите призму П2 на соседнее деление в таком направлении, чтобы Т 2 по своему значению приближался к значению Т 1. Определяют и заносят в таблицу новые значения l, n 2, t 2, T 2. Эти измерения повторяются до 4-5 раз пока значение периода Т 1 не попадет в «вилку» полученных значений Т 2 (значения Т 1 и Т 2 не должны отличаться более чем 0,5%). При равенстве Т 1 и Т 2 определите приведенную длину маятника, как расстояние между ребрами опорных призм и вычислите ускорение свободного падения по формуле (12). Используя соотношение (13), можно, зная l пр, массу маятника (m= 2,6 кг), определить момент инерции маятника J и величину а, т.е. положение центра тяжести мятника (см. Рис. 4). РАБОТА N 2-2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.006 с.) |

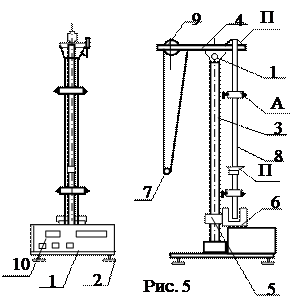 Оборотный маятник выполнен в виде стального стержня 8, на котором могут перемещаться и закрепляться в различных положения две опорные призмы П1 и П2 и тяжелые чечевицы А1 и А2. Используемый в работе маятник позволяет перемещать опорную призму только через 10 мм. На таком расстоянии друг от друга на стержне нанесены кольцевые канавки. С их помощью положение чечевиц и опорных призм фиксируется на стержне зажимными винтами. Т.к. расстояние между призмами изменяется не непрерывно, а через 10 мм, то при определении приведенной длины маятника добиться совпадения периодов маятника Т1 и Т2 (см. ниже) невозможно.
Оборотный маятник выполнен в виде стального стержня 8, на котором могут перемещаться и закрепляться в различных положения две опорные призмы П1 и П2 и тяжелые чечевицы А1 и А2. Используемый в работе маятник позволяет перемещать опорную призму только через 10 мм. На таком расстоянии друг от друга на стержне нанесены кольцевые канавки. С их помощью положение чечевиц и опорных призм фиксируется на стержне зажимными винтами. Т.к. расстояние между призмами изменяется не непрерывно, а через 10 мм, то при определении приведенной длины маятника добиться совпадения периодов маятника Т1 и Т2 (см. ниже) невозможно. 3
3










 Cp
Cp



