
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения из теории погрешностей измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§ 17. ПОГРЕШНОСТИ И ИХ ВИДЫ
Измерения в геодезии рассматриваются с двух точек зрения количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений. Если обозначить истинное значение измеряемой величины Х, а результат измерения l, то истинная погрешность измерения ∆= l – Х. Любая погрешность результата измерения есть следствие воздействия многих факторов, каждый из которых порождает свою погрешность. Погрешности, происходящие от отдельных факторов, называют элементарными. Погрешности результата измерения являются алгебраической суммой элементарных погрешностей. Изучением основных свойств и закономерностей действия погрешностей измерений, разработкой методов получения наиболее точного значения измеряемой величины и характеристик ее точности занимается теория погрешностей измерений. Излагаемые в ней методы решения задач позволяют рассчитать необходимую точность предстоящих измерений и на основании этого расчета выбрать соответствующие приборы и технологию измерений, а после производства измерений получить наилучшие их результаты и оценить их точность. Математической основой теории погрешностей измерений являются теория вероятностей и математическая статистика. Погрешности измерений разделяют по двум признакам: характеру их действия и источнику происхождения. По характеру действия погрешности бывают грубые, систематические и случайные. Грубыми называют погрешности, превосходящие по абсолютной величине некоторый установленный для данных условий измерений предел. Они происходят в большинстве случаев в результате промахов и просчетов исполнителя. Такие погрешности обнаруживают повторными измерениями, а результаты, содержащие их, бракуют и заменяют новыми. Погрешности, которые по знаку или величине однообразно повторяются в многократных измерениях (например, в длине линии из-за неточного знания длины мерного прибора, из-за неточности уложения мерного прибора в створе этой линии и т.п.), называют систематическими. Влияние систематических погрешностей стремятся исключить из результатов измерений или ослабить тщательной проверкой измерительных приборов, применением соответствующей методики измерений, а также введением поправок в результаты измерений. Случайными являются погрешности, размер и влияние которых на каждый отдельный результат измерения остаются неизвестными. Величину и знак случайной погрешности заранее установить нельзя. Однако теоретические исследования и многолетний опыт измерений показывают, что случайные погрешности подчинены определенным вероятностным закономерностям, изучение которых дает возможность получить наиболее надежный результат и оценить его точность. По источнику происхождения различают погрешности приборов, внешние и личные. Погрешности приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения. Внешние погрешности происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами. Личные погрешности связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей. Назад
§18. Свойства случайных погрешностей Случайные погрешности характeризуются следующими свойствами. 1. При определенных условиях измерений случайные погрешности по абсолютной величине не могут превышать известного предела, называемого предельной погрешностью. Это свойство позволяет обнаруживать и исключать из результатов измерений грубые погрешности. 2. Положительные и отрицательные случайные погрешности примерно одинаково часто встречаются в ряду измерений, что помогает выявлению систематических погрешностей. 3. Чем больше абсолютная величина погрешности, тем реже она встречается в ряду измерений. 4. Среднее арифметическое из случайных погрешностей измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании числа измерений стремится к нулю. Это свойство, называемое свойством компенсации, можно математически записать так: lim ([∆]/n) = 0, где [∆] – знак суммы, т.е. [∆] = ∆1 + ∆2 + ∆3 + ∙∙∙ + ∆n; n- число измерений. Последнее свойство случайных погрешностей позволяет установить принцип получения из ряда измерений одной и той же величины результата, наиболее близкого к ее истинному значению, т. е. наиболее точного. Таким результатом является среднее арифметическое из п измеренных значений данной величины. При бесконечно большом числе измерений lim([ l ]/n) = X. При конечном числе измерений арифметическая средина х = [ l ]/nсодержит остаточную случайную погрешность, однако от точного значения Х измеряемой величины она отличается меньше, чем любой результат l непосредственного измерения. Это позволяет при любом числе измерений, если n > 1, принимать арифметическую средину за окончательное значение измеренной величины. Точность окончательного результата тем выше, чем больше n. Назад
§19. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ, ПРЕДЕЛЬНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ Для правильного использования результатов измерений необходимо знать, с какой точностью, т. е. с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погрешностей служит предложенная Гауссом cредняя квадратическая погрешность т, вычисляемая по следующей формуле:
где n – число измерений данной величины. Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению, – арифметическую средину. Для этого случая средняя квадратическая погрешность одного измерения подсчитывается по формуле Бесселя:
где δ – отклонение отдельных значений измеренной величины от арифметической середины, называемые вероятнейшими погрешностями, причем [ δ ] = 0. Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая погрешность определяется по формуле.
M = m /
где т – средняя квадратическая погрешность одного измерения, вычисляемая по формулам (19.1) или (19.2). Часто в практике для контроля и повышения точности определяемую величину измеряют дважды – в прямом и обратном направлениях, например, длину линий, превышения между точками. Из двух полученных значений за окончательное принимается среднее из них. В этом случае средняя квадратическая погрешность одного измерения
а среднего результата из двух измерений
где d – разность двукратно измеренных величин; п – число разностей (двойных измерений). В соответствии с первым свойством случайных погрешностей для абсолютной величины случайной погрешности при данных условиях измерений существует допустимый предел, называемый предельной погрешностью. В строительных нормах предельная погрешность называется допускаемым отклонением. Теорией погрешностей измерений доказывается, что абсолютное большинство случайных погрешностей (68,3 %) данного ряда измерений находится в интервале от 0 до ± m; в интервал от 0 до ± 2m попадает 95,4%, а от 0 до ±3 m – 99,7% погрешностей. Таким образом, из 100 погрешностей данного ряда измерений лишь пять могут оказаться больше или равны 2 т, а из 1000 погрешностей только три будут больше или равны 3 т. На основании этого в качестве предельной погрешности ∆пр. для данного ряда измерений принимается утроенная средняя квадратическая погрешность, т. е. ∆пр.= 3 т. На практике во многих работах для повышения требований точности измерений принимают ∆пр. = 2 т. Погрешности измерений, величины которых превосходят ∆пр. считают грубыми. Иногда о точности измерений судят не по абсолютной величине средней квадратичной или предельной погрешности, а по величине относительной погрешности. Относительной погрешностью называется отношение абсолютной погрешности к значению самой измеренной величины. Относительную погрешность выражают в виде простой дроби, числитель которой – единица, а знаменатель – число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110м при ml = 2см равна ml/l = 1/5500, а относительная предельная погрешность при ∆пр. = 3т = 6см ∆пр./ l = 1/1800. Назад
§20. ОЦЕНКА ТОЧНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности. 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической средины х= [ l ]/п. 2. Вычисляют отклонения δi = l i – x каждого значения измеренной величины l 1, l 2, … l n от значения арифметической средины. Контроль вычислений: [δ] = 0. 3. По формуле Бесселя (19.2) вычисляют среднюю квадратическую погрешность одного измерения. 4. По формуле (19.3) вычисляют среднюю квадратическую погрешность арифметической середины. 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратичную погрешность каждого измерения и арифметической средины. 6. При необходимости подсчитывают предельную погрешность одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.
Таблица 20.1
Таблица 20.2
Примечание. Если в округляемом числе последняя цифра 5, то ее округляют до четной цифры, например: 10,375 - до 10,38; 0,245 - до 0,24.
Пример20.1. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в табл.20.1. Пример20.2. На метеостанции температура воздуха измерялась в разное время суток двумя одинаковыми термометрами. Требуется определить среднюю квадратичную погрешность измерения температуры воздуха одним термометром и среднего значения из одновременных измерений двумя термометрами. Значения измеренных температур воздуха и оценку точности измерений записывают по форме, приведенной в табл. 20.2. Оценку точности по разностям двукратных измерений производят в такой последовательности. 1. Вычисляют среднее значение из двукратных измерений. 2. Вычисляют разности d двукратных измерений. 3. По формуле (19.4) вычисляют среднюю квадратичную погрешность одного измерения 4,0см. По формуле (19.5) вычисляют среднюю квадратичную погрешность среднего результата из двух измерений.
Назад
§ 21. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ОШИБКА ФУНКЦИИ ИЗМЕРЕННЫХ ВЕЛИЧИН В тех случаях, когда пользуются косвенными методами измерений, ошибка результата зависит как от ошибок измеренных величин, так и действий, с помощью которых вычислен искомый результат. Поэтому определение ошибок функций измеренных величин mf имеет большое практическое значение. Рассмотрим функцию z самого общего вида от многих независимых величин l 1, l 2,…, l n:
z = f (l 1, l 2… l n). (21.1)
С учетом ошибок измерений, можно записать
z +Δz = f (l 1 + Δ l 1, l 2 + Δ l 2, … l n + Δ l n).
Поскольку Δ l 1, Δ l 2, …, Δ l n малы, то функцию можно разложить в ряд Тейлора, ограничиваясь членами, содержащими только первые степени ошибок Δ l 1, Δ l 2, … Δ l n. При разложении в ряд применяются частные производные, так как в уравнении имеются несколько переменных аргументов.
z + Δz = f (l 1, l 2, … l n) + ( откуда
Δz =
Для удобства записи примем, что
тогда уравнение (21.2) примет вид
Δz = K 1Δ l 1 + K 2Δ l 2 +… + K nΔ l n, (21.3)
где K 1, K 2, … K n – постоянные числа. Возведем уравнение (21.3) в квадрат и разделим на n
Если выполнен ряд измерений, то можно получить n аналогичных равенств, просуммировав которые можно получить уравнение
но так как
[Δ li Δ li+ 1] = 0, то
и учитывая, что
а
то
т.е. квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента.Назад РАЗДЕЛ 2
ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ ГЛАВА 5
ИЗМЕРЕНИЕ ДЛИНЫ ЛИНИЙ
§ 22. ВВОДНЫЕ СВЕДЕНИЯ Измерения – процесс сравнения какой-либо величины с другой одноименной величиной, принимаемой за единицу. Геодезические измерения позволяют определять относительное взаимное расположение отдельных точек земной поверхности. Геодезические измерения бывают: 1) линейными, в результате которых на местности определяются расстояния между заданными точками; 2) угловыми, определяющими значения горизонтальных и вертикальных углов на земной поверхности в данных вершинах между направлениями на некоторые заданные точки; 3) высотными (нивелирование), в результате которых определяются разности высот отдельных точек, т. е. разности расстояний по нормали от принятой отсчетной поверхности до данных точек. В России для перечисленных видов геодезических измерений используются следующие единицы: а) в линейных измерениях (горизонтальных и вертикальных) – метр. Эталон длины метра физически реализован в виде однометрового платино-иридиевого жезла № 28, хранящегося во Всероссийском научно-исследовательском институте метрологии; б) в угловых измерениях – окружность и ее доли – градус, равный 1/360 окружности; минута, равная 1/60 градуса; секунда, равная 1/60 минуты. В некоторых странах, например в ФРГ, применяется градовая (метрическая) система: 1 град, равный 1/400 окружности; 1 минута, равная 1/100 града; 1 секунда, равная 1/100 минуты. Измерение расстояний производят непосредственным или косвенным методами. При непосредственном методе мерный прибор (измерительную рулетку, землемерную ленту и т. п.) последовательно укладывают в створе измеряемого отрезка. При косвенном методе измеряют вспомогательные параметры (углы, базисы, физические параметры и т. п.), а длину отрезка вычисляют по формуле, отображающей зависимость между измеренными величинами и длиной отрезка. Непосредственно длины отрезков измеряются с помощью механических мерных приборов – мерных лент, рулеток, длинномеров и т. д. Косвенные методы реализуются с использованием различных видов дальномеров – оптических, радиофизических, лазерных и т. д. Точность определения расстояний зависит от метода измерений, применяемого прибора, условий измерений и колеблется от 1:200 до 1:1000 000 измеряемого расстояния. Назад
§ 23. механические мерные приборы Для непосредственного измерения линий на местности используют землемерные ленты со шпильками. В соответствии с ГОСТ 7502-80 такие ленты изготавливают длиной 20, 24, 50м и называют Л3-20, Л3-24 и Л3-50. Землемерные ленты изготавливают из стальной полосы, на концах которой прикреплены ручки (рис. 28, а, б). Длина ленты равна расстоянию между штрихами нанесенными у концов ленты против вырезов для шпилек. Метровые деления на лентах Л3-20 и Л3-50 обозначены пластинками с выбитыми на них порядковыми номерами, полуметровые деления отмечены круглыми заклепками, а дециметровые – отверстиями. Лента ЛЗ-24 разделена на 20 интервалов, а каждый интервал – на 10 равных частей. В комплект мерной ленты входят: лента, кольцо для ее наматывания и шпильки для фиксации концов ленты при измерениях.
Рис. 28. Землемерные ленты: а – при измерениях; б – на станке; 1 – штрих; 2 – вырез; 3 – заклепка; 4 – пластина; 5 – отверстие; 6 – линия, до которой выполнено измерение; 7 – ручка; в – стальная рулетка на крестовине; г - тесьмяная рулетка в футляре
Для измерения линий с повышенной точностью используют шкаловые ленты ЛЗШ-20, ЛЗШ-24 и ЛЗШ-50, длиной соответственно 20, 24 и 50м. У концов этих лент нанесены сантиметровые и миллиметровые деления. Длина шкаловой ленты равна расстоянию между нулевыми штрихами на концах ленты (рис.29).
Рис. 29. Лента землемерная шкаловая
Для измерения линий на строительных площадках и конструкциях здания обычно используют измерительные рулетки. В соответствии с ГОСТ 7502-80 отечественная промышленность изготавливает металлические рулетки ОПК2-20 AHT/I, ОПК2-30 AHT/1, ОПК2-50 АНТ/1 и др. Название рулетки ОПК2-20 АНТ/I означает, что рулетка в открытом корпусе (О), с плоской измерительной лентой (П), с вытяжным кольцом (К), 2-го класса точности, номинальной (стандартной) длины 20м. С началом, удаленным от торца измерительной ленты (А), с травлеными штрихами (Н), нанесенными через 1см (T/I). По дополнительным заказам предприятия изготавливают стальные рулетки на крестовине (рис. 28, в) с рукояткой для наматывания полотна рулетки на барабан. Некоторые фирмы в Японии выпускают металлические рулетки с пластиковым покрытием, что обеспечивает сохранность делений и предохраняет полотно от коррозии. Новейшие типы рулеток изготовлены на основе стекловолокна с пластиковым покрытием. Они менее чувствительны к воздействиям температуры, выдерживают натяжение силой более 1000 Ни не проводят электрического тока, что предохраняет их от сгорания при попадании на металлические конструкции при прогреве железобетона и при сварке. Для обмеров зданий и помещений внутри них, а также при измерениях небольших расстояний в некоторых видах съемочных и инженерно-геодезических работ используют тесьмяные рулетки в закрытом корпусе (рис. 28, г). Для измерений длин отрезков местности используют специальные приборы, которые называются длинномерами. Длиномер представляет собою мерный диск со счетным механизмом и направляющими роликами, который прокатывается по предварительно натянутой между измеряемыми точками проволоке. Таким образом, длиномером измеряется длина проволоки между конечными точками А и В линии. Мерный диск длиномера АД-l изготавливается из стали или инвара. Проектная длина окружности его канавки равна 300мм. Счетный механизм представляет собою типовой ступенчатый счетчик, связанный с мерным диском зубчатой передачей. Емкость счетчика равна 1000м. Считывание сантиметров и миллиметров производится по круговой шкале, скрепленной с диском, а метров, десятков и сотен метров – по счетному механизму. Примыкание к точкам обеспечивают два фиксатора. Длиномер удобен для измерений через овраги, ямы и т. п. В случае препятствий их обходят с длиномером, оттягивая проволоку в сторону. Если примыкание на конечной точке производится при натянутой в исходном положении проволоке, то такие обходы препятствий не вызывают погрешности в измерениях. На практике применяют также другие приборы и инструменты для непосредственного измерения линий, например: нутромеры – концевые меры со сферическими окончаниями для измерений и контроля расстояний контактным способом; катетометры – специальные приборы для измерений небольших (до 1м) вертикальных отрезков с очень большой точностью (0,006…0,050 мм); измерительные микроскопы, а также шаблоны и другие приспособления. Назад
§24. КОМПАРИРОВАНИЕ Под влиянием различных факторов (времени, температуры, механических воздействий и т. д.) длина мерного прибора изменяется. Поэтому перед началом и в конце полевого сезона, а также при повреждениях в процессе работы, мерные приборы компарируют, т. е. определяют их фактическую длину путем сравнения с эталоном. За эталоны принимают отрезки линий на местности, длины которых известны с высокой точностью. Такие приборы называются компараторами. Компараторы используют двух видов: стационарный – отрезок, закрепленный на местности специальными геодезическими знаками, длина которого известна высокой точностью. В производственных условиях мерные приборы чаще всего эталонируют на полевых компараторах. Такие компараторы представляют собой выровненные участки местности преимущественно с твердым покрытием. Концы компаратора закрепляют знаками со специальными метками, расстояние между которыми известно с большой точностью. Компарирование длинномерных рулеток и лент в полевых условиях производят на компараторах, длина которых, как правило, близка к l 0= 120м. Такую длину выбирают для того, чтобы уложить мерный прибор на компараторе несколько раз. Укладывание мерных приборов ведут в прямом и обратном направлениях. Подсчитывают число целых и дробных уложений рулетки или ленты и определяют поправку, обусловленную компарированием. Ее вычисляют по формуле
∆ l к = (l 0 – l ∑)/ n
где l ∑ – измеренная длина компаратора; l 0 – длина компаратора; п – число укладываний мерного прибора. Для предварительного компарирования или при желании знать фактическую длину вновь вводимого в эксплуатацию мерного прибора со сравнительно небольшой точностью поступают так. Нормальный мерный прибор (нормальным считается прибор, прошедший компарирование) и испытываемый укладывают на одну и ту же плоскость. Совмещают начальные штрихи, обе рулетки натягивают с одинаковой силой и миллиметровой линейкой измеряют расстояния между конечными штрихами. Измеренную величину считают поправкой вводимого в эксплуатацию мерного прибора по отношению к нормальному. Определение поправки в длину испытываемой рулетки производят после приведения длины нормальной и испытываемой рулеток к одной и той же температуре. На строительно-монтажной площадке часто приходится откладывать меньшую длину, чем длина рулетки. В этом случае проверяют длины метровых, дециметровых и более мелких делений. Компарирование мелких делений выполняют контрольной линейкой (нормальным метром), где минимальные отрезки нанесены через 0,2мм. Показания считывают через увеличительные стекла или микроскопы. Назад
§25. ИЗМЕРЕНИЕ ЛИНИЙ МЕРНЫМИ ПРИБОРАМИ
Измерение линий состоит в том, что мерный прибор (ленту, рулетку) последовательно откладывают между начальной и конечной точками измеряемой линии. Измерение производят в такой последовательности. Рекогносцировка, т. е. предварительное ознакомление с местностью. При рекогносцировке намечают на местности положение линий, подлежащих измерению. Линии стараются располагать так, чтобы условия для измерений были наиболее благоприятными. Вешение линии,т. е. установка вешек в створе линии. Створом называют вертикальную плоскость, проходящую через конечные точки линии. При подготовке створа линии к измерению ее концы фиксируют кольями, штырями, обрезками труб и т. д.; расчищают полосы шириной 1,5...2,0 м от растительности и остатков снесенных строений; забивают колья или штыри в местах перегибов местности. До измерения линию обозначают на местности (примерно через100м) вешками – деревянными или металлическими кругляками с равномерной яркой красно-белой окраской и заостренными концами. Вехи устанавливают либо «на глаз», либо с помощью оптической зрительной трубы с такой частотой, чтобы при нахождении мерщика у одной из них обеспечивалась видимость двух смежных. Вешение «на глаз» менее точно, чем с помощью оптической трубы с увеличением, однако его точность вполне достаточна, если измерение делать мерной лентой со шпильками. Вешение «на глаз» (рис. 30, а)выполняют приемами «от себя» и «на себя». При вешении «от себя» один мерщик становится на исходной точке, а на конечной точке второй мерщик устанавливает веху 7 такой высоты, чтобы она была видна с исходной точки. Второй мерщик по створу на расстоянии не более 100м от начала устанавливает веху 4, перемещая ее перпендикулярно створу до совпадения ее с вехой 7 на конечной точке. Команды о смещении устанавливаемой вехи в створ подают отмашкой руки.
Рис. 30. Вешение линии: а – профиль и план; б – измерение линии; 1,4,7 – вехи; 2,5 – шпильки; 3,6 – замеры
При вешении «на себя» мерщик выставляет вешку или укладывает мерную ленту в створе двух других вех, имея их перед собой. Измерение линии (рис. 30, б)выполняет бригада из двух человек. Ленту разматывают с кольца. Передний мерщик (МП) с десятью (пятью) шпильками протягивает передний конец ленты и по указанию заднего мерщика (МЗ) укладывает ее в створ измеряемой линии. Задний мерщик совмещает начальный штрих заднего конца ленты с началом линии, вставляя в вырез ленты шпильку. Передний мерщик встряхивает ленту, натягивает ее «от руки» силой около 98 Н и в вырез на переднем конце вставляет шпильку. Затем МЗ вынимает заднюю шпильку, МП снимает со шпильки ленту, и оба переносят ее вперед вдоль линии. Дойдя до первой шпильки, МЗ закрепляет на ней ленту, ориентирует МП, выставляя его руку со шпилькой и лентой в створ линии по передней вехе 7. Затем работа продолжается в том же порядке, что и на первом уложении ленты. Целое уложение ленты называется пролетом. Когда все 11(6) шпилек будут выставлены, у МЗ окажется 10 (5) шпилек. Задний мерщик передает переднему все собранные шпильки. Измеренный отрезок будет равен 10 l 0, что при 20-метровой длине ленты равно 200м. Число таких передач записывают в журнал измерений. Сюда же записывают результаты измерения неполного пролета: от последней шпильки в полном пролете до конечной точки линии. Для контроля линию измеряют вторично, при этом мерщики меняются местами, а за начало измерений принимают бывшую последней точку при измерении линии «прямо». Чтобы избежать грубых погрешностей при измерении, выполняют следующие действия: 1. подсчитывают, сколько шпилек у МЗ и МП, чтобы удостовериться, что в сумме они составляют комплект. 2. Следят, чтобы при измерении остатка отсчет выполнился от заднего конца ленты. 3. При отсчитывании делений на середине ленты следят, чтобы лента не быта перекручена, так как при этом можно спутать число целых метров. Например, вместо 6м отсчитать 9м, вместо 9 - 11м. Измеренную 20-метровой лентой длину линии D вычисляют по следующей формуле:
D = 200N + 20(п – 1) + r,
где N – число передач шпилек; п – число шпилек у М3; r – остаток. За окончательное значение принимают среднее арифметическое от измерений «прямо» и «обратно». Измерения считают выполненными правильно, если раcхождение результатов измерений «прямо» и «обратно» не превышают: 1:3000 от измеренной длины – при благоприятных условиях измерений (например, твердое покрытие); 1:2000 – при средних условиях измерений (например, ровная поверхность грунта); 1:1000 – при неблагоприятных условиях измерений (например, болотистая, кочковатая заросшая местность, снег и т. д.). Измерения линий рулеткой производят аналогично. Однако фиксация концов измеренных отрезков при работе рулеткой должна выполняться более точно (вешкой, иглами, остроотточенными карандашами и т. д.). Измерение линий шкаловыми лентами с повышенной точностью производят по кольям, которые вбивают в грунт под шкалами. Натяжение мерного прибора осуществляют силой 98 Н с помощью пружинного динамометра. Концы отрезков линии на кольях фиксируют булавками и производят отсчеты по передней (П) и задней (3) шкалам. После каждой пары отсчетов ленту сдвигают. В зависимости от требований к точности производят две или три пары отсчетов. О правильности отсчетов судят по разностям (П - 3). Сравнение значений длин отрезков, измеренных в прямом и обратном направлениях D пр и D обр позволяет обнаружить грубые промахи в измерениях, например, просчеты в целое число отложений мерного прибора. Назад
§26. ВЫЧИСЛЕНИЕ ДЛИНЫ ЛИНИИ При вычислении длин линий в результат измерения вводят поправки, которые исключают влияние систематических погрешностей. Поправка ∆ D к за компарирование мерного прибора. При измерении линий фактическая длина мерного прибора отличается от номинала на величину поправки за компарирование
r = r 0 + (∆к/ l 0) r 0 (26.1)
Аналогичное равенства можно записать для отрезка, чья длина кратна номинальной длине ленты l 0
D = n(l 0 + ∆ l к), (26.2)
где n – число целых мерных лент, отложенных в процессе измерения отрезка. Полная длина линии запишется как сумма (24.1) и (24.2)
D = n(l 0 + ∆ l к) + (r0 +
Раскроем скобки и перепишем формулу (24.3) в несколько ином виде D = (n l 0 + r 0) + Величина (n l0 + r 0) – эта длина линии, вычисленная с номинальным значением длины мерного прибора. Обозначив ее через D 0, запишем D = D 0 + (D 0/ l 0)∆ l к. Величину ∆ D к = D – D 0 = (D 0/ l 0)∆ l к называют поправкой в длину мерного прибора за компарирование.
Поправка ∆ D t за температуру мерного прибора. При измерении линий температура мерного прибора t обычно отличается от температуры компарирования t 0. В этом случае длина мерного прибора равна
l = l 0 + α(t – t 0) l 0 где α– коэффициент линейного расширения материала мерного прибора (для стали α= 12,5.10-6). Соответственно изменится длина остатка
r = r 0 + α(t – t 0) r 0. С учетом предыдущего соотношения получим уравнение, учитывающее поправку за температурное расширение прибора.
D = (n l 0 + r 0) + α (t – t 0) (n l 0 + r 0),
но n l 0 + r 0 = D 0, тогда
D = D 0 + α (t – t 0) D 0.
Величину
∆ Dt = D – D 0 = α(t – t 0) D 0.
называют поправкой в длину линии за температуру мерного прибора. Если при измерении линий для создания то
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.016 с.) |

 ,
,  (19.1)
(19.1) , (19.2)
, (19.2) (19.3)
(19.3) , (19.4)
, (19.4)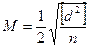 (19.5)
(19.5) см
M = 4,0/
см
M = 4,0/  = 1,6см
ml / l = 1/3000
M/ l = 1/7600
∆пр. = 12см
= 1,6см
ml / l = 1/3000
M/ l = 1/7600
∆пр. = 12см
 = 0,17 Сº
Mtср= 0,5
= 0,17 Сº
Mtср= 0,5  = 0,12 Cº
= 0,12 Cº
 ),
), . (21.2)
. (21.2) (i = 1, 2, …, n),
(i = 1, 2, …, n),
 (21.4)
(21.4) ,
,

 (21.5)
(21.5)




 r 0). (26.3)
r 0). (26.3) к. (26.4)
к. (26.4)


