
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геодезические разбивочные работыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§ 64. НАЗНАЧЕНИЕ И ОРГАНИЗАЦИЯ РАЗБИВОЧНЫХ РАБОТ
Проект сооружения составляют на топографических планах крупных масштабов. Определяют расположение проектируемого сооружения относительно окружающих предметов и сторон света. Кроме того, топографический план определяет общегеодезическую систему координат, задающую положение характерных точек проектируемого сооружения относительно этой системы.
Компоновка сооружения определяется его геометрией, которая, в свою очередь, задается осями. Относительно осей сооружения в рабочих чертежах указывают местоположение всех элементов сооружения.
Главными осями линейных сооружений (дорог, каналов, плотин, мостов и т. п.) служат продольные оси этих сооружений. В промышленном и гражданском строительстве в качестве главных осей принимают оси симметрии зданий (рис. 84). Основные оси определяют форму и габаритные размеры зданий и сооружений. Промежуточные, или детальные, оси – это оси отдельных элементов зданий, сооружений. На строительных чертежах оси проводят штрихпунктирными линиями и обозначают цифрами или буквами в кружках. Для обозначения продольных осей служат арабские цифры, а для поперечных осей – прописные буквы русского алфавита, за исключением букв 3, И, О, Х, Ы, Ъ, Ь. Оси обозначают слева направо и снизу вверх. Указанные в проекте сооружения координаты, углы, расстояния и превышения называют проектными. Высоты плоскостей и отдельных точек проекта задают от условной поверхности. В зданиях за условную поверхность (нулевую отметку) принимают уровень «чистого пола» первого этажа. Высоты относительно нулевой отметки обозначают следующим образом: вверх – со знаком «плюс», вниз – со знаком «минус». для каждого сооружения условная поверхность соответствует определенной абсолютной отметке, которая указывается в проекте. Весь процесс разбивки сооружения определяется общим геодезическим правилом перехода от общего к частному. Разбивка главных и основных осей определяет положение всего сооружения на местности, т. е. его размеры и ориентирование относительно сторон света и существующих контуров местности. Детальная разбивка определяет взаимное положение отдельных элементов и конструкций сооружения. Разбивочные работы – это комплексный взаимосвязанный процесс, являющийся неотъемлемой частью строительно-монтажного производства, поэтому организация и технология разбивочных работ целиком зависят от этапов строительства. В подготовительный период на местности строят плановую и высотную геодезическую разбивочную основу соответствующей точности, определяют координаты и отметки пунктов этой основы. Затем производится геодезическая подготовка проекта для перенесения его в натуру. Непосредственную разбивку сооружений выполняют в три этапа. На первом этапе производят основные разбивочные работы. По данным привязки от пунктов геодезической основы находят на местности положение главных или основных разбивочных осей и закрепляют их. На втором этапе, начиная с возведения фундаментов, проводят детальную строительную разбивку сооружений. От закрепленных точек главных и основных осей разбивают продольные и поперечные оси отдельных строительных элементов и частей сооружения, одновременно определяя уровень проектных высот. Детальная разбивка производится значительно точнее, чем разбивка главных осей, поскольку она определяет взаимное расположение элементов сооружения, а разбивка главных осей – лишь общее положение сооружения и его ориентирование. Если главные оси могут быть определены на местности со средней квадратической погрешностью 3–5 см, а иногда и грубее, то детальные оси разбивают со средней квадратической погрешностью 2– 3мм и точнее. Третий этап заключается в разбивке технологических осей оборудования. На этом этапе требуется наибольшая точность (в отдельных случаях – доли миллиметра). Разбивочные работы состоят из совокупности геодезических операций, называемых элементами геодезических разбивочных работ. Отдельные виды и этапы разбивочных работ являются сочетанием тех или иных элементов. Назад
§ 65. ОСНОВНЫЕ ЭЛЕМЕНТЫ РАЗБИВОЧНЫХ РАБОТ К элементам разбивочных работ относятся следующие виды натурных измерений. 1.Построение на местности проектного значения горизонтального угла. 2.Вынос в натуру отрезка проектной длины. 3.Построение точки с заданной проектной отметки. 4.Построение на местности линии заданного уклона. 5.Построение на местности плоскости с заданным уклоном.
Стандартные геодезические приборы, изготовленные серийно, по точности предназначены для выполнения измерений, а не построений. В результате точность отложения разбивочных элементов этими приборами оказывается ниже, чем точность измерений с использованием этих приборов. Поэтому, если необходимо построить проектный угол с повышенной точностью, поступают следующим образом: построенный в натуре угол измеряют несколькими приемами и определяют его более точное значение β'. Измерив построенный в натуре угол, вычисляют поправку
Δ β = β ' - β,
которую необходимо ввести для уточнения построенного угла. Зная проектное расстояние ВС = ℓ, вычисляют линейную поправку СС' = М. Из геометрии построений (см. рис. 85) следует, что
где β и ρ выражены в секундах; ρ – число секунд в радиане. Затем откладывают от точки С перпендикулярно линии ВС величину вычисленной поправки Δℓ и фиксируют точку С'. Угол АВС' и будет равен проектному углу с заданной точностью. Для контроля угол АВС' измеряют. Если полученное значение отличается от проектного на допускаемую величину, то работу заканчивают. В противном случае требуется дальнейшее уточнение. Точность построения на местности проектного угла зависит от инструментальных погрешностей, погрешностей собственно измерения (визирования и отсчета по лимбу), а также погрешностей из-за влияния внешних условий. Погрешности центрирования, редукции и исходных данных (погрешности в положении пунктов А и В)на точность отложения проектного угла влияния не оказывают, что позволяет учитывать их отдельно. В этом заключается еще одна особенность разбивочных работ. Однако эти погрешности вызывают смещение на местности направления ВС и выносимой точки С. Необходимая точность отложения линейной поправки (редукции) Δℓ составляет примерно 2мм. Очевидно, что с такой точностью линейную редукцию можно легко отложить при помощи рулетки или линейки с миллиметровыми делениями. Построение на местности линий заданной длины является наиболее распространенной при разбивочных работах задачей. Подлежащая отложению длина линии задается горизонтальным проложением; в общем случае требуется отложить соответствующее ему расстояние на наклонной топографической поверхности. Задача решается при помощи ленты или рулетки двумя способами: а) непосредственное отложение заданной длины на заранее подготовленной горизонтальной поверхности; б) отложение отрезка заданной длины с последующим перемещением конечной точки отрезка на величину поправки за наклон местности. При применении обоих способов вводят поправки за компарирование мерного прибора и за разность температур компарирования и измерения (формулы поправок см. § 26). При применении второго способа в непосредственное измерение на местности вводят поправку за наклон (см. § 26), но собратным знаком. Поправку за компарирование вводят со знаком плюс, если мерный прибор короче своего номинального значения, и со знаком минус, если он длиннее. Эта поправка определяется с точностью 1:20000, т. е. 1мм на 20м. Поправку за температуру вводят со знаком плюс, если температура отложения линии ниже температуры компарирования, и наоборот. Второй способ более общий, имеет большее распространение и точность. Практически на местности откладывают мерный прибор d целое число раз и получают две точки М 1и М 2(рис.86), между которыми должна находиться конечная точка С откладываемого расстояния.
Рис. 86. Разбивка линии заданной длины
После введения всех поправок в расстояния АМ 1 и АМ 2 определяют длины отрезков а и d – а и, откладывая от М 1 отрезок а,а от М 2 – отрезок d – a, предварительно определяют положение точки С. В месте расположения точки С закладывают монолит с металлической пластиной размером 150 х 150мм, на которой и фиксируют точку С. Далее расстояние АС измеряют с установленной точностью и получают длину отложенной линии. Сравнивая ее значение с заданной длиной, находят поправку СС l, которую откладывают, пользуясь измерителем и масштабной линейкой, на пластине и окончательно фиксируют конечную точку заданного отрезка АС. Этот способ построения отрезка называется способом редукции. Для расстояния АС ≈200м при центрировании теодолита и визирных целей с помощью оптического отвеса ошибка за поперечное смещение в длине отложенной линии будет около ±2,5мм;при АС = 400м она соответственно равна ±5мм. При применении нитяного отвеса ошибки для тех же расстояний будут соответственно ±3,0 и ±6мм. Вынос в натуру проектных отметок. Все отметки, указанные в проекте сооружения, даются от уровня «чистого пола» или какого-либо другого условного уровня, поэтому предварительно их необходимо пере вычислить в систему, в которой даны высоты исходных реперов. Для выноса в натуру точки с проектной отметкой Н пр устанавливают нивелир примерно посередине между репером с известной отметкой Н ри выносимой точкой (рис. 87). На исходном репере и выносимой точке устанавливают рейки, взяв отсчет а по рейке на исходном репере, определяют горизонт прибора
Н ГП = Н р + а.
Для контроля желательно аналогичным образом проверить значение Н ГП по другому исходному реперу. Чтобы установить точку на проектную отметку Н ГП, необходимо знать величину отсчета b по рейке на определяемой точке. Можно записать, что
b = Н ГП – Н пр = Н р+ а – Н пр. Вычислив отсчет b, рейку в точке на проектной поверхности поднимают или опускают до тех пор, пока отсчет по среднему штриху зрительной трубы нивелира не будет равен вычисленному. В этот момент пятка рейки будет соответствовать проектной высоте. Ее фиксируют в натуре, забивая колышек, ввинчивая болт или проведя черту на строительной конструкции.
Рис. 87. Схема выноса в натуру проектной отметки
Для контроля, нивелируя обычным способом, определяют фактическую отметку вынесенной точки и сравнивают ее с проектной. В случае недопустимых расхождений работу выполняют заново. Если необходимо передать проектные отметки точек, лежащих в одной вертикальной плоскости (на стенах, колоннах и т. п.), то поступают следующим образом. На вертикальной плоскости отмечают проекцию среднего штриха сетки, т. е. фиксируют горизонт прибора. Затем, отмеряя вверх или вниз от этой линии соответствующее превышение, отмечают проектную отметку точки. Проектная отметка точки может быть установлена в натуре путем, аналогичным редуцированию. Для этого выносимую точку приближенно устанавливают на проектную высоту. Нивелированием определяют превышение h между приближенно установленной точкой и исходным репером. Полученную величину сравнивают с проектной h пр, вычисленной как h пр = Н пр – Н р. С учетом знака разности h пр – h изменяют высоту точки, добиваясь, чтобы h пр = h. Этот способ более трудоемкий и применяется, когда производят бетонирование до проектной отметки или поднимают конструкцию путем последовательного подбора подкладок. Для построения в натуре линий проектных уклонов используются нивелиры, теодолиты, а также лазерные приборы. Сначала конечные точки линии АВ (рис. 88) устанавливают на проектные отметки. Если дана отметка Н А только точки А и проектный уклон i, то отметку точки В можно вычислить по формуле
Н В = Н А + d i,
где d – проектное расстояние АВ.
Рис. 88. Схема построения линии заданного уклона с помощью нивелира
На точках А и В устанавливают нивелирные рейки. Затем, наклоняя нивелир двумя подъемными винтами (или элевационным винтом), методом приближений добиваются, чтобы отсчеты по рейкам стали одинаковыми и равными высоте инструмента. В этом случае визирная линия зрительной трубы нивелира будет иметь проектный уклон. Далее устанавливают визирку (рис. 88) или рейку в створе линии АВ (например, через d= 5м), добиваясь, чтобы отсчет по ней был равен отсчету на конечные точки. Пятка рейки будет определять точку линии проектного уклона. Эти точки фиксируют колышками соответствующей высоты. При использовании теодолита его устанавливают в начальной точке с проектной отметкой и измеряют высоту прибора (рис. 89).
Рис. 89. Схема выноса в натуру линии проектного уклона с помощью теодолита
На вертикальном круге с учетом места нуля устанавливают отсчет в градусной мере, равный проектному уклону. Линия визирования зрительной трубы теодолита будет фиксировать угол наклона ν, соответствующий проектному уклону. Затем, отметив на рейке или вехе высоту прибора, выполняют те же операции, что и при использовании нивелира. С меньшей точностью линию проектного уклона (например, точки А, В, С) можно вынести при помощи трех визирок одинаковой длины (рис. 90).
Рис. 90. Схема построения проектного уклона при помощи визирок
Две визирки задают опорную линию заданного уклона. В эту линию глазомерно вводят третью визирку, основание которой будет фиксировать точку линии проектного уклона. Для построения на местности проектной плоскости можно вынести в натуру точки А, В, С, D с известнымипроектными отметками (см. рис. 91). Действуя подъемными винтами нивелира, добиваются методом приближений, чтобы отсчеты на всех четырех точках были равны между собой, т. е. чтобы линия визирования была параллельна заданной проектной плоскости. При установке на тот же отсчет рейки в любой точке внутри фигуры ABCD пятка ее будет лежать в проектной плоскости.
Рис. 91. Схема построения проектной плоскости Можно от точки А построить линии АВ и АD с заданными проектными продольным и поперечным уклонами; затем от точки В линию ВС с известным поперечным уклоном. Назад
§ 66. ПЕРЕДАЧА ОТМЕТОК НА МОНТАЖНЫЕ ГОРИЗОНТЫ
Высотным разбивочным обоснованием на каждом монтажном горизонте служат рабочие реперы, отметки которых получены от исходных реперов высотной разбивочной основы. На монтажный горизонт переносят не менее двух реперов в зависимости от числа секций. Рабочими реперами могут служить закладные детали в конструкциях данного этажа или откраски на строительных конструкциях. Отметки на монтажный горизонт могут передаваться методом геометрического нивелирования с применением двух нивелиров и стальной компарированной рулетки. На исходном и монтажном горизонтах устанавливают нивелиры (рис. 92) (можно переносить один нивелир). На реперах, между которыми передаются отметки, устанавливают рейки. Берут отсчеты а и b по рейкам и отсчеты ℓ 2 и ℓ 1 по подвешенной рулетке. Разность отсчетов ℓ = ℓ 2 – ℓ 1 необходимо исправить поправками за компарирование и температуру. Искомую отметку монтажного горизонта Н монвычисляют по формуле
Н мон= Нисх + (а – b)+ ℓ, (66.1)
где Н исх – отметка репера на исходном горизонте. Точность передачи отметки этим способом будет зависеть в основном от ошибок отсчетов по рейкам и рулетке, компарирования реек и рулетки, учета температуры рулетки.
Рис. 92. Схема передачи отметки с исходного на монтажный горизонт
Передача отметки на монтажный горизонт может быть также выполнена путем фиксации отметки на строительных конструкциях исходного горизонта и вертикального линейного промера по строительным конструкциям до соответствующей откраски на монтажном горизонте. Для удобства пользования стараются на монтажном горизонте зафиксировать отметку, кратную целым метрам или полуметрам, например: +24,000 или +24,500. Для передачи отметки на дно котлована используется точно такой же способ как изложен выше. Следует только иметь ввиду, что отметка репера на дне котлована будет меньше чем отметка репера, расположенного на кромке котлована. Поэтому формулу (66.1) можно для этого случая переписать следующим образом:
Н мон = Н исх – (а – b) – ℓ. Назад
§ 67. СПОСОБЫ РАЗБИВКИ СООРУЖЕНИЙ Для выполнения разбивочных работ применяют следующие способы: полярных и прямоугольных координат, угловой, линейной и створной засечек. Способ угловой засечки применяют для разбивки недоступных точек, находящихся на значительном расстоянии от исходных пунктов. Различают прямую и обратную угловые засечки. В способе прямой угловой засечки положение на местности проектной точки С (рис.93) находят отложением на исходных пунктах А и В проектных углов β1 и β2. Базисом засечки служит или специально измеренная сторона, или сторона разбивочной сети. Проектные углы β1 и β2 вычисляют как разность дирекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам определяемой точки и известным координатам исходных пунктов.
На принципе редуцирования основано и применение для разбивки способа обратной угловой засечки. На местности находят приближенно положение О' разбиваемой проектной точки О (рис. 94). В этой точке устанавливают теодолит и с требуемой точностью измеряют углы не менее чем на три исходных пункта с известными координатами. По формулам обратной засечки вычисляют координаты приближенно определенной точки и сравнивают их с проектными значениями. По разности координат вычисляют величины редукций (угловой и линейный элементы) и смещают точку в проектное положение. Для контроля на этой точке измеряют углы, вновь вычисляют ее координаты и сравнивают их с проектными. В случае недопустимых расхождений все действия повторяют. В способе линейной засечки положение выносимой в натуру точки С (см. рис. 93) определяют в пересечении проектных расстояний S1и S2, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мерного прибора. Наиболее удобно разбивку производить при помощи двух рулеток. От точки А по рулетке откладывают расстояние S1, а от точки В по второй рулетке – S2. Перемещая обе рулетки при совмещенных нулях с центрами пунктов А и В, на пересечении концов отрезков S1и S2 находят положение определяемой точки С. Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены сравнительно недалеко от выносимых в натуру точек. В этом способе положение определяемой точки С (рис. 95) находят на местности путем отложения от направления АВ проектного угла β и расстояния S. Проектный угол β находится как разность дирекционных углов αАВ и αАС, вычисленных как и расстояние S из решения обратных задач по координатам точек А, В и С. Для контроля положение зафиксированной точки С можно проверить, измерив на пункте В угол β' и сравнив его со значением, полученным как разность дирекционных углов αВА и αВС'.
Способы створной и створно-линейной засечек широко применяют для выноса в натуру разбивочных осей зданий и сооружений, а также монтажных осей конструкций и технологического оборудования. Положение проектной точки С в способе створной засечки определяют на пересечении двух створов, задаваемых между исходными точками 1-1' и 2-2' (рис. 96). Створ задают обычно теодолитом, который центрируют над исходным пунктом (например, 1), а зрительную трубу ориентируют по визирной цели, отцентрированной на другом исходном пункте (в данном случае 1'). Положение точки С фиксируют в заданном створе. Средняя квадратическая погрешность створной засечки зависит от погрешностей построения первого и второго створов, а также погрешности фиксации опорных точек.
Рис. 96. Схема разбивки способами: а – створной засечки; б – створно-линейной засечки
Створно-линейный способ позволяет определить проектное положение выносимой в натуру точки С (см. рис. 96) путем отложения проектного расстояния d по створу АВ. Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано положение всех главных точек и осей проекта.
Назад
§68. ДЕТАЛЬНАЯ РАЗБИВКА ГОРИЗОНТАЛЬНЫХ КРИВЫХ
В ходе строительства автомобильных дорог часто используют наиболее простой способ выноса в натуру круговой либо клотоидной кривой от тангенциального хода, касательного к главным точкам трассы. В этом случае каждая элементарная кривая сложной трассы разбивается от своих тангенсов самостоятельно. Для этого случая предусмотрены три способа разбивки: 1. прямоугольных координат; 2. полярных координат; 3. углов и хорд. В зависимости от величины радиуса кривой при строительстве автомобильных дорог осуществляют детальную разбивку кривых с равным строительным шагом, принимаемым соответственно равным: 1, 2, 5, 10 или 20м. Способ прямоугольных координат. Если принять для круговой кривой тангенс за ось абсцисс, а направление от начала кривой или ее конца по нормали в сторону ее центра – за ось ординат (рис. 98, а), то детальную разбивку кривой со строительным шагом ℓ осуществляют в такой последовательности.
Центральный угол φ дуги ℓ определяется по формуле
Из треугольника 1R1' следует, что
y 1 = R – Rsin φ = 2R Учитывая, что разбивку кривой ведут с равным шагом ln, окончательно получим
φп = пφ; (68.2)
xn = Rsin φn; (68.3)
Рис. 98. Схема разбивки круговой кривой способом: а – прямоугольных координат; б – полярных координат; в – углов и хорд
Разбивку ведут с помощью теодолита (или эккера), ленты или рулетки. При этом ординаты у п откладывают по ленте, строят прямой угол с помощью теодолита (эккера) и сторожком обозначают соответствующую точку на местности. Способ полярных координат основан на том свойстве, что угол между осью абсцисс касательной в точке начала кривой и секущей, проведенной из начала координат на искомую точку, равен половине центрального угла, стягиваемого отсеченной дугой (рис. 98, б). Задавшись шагом разбивки lп по формуле (68.1), определяют половину центрального угла φ. Тогда величина угла δп для каждой точки составит:
Выполнив вычисления по формулам (68.2) – (68.4), устанавливают значения длин радиус-векторов для каждой точки кривой:
Разбивку кривой по методу полярных координат удобно осуществлять при использовании электронного тахеометра или оптического теодолита со светодальномерной насадкой, позволяющих измерять расстояния с высокой точностью. Для каждой точки откладывают горизонтальный угол δп и по лучу светодальномером расстояние Sn. Полученную точку обозначают на местности сторожком. Способ углов u хорд. В тех случаях, когда строительная организация не располагает электронными тахеометрами, либо светодальномерными насадками дляразбивки горизонтальных круговых кривых, может быть использован способ углов и хорд. Задавшись длиной хорды l,определяют угол φ /2 (рис. 98, в)
откуда
Теодолит устанавливают в точке О и ориентируют ноль лимба в направлении Х. Откладывая теодолитом угол φ /2 и лентой расстояние l получают точку 1, которую обозначают на местности сторожком. Откладывают угол 2(φ /2) и от точки 1расстояние l до пересечения с лучом теодолита, и получают точку 2 и т. д. Детальную разбивку клотоидных кривых при строительстве автомобильных дорог осуществляют, как правило, способами прямоугольных или полярных координат. Выбор того или иного способа диктуется местными условиями и наличием у строительной организации того или иного парка геодезических приборов. Детальную разбивку клотоидных кривых при строительстве автомобильных дорог, аналогично круговым, осуществляют с равным строительным шагом, соизмеряя его длину с параметром и длиной клотоиды. Отличие от разбивки круговых кривых заключается только в формулах, по которым вычисляются значения прямоугольных и полярных координат точек кривой. Назад § 69. СПОСОБЫ ПОДГОТОВКИ РАЗБИВОЧНЫХ ДАННЫХ Перед выносом в натуру проекта инженерного сооружения необходимо выполнить специальную геодезическую подготовку, которая предусматривает его аналитический расчет, геодезическую привязку проекта, составление разбивочных чертежей, разработку проекта производства геодезических работ. Для выноса сооружения в натуру необходимо иметь на местности геодезические пункты с известными координатами. В этой же системе должны быть получены координаты основных точек сооружения, определяющих его геометрию. Координаты пунктов геодезической разбивочной основы определяют по результатам измерений, проводимых при ее создании координаты точек, принадлежащих сооружению, определяют графически или вычисляют аналитически. При этом используют основные чертежи проекта: генеральный план, определяющий состав и местоположение сооружения; рабочие чертежи, на которых в крупных масштабах показаны планы, разрезы, профили всех частей сооружения с размерами и высотами деталей; план организации рельефа; планы и профили дорог, подземных коммуникаций. Весь комплекс геодезической подготовки проекта состоит из аналитического расчета элементов проекта. По значениям проектных размеров и углов находят в принятой системе проектные координаты основных точек сооружений, элементов планирования и благоустройства (осей проездов, коммуникаций, дорог и т.п.). Одновременно контролируют правильность нанесения размеров на чертежах. Различают три способа геодезической подготовки проекта: аналитический, графо-аналитический и графический. При аналитическом способе все данные для разбивки находят путем математических вычислений, причем координаты существующих зданий и сооружений определяют непосредственно геодезическими измерениями в натуре, а размеры элементов проекта задают, исходя из технологических расчетов. Этот способ применяют в основном при реконструкции и расширении предприятий, в стесненных условиях застройки. Чаще применяют графо-аналитический способ, когда положение исходных точек определяют графически с топографического плана, а остальных точек, жестко связанных с исходными,– аналитически. Например, для определения положения здания на местности по топографическому плану находят координаты одного из углов здания и дирекционное направление на другой угол. Далее по проектным размерам вычисляют координаты всех остальных углов здания.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 6516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.200.78 (0.017 с.) |

 Разбивочные работы являются одним из основных видов инженерно-геодезической деятельности. Выполняют их для определения на местности планового и высотного положений характерных точек и плоскостей строящегося сооружения в соответствии с рабочими чертежами проекта.
Разбивочные работы являются одним из основных видов инженерно-геодезической деятельности. Выполняют их для определения на местности планового и высотного положений характерных точек и плоскостей строящегося сооружения в соответствии с рабочими чертежами проекта. Разбивочные работы диаметрально противоположны съемочным. При съемке на основании натурных измерений определяют координаты точек относительно пунктов опорной сети. Точность этих измерений зависит от масштаба съемки. При разбивке, наоборот, по координатам, указанным в проекте, находят на местности положение точек сооружения с заранее заданной точностью. При разбивочных работах углы, расстояния и превышения не измеряют, а откладывают на местности. В этом основная особенность разбивочных работ.
Разбивочные работы диаметрально противоположны съемочным. При съемке на основании натурных измерений определяют координаты точек относительно пунктов опорной сети. Точность этих измерений зависит от масштаба съемки. При разбивке, наоборот, по координатам, указанным в проекте, находят на местности положение точек сооружения с заранее заданной точностью. При разбивочных работах углы, расстояния и превышения не измеряют, а откладывают на местности. В этом основная особенность разбивочных работ. В нормативных документах существует понятие разбивочной оси. На практике различают главные, основные, промежуточные, или детальные, оси.
В нормативных документах существует понятие разбивочной оси. На практике различают главные, основные, промежуточные, или детальные, оси.
 При построении проектного угла одна точка (вершина угла) и исходное направление обычно бывают заданы. Необходимо на местности отыскать второе направление, которое образовывало бы с исходным проектный угол β (рис. 85). В нашем случае ВА исходное направление, В – вершина проектируемого угла. Работы ведут в следующем порядке. Устанавливают теодолит в точку В. Наводят зрительную трубу на точку А и берут отсчет по лимбу. Далее прибавляют к этому отсчету проектный угол β и, открепив алидаду, устанавливают вычисленный отсчет. Теперь визирная ось зрительной трубы теодолита указывает второе искомое направление. Это направление на соответствующем проекту расстоянии фиксируют на местности в точке С 1.Аналогичные действия выполняют при другом круге теодолита и отмечают на местности вторую точку С 2. Из положения двух точек берут среднее (точку С), принимая угол АВС за проектный.
При построении проектного угла одна точка (вершина угла) и исходное направление обычно бывают заданы. Необходимо на местности отыскать второе направление, которое образовывало бы с исходным проектный угол β (рис. 85). В нашем случае ВА исходное направление, В – вершина проектируемого угла. Работы ведут в следующем порядке. Устанавливают теодолит в точку В. Наводят зрительную трубу на точку А и берут отсчет по лимбу. Далее прибавляют к этому отсчету проектный угол β и, открепив алидаду, устанавливают вычисленный отсчет. Теперь визирная ось зрительной трубы теодолита указывает второе искомое направление. Это направление на соответствующем проекту расстоянии фиксируют на местности в точке С 1.Аналогичные действия выполняют при другом круге теодолита и отмечают на местности вторую точку С 2. Из положения двух точек берут среднее (точку С), принимая угол АВС за проектный. ,
,








 На точность разбивки способом прямой угловой засечки оказывают влияние погрешности: собственно прямой засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки. Приразбивочных работах центрирование теодолита и визирных целей с помощью оптических отвесов, а также фиксация выносимой точки могут быть выполнены сравнительно точно. Поэтому основными погрешностями, определяющими точность способа прямой угловой засечки, являются погрешности собственно засечки и исходных данных. Суммарная величина этих погрешностей может составить значительных величин, что потребует выполнения угловой засечки с повышенной точностью.
На точность разбивки способом прямой угловой засечки оказывают влияние погрешности: собственно прямой засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки. Приразбивочных работах центрирование теодолита и визирных целей с помощью оптических отвесов, а также фиксация выносимой точки могут быть выполнены сравнительно точно. Поэтому основными погрешностями, определяющими точность способа прямой угловой засечки, являются погрешности собственно засечки и исходных данных. Суммарная величина этих погрешностей может составить значительных величин, что потребует выполнения угловой засечки с повышенной точностью. Требуемая точность разбивки в этом случае может быть достигнута следующим образом. Отложив с возможной точностью углы βl И β2, определяют в натуре положение точки С. Затем на опорных пунктах соответствующим числом приемов измеряют точное значение отложенных углов. Для приведенного примера при использовании теодолита 2Т30 надо выполнить не менее четырех приемов. Измеряют также угол γ на точке С. Распределив невязку в треугольнике поровну на все три угла, определяют координаты точки С. Сравнивая их с проектными значениями, находят поправки (редукции), по которым в натуре смещают (редуцируют) приближенно вынесенную точку С. Такой способ называют способом замкнутого треугольника.
Требуемая точность разбивки в этом случае может быть достигнута следующим образом. Отложив с возможной точностью углы βl И β2, определяют в натуре положение точки С. Затем на опорных пунктах соответствующим числом приемов измеряют точное значение отложенных углов. Для приведенного примера при использовании теодолита 2Т30 надо выполнить не менее четырех приемов. Измеряют также угол γ на точке С. Распределив невязку в треугольнике поровну на все три угла, определяют координаты точки С. Сравнивая их с проектными значениями, находят поправки (редукции), по которым в натуре смещают (редуцируют) приближенно вынесенную точку С. Такой способ называют способом замкнутого треугольника. Погрешность собственно разбивки полярным способом зависит от погрешности построения угла β и погрешности отложения проектного расстояния S. Расчет показывает, что для данных условий уменьшение погрешности в положении выносимой в натуру точки возможно лишь при существенном уменьшении погрешности отложения проектного расстояния – хотя бы в два раза.
Погрешность собственно разбивки полярным способом зависит от погрешности построения угла β и погрешности отложения проектного расстояния S. Расчет показывает, что для данных условий уменьшение погрешности в положении выносимой в натуру точки возможно лишь при существенном уменьшении погрешности отложения проектного расстояния – хотя бы в два раза.
 Если разбиваемая точка находится на значительном расстоянии от исходного пункта, то приходится несколько раз откладывать полярным способом проектные углы и расстояния, прокладывая проектный ход.
Если разбиваемая точка находится на значительном расстоянии от исходного пункта, то приходится несколько раз откладывать полярным способом проектные углы и расстояния, прокладывая проектный ход.

 Разбивку проектной точки С (рис. 97) производят по вычисленным значениям приращений ее координат Δ Х и Δ Y от ближайшего пункта сетки. Большее приращение (на рисунке Δ Y)откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпендикуляру откладывают меньшее приращение и закрепляют полученную точку С. Для контроля положение точки С можно определить от другого пункта строительной сетки. Схема способа прямоугольных координат, по существу, сочетает в себе схему створно-линейного и полярного способов.
Разбивку проектной точки С (рис. 97) производят по вычисленным значениям приращений ее координат Δ Х и Δ Y от ближайшего пункта сетки. Большее приращение (на рисунке Δ Y)откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпендикуляру откладывают меньшее приращение и закрепляют полученную точку С. Для контроля положение точки С можно определить от другого пункта строительной сетки. Схема способа прямоугольных координат, по существу, сочетает в себе схему створно-линейного и полярного способов. . (68.1)
. (68.1)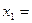 Rsin φ;
Rsin φ; .
. . (68.4)
. (68.4)
 .
. .
. ,
, .
. Если проект сооружения не связан с существующими строениями, то иногда применяют графический способ проектирования, при котором все планировочные элементы определяются графически по топографическому плану. Расчет проекта производят по графическим координатам всех его главных точек. Чтобы уменьшить влияние деформации планов, до определения графических координат измеряют действительные размеры квадратов координатной сетки. Для крупномасштабных планов они должны быть равны 100мм. При отклонении сторон квадрата на величину, не превышающую 0,2мм, координаты определяют следующим образом. через определяемую точку i проводят прямые, параллельные осям координат. Измеряют расстояния о и b соответственно от южной и северной сторон квад
Если проект сооружения не связан с существующими строениями, то иногда применяют графический способ проектирования, при котором все планировочные элементы определяются графически по топографическому плану. Расчет проекта производят по графическим координатам всех его главных точек. Чтобы уменьшить влияние деформации планов, до определения графических координат измеряют действительные размеры квадратов координатной сетки. Для крупномасштабных планов они должны быть равны 100мм. При отклонении сторон квадрата на величину, не превышающую 0,2мм, координаты определяют следующим образом. через определяемую точку i проводят прямые, параллельные осям координат. Измеряют расстояния о и b соответственно от южной и северной сторон квад 


