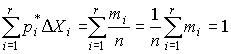Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По способу выражения результатов измерений различают абсолютные и относительные измерения.Содержание книги
Поиск на нашем сайте ТЕМА 2. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ) Основными единицами (их семь) являются следующие: длина – метр, масса – килограмм, время – секунда, сила электрического тока – ампер, термодинамическая температура – кельвин, сила света – кандела, количество вещества – моль. Основные единицы СИ с указанием сокращенных обозначений русскими и латинскими буквами приведены в табл. 1. Таблица 1
Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие. Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды. Килограмм равен массе международного прототипа килограмма. Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную Кельвин равен 1/273.16 части термодинамической температуры тройной точки воды. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой Дополнительные единицы СИ Международная система единиц включает в себя две дополнительныеединицы - для измерения плоского и телесного углов. Единица плоского угла - радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57°17'48". Стерадиан (ср), принимаемый за единицу телесного угла, - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы. Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. Единицы СИ Производные единицы Международной системы единиц образуются с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице. Так, для линейной скорости в качестве определяющего уравнения можно воспользоваться выражением для скорости равномерного прямолинейного движения: v = l / t. Единицы ФВ делятся на системные и внесистемные. Системная единица – единица ФВ, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными. Внесистемная единица – это единица ФВ, не входящая ни в одну из принятых систем единиц. Внесистемные единицы по отношению к единицам СИ разделяют на четыре вида: • допускаемые наравне с единицами СИ, например: единицы массы – тонна; плоского угла – градус, минута, секунда; объема – литр и др. • допускаемые к применению в специальных областях, например: астрономическая единица – парсек, световой год – единицы длины в астрономии; диоптрия – единица оптической силы в оптике; электрон-вольт – единица энергии в физике и т.д.; • временно допускаемые к применению наравне с единицами СИ, например: морская миля – в морской навигации; карат – единица массы в ювелирном деле и др.; • изъятые из употребления, например: миллиметр ртутного столба – единица давления; лошадиная сила – единица мощности и некоторые другие. Различают кратные и дольные единицы ФВ. Кратная единица – это единица ФВ, в целое число раз превышающая системную или внесистемную единицу. Например, единица длины километр равна 103 м, т. е. кратна метру. Дольная единица –единица ФВ, значение которой в целое число раз меньше системной или внесистемной единицы. Например, единица длины миллиметр равна 10-3 м, т. е. является дольной. Приставки для образования кратных и дольных единиц приведены в табл.. Таблица
Тема: Погрешности измерений Погрешностью измерения называют отклонение результата измерения от истинного значения измеряемой величины. Истинные значения физических величин – это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Результаты измерений представляют собой приближенные оценки значений величин, найденные путем измерения. Они зависят от метода измерения, от технических средств, с помощью которых проводятся измерения, и от свойств органов чувств наблюдателя, осуществляющего измерения. Поскольку истинное значение измеряемой величины неизвестно, то вместо истинного значения подставлять так называемое действительное значение. Под действительным значением физической величины понимают ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него (принимают обычно показания эталонов). Погрешности измерений классифицируются: по форме числового выражения, по источникам возникновения, по характеру проявлений. По форме числового выражения погрешности измерений подразделяют на абсолютные и относительные. В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения. Абсолютная погрешность определяется как разность ∆ = х - хд или ∆ = х-хд, а относительная – как отношение:
Приведенная погрешность В качестве истинного значения при многократных измерениях параметра выступает среднее арифметическое хи значение:
Средняя арифметическая полученная в одной серии измерений, является случайным приближением к хи. Для оценки ее возможных отклонений от хи определяют опытное среднее квадратическое отклонение (СКО):
Среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д. По источникам возникновения погрешности подразделяют на инструментальные (обусловлены свойствами средств измерений). методические (возникают вследствие несовершенства принятого метода измерений, допущений и упрощений при использовании эмпирических зависимостей) и субъективные (погрешности оператора). По характеру проявлений погрешности измерений подразделяют на систематические и случайные. Систематические погрешности остается постоянными или изменяются по определенному закону при повторных измерениях одной и той же величины. По характеру изменения во времени систематические погрешности подразделяют на постоянные и временные. Случайные погрешности (в том числе грубые погрешности и промахи) изменяются случайным образом при повторных измерениях одной и той же величины. Грубые погрешности – внезапное падение напряжения в сети электропитания. Промахи – погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов. В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы случайной и систематической погрешности.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность. Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами. Факторы, определяющие возникновение случайных погрешностей, проявляются нерегулярно, в различных комбинациях и с интенсивностью, которую трудно предвидеть. Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения. Интегральной функцией распределения называют функцию, значение которой для каждого x является вероятностью появления значений Xi (в i -м наблюдении), меньших x. График интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности. На рис. показаны примеры функций распределения вероятности.
Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей. Свойство плотности распределения вероятности: – вероятность достоверного события равна 1; Однако для наибольшего числа встречающихся на практике случайных величин можно ожидать распределение по так называемому закону нормального распределения (закону Гаусса). На рис. изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения
Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений. В производственной практике часто считается необходимым выполнения следующего условия: допустимое предельное отклонение от заданного номинального размера должно быть не меньше интервала ±3σ. В этом случае в среднем одно из 370 изделий будет бракованным. Обработка результатов измерений содержащих случайные погрешности. При большом числе результатов наблюдений (n >40) данная задача решается в следующем порядке. Весь диапазон полученных результатов наблюдений X max... X min разделяют на r интервалов (см. табл. далее) шириной ∆Xi (i = 1, 2, …, r) и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i -м интервале, т. е. меньших или равных его правой и больших левой границы. Отношения Pi, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i -й интервал:
Распределение частот по интервалам образует статистическое распределение результатов наблюдений. Отложим вдоль оси результатов наблюдений (рис.) интервалы ∆Xi в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной
Площадь суммы всех прямоугольников равна единице:
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, – к графику плотности распределения результатов наблюдений. При построении гистограмм рекомендуется пользоваться следующими правилами: 1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл..
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы. 3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.
Виды средств измерений. Меры – это средство измерений, воспроизводящие или хранящие физическую величину заданного размера. Измерительные преобразователи – СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не доступной для непосредственного восприятия наблюдателем (термопары, трансформаторы, усилители). Измерительный прибор – СИ, предназначенное для переработки сигнала измерительной информации в другие, доступные для непосредственного восприятия наблюдателем (амперметр, вольтметр, манометр). Измерительная установка – совокупность функционально объединенных СИ и вспомогательных устройств, расположенных в одном месте (поверочные установки). Измерительная система – это комплекс СИ и вспомогательных устройств с компонентами связи, предназначенные для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и использования в автоматических системах управления. В отличии от измерительных установок, предусматривающих изменения режима и условий функционирования, измерительная система не воздействует на режимы работы, а предназначена только для сбора и хранения информации. Система эталонов единиц ФВ Единство измерений достигается точным воспроизведением, хранением установленных единиц ФВ и передачей их размеров всем рабочим средствам измерений (РСИ) с помощью эталонов и образцовых средств измерений. Высшим звеном в метрологической цепи передачи размеров единиц измерений являются эталоны. Создание, хранение и применение эталонов, контроль за их состоянием подчиняются единым правилам, установленным ГОСТ “ГСИ. Эталоны единиц физических величин. Основные положения” и ГОСТ “ГСИ. Эталоны единиц физических величин. Порядок разработки, утверждения, регистрации, хранения и применения”. Эталон единицы – средство измерений (или комплекс средств измерений), обеспечивающее воспроизведение и хранение единицы с целью передачи ее размера нижестоящим по поверочной схеме средствам измерений, выполненное по особой спецификации и официально утвержденное в установленном порядке в качестве эталона. Конструкция эталона, его физические свойства и способ воспроизведения единицы определяются ФВ, единица которой воспроизводится, и уровнем развития измерительной техники в данной области измерений. Эталон должен обладать, по крайней мере, тремя взаимосвязанными свойствами: неизменностью, воспроизводимостью и сличаемостью. Неизменность – свойство эталона удерживать неизменным размер воспроизводимой им единицы в течение длительного интервала времени. Воспроизводимость –возможность воспроизведения единицы ФВ с наименьшей погрешностью для существующего уровня развития измерительной техники. Это достигается путем постоянного исследования эталона в целях определения систематических погрешностей и их исключения путем введения соответствующих поправок. Сличаемость – возможность сличения с эталоном других СИ, нижестоящих по поверочной схеме, в первую очередь вторичных эталонов, с наивысшей точностью для существующей техники измерения. Это свойство предполагает, что эталоны по своему устройству и действию не вносят каких-либо искажений в результаты сличений и сами не претерпевают изменений в результате сличений. Различают следующие виды эталонов (РМГ 29 – 99): • первичный – обеспечивает хранение и воспроизведение с наивысшей в стране (по сравнению с другими эталонами) точностью. Первичные эталоны – это уникальные СИ, часто представляющие собой сложнейшие измерительные комплексы, созданныe с учетом новейших достижений науки и техники. Они составляют основу государственной системы обеспечения единства измерений; • международный – эталон, принятый по международному соглашению в качестве международной основы для согласования с ним размеров единиц, воспроизводимых и хранимых национальными эталонами; • государственный или национальный –это первичный или специальный эталон, официально утвержденный в качестве исходного для страны. Государственные эталоны создаются, хранятся и применяются центральными метрологическими научными институтами страны. Государственные эталоны подлежат периодическим сличениям с государственными эталонами других стран. Термин "национальный эталон" применяется в случаях проведения сличения эталонов, принадлежащих отдельным государствам, с международным эталоном или при проведении так называемых круговых сличений эталонов ряда стран. • вторичный – хранит размер единицы, полученной путем сличения с первичным эталоном соответствующей ФВ. Вторичные эталоны являются частью подчиненных средств хранения единиц и передачи их размеров, создаются и утверждаются в тех случаях, когда это необходимо для организации поверочных работ, а также для обеспечения сохранности и наименьшего износа государственного эталона. Вторичные эталоны это эталоны-копии – предназначены для передачи размера единицы paбочим эталонам; эталоны сравнения – для взаимного сличения эталонов, которые не удается сличить непосредственно; рабочие эталоны – применяются для передачи размера единицы рабочим средствам измерений.
Вторичный или рабочий эталон, являющийся исходным для министерства (ведомства), иногда называют ведомственным эталоном. Совокупность государственных первичных или вторичных эталонов, являющихся основой обеспечения единства измерений в стране, составляет эталонную базу страны; Государственные эталоны создает, утверждает, хранит и применяет Государственный комитет по стандартам, вторичные – министерства и ведомства. Способы выражения погрешности эталонов устанавливает ГОСТ 8.381—80. Погрешности государственных первичных и специальных эталонов характеризуются неисключенной систематической погрешностью и нестабильностью. Неисключенная систематическая погрешность описывается границами, в которых она находится. Случайная погрешность определяется средним квадратическим отклонением (СКО) результата измерений при воспроизведении единицы с указанием числа независимых измерений. Нестабильность эталона задается изменением размера единицы, воспроизводимой или хранимой эталоном, за определенный промежуток времени. Оценки погрешностей вторичных эталонов характеризуются отклонением размеров хранимых ими единиц от размера единицы, воспроизводимой первичным эталоном. Для вторичного эталона указывается суммарная погрешность, включающая случайные погрешности сличаемых эталонов и погрешности передачи размеров единицы от первичного (или более точного) эталона, а также нестабильность самого вторичного эталона. Суммарная погрешность вторичного эталона характеризуется либо СКО результата измерений при его сличении с первичным эталоном или вышестоящим по поверочной схеме вторичным эталоном, либо доверительной границей погрешности с доверительной вероятностью 0,99. Передача размеров единиц ФВ от эталонов рабочим мерам и измерительным приборам осуществляется с помощью рабочих эталонов. До недавнего времени в нашей стране вместо термина "рабочие эталоны" использовался термин "образцовые средства измерений'*, который в большинстве других стран не применяется. Рабочие эталоны при необходимости подразделяются на разряды 1,2 и т.д., определяющие порядок их соподчинения в соответствии с поверочной схемой. Для различных видов измерений устанавливается, исходя из требований практики, различное число разрядов рабочих эталонов, определяемых стандартами на поверочные схемы для данного вида измерений.
Для ряда областей измерений, и в первую очередь для физико-химических измерений применяют стандартные образцы (СО). Стандартный образец – образец вещества (материала) с установленными в результате метрологической аттестации значениями одной или более величин, характеризующими свойство или состав этого вещества (материала). В зависимости от сферы действия и области применения определяется уровень утверждения стандартных образцов. По этому признаку они делятся на государственные, отраслевые и стандартные образцы предприятий. Тем СО, которые включены в поверочные схемы, присваивают разряды. Стандартные образцы объединяются в типы. Тип –это классификационная группировка образцов, определяющими признаками которых являются одно и то же вещество, из которого они изготовлены, и единая документация, по которой они выполнены. Типы СО допускаются к применению при условии их утверждения и регистрации в соответствующем реестре. Для каждого типа СО при их аттестации устанавливается срок действия (не более 10 лет) и определяются метрологические характеристики, которые нормируются в документации на их разработку и выпуск.
По способу выражения результатов измерений различают абсолютные и относительные измерения. Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант. Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате. Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную. В качестве примера относительных измерений можно привести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м3 воздуха к количеству водяных паров, которое насыщает 1 м3 воздуха при данной температуре. ОСНОВНЫЕ ХАРАКТЕРИСТИКАМИ ИЗМЕРЕНИЙ: 1. принцип измерений 2. метод измерений 3. погрешность 4. точность 5. правильность 6. достоверность Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта. Погрешность измерений - это отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Погрешность вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а так же недостаточным опытом наблюдателя или особенностями его органов чувств. Точность измерений - это характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины. Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит от того, насколько действительный размер единицы, в которой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений. Достоверность характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации. Наличие погрешности ограничивает достоверность измерений. Метод измерений - совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства. В соответствии с рекомендации по межгосударственной стандартизации различают: 1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы – на весах, силы электрического тока – амперметром. 2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента. 3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению. 4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.
5. Метод замещения — метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

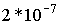 Н.
Н. Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

 , где xn –нормированное значение величины. Например, xn = xmax, где хmах – максимальное значение измеряемой величины.
, где xn –нормированное значение величины. Например, xn = xmax, где хmах – максимальное значение измеряемой величины. .
. .
.
 .
.

 . Полученный график называется гистограммой статистического распределения.
. Полученный график называется гистограммой статистического распределения.