
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерения. Запись и обработка результатов. Оценка погрешностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ИЗМЕРЕНИЯ. ЗАПИСЬ И ОБРАБОТКА РЕЗУЛЬТАТОВ. ОЦЕНКА ПОГРЕШНОСТЕЙ В основе точных естественных наук, к числу которых относится и физика, лежат измерения. При измерениях значения физических величин выражаются в виде чисел, которые указывают, во сколько раз измеренная величина больше или меньше другой величины, значение которой принято за единицу. Полученные в результате измерений числовые значения различных величии, например, времени, пути, скорости и т. д., могут зависеть друг от друга. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других. Получение надежных числовых значений физических величин отнюдь не является простой задачей из-за многочисленных погрешностей, неизбежно возникающих при измерениях. Ниже мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов, полученных при измерениях. Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наиболее близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точность полученных значений. Измерения и их погрешности Измерения делятся на прямые и косвенные. Прямые измерения производятся с помощью приборов, которые измеряют саму исследуемую величину. Так, массу тел можно найти с помощью весов, длину – измерить линейкой, а время – секундомером. Те же величины в других случаях могут быть найдены только с помощью косвенных измерений – путем пересчета других величин. Так находится масса Земли, расстояние от Земли до Солнца, продолжительность геологических периодов. Измерения плотности тел по их массе и объему, скорости поезда – по величине пути, пройденного за известное время, также принадлежат к косвенным измерениям. Качество измерений определяется их точностью. При прямых измерениях точность опытов устанавливается из анализа точности метода и приборов, а также из повторяемости результатов измерений. Точность косвенных измерений зависит как от надежности используемых для расчета данных, так и от структуры формул, связывающих эти данные с искомой величиной. Точность измерений характеризуется их погрешностью. Погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая погрешность измерения величины x символом Δ х, найдем Δ х = xизм – xист. (1) Кроме абсолютной погрешности Δ х, часто бывает важно знать относительную погрешность δ х, которая равна отношению абсолютной погрешности к значению измеряемой величины: Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении длины стола может уже быть существенна, а при определении диаметра болта совершенно недопустима. Это происходит потому, что относительная погрешность измерений в первом случае составляет ~2·10–4, во втором ~10–3, а в третьем может составлять десятки процентов и более. Вместо того, чтобы говорить об абсолютной и относительной погрешности измерений, часто говорят об их абсолютной и относительной ошибке. Между терминами «погрешность» и «ошибка» нет никакого различия, и мы будем пользоваться ими обоими. Как следует из (1) и (2), для того, чтобы найти абсолютную и относительную погрешность измерений, нужно знать не только измеренное, но и истинное значение интересующей нас величины. Но если истинное значение известно, то незачем производить измерения. Цель измерений всегда состоит в том, чтобы узнать не известное заранее значение физической величины и найти если не ее истинное значение, то хотя бы значение, достаточно мало от него отличающееся. Поэтому формулы (1) и (2), определяющие величину погрешностей, для практики непригодны. При практических измерениях погрешности не вычисляются, а оцениваются. При оценках (которые редко удается провести с точностью лучше 20–30%) учитываются условия проведения эксперимента, точность методики, качество приборов и ряд других факторов. Цель нашего Введения заключается в том, чтобы научить студентов разумно строить методику эксперимента, правильно использовать полученные на опыте данные для того, чтобы находить достаточно близкие к истинным значения физических величин и разумно оценивать погрешности измерений. Случайные погрешности Случайные величины, к которым относятся случайные погрешности, изучаются в теории вероятностей и в математической статистике. Мы здесь опишем – с пояснениями, но без доказательств – основные свойства и основные правила обращения с такими величинами в том объеме, который необходим для обработки результатов измерений, полученных в лаборатории. В этом параграфе мы будем предполагать, что систематические погрешности пренебрежимо малы и все ошибки сводятся к случайным. Позднее, в § 5, мы обсудим, как следует поступать в тех случаях, когда нужно принимать во внимание как случайные, так и систематические погрешности опыта. Рассмотрим для примера данные, полученные при измерении массы тела на весах, у которых имеется область застоя из-за трения призмы на подушке (разброс результатов для наглядности преувеличен). Пусть масса тела близка к 48 мг, результат измерений удается отсчитать по шкале с точностью до 0,1 мг. Имеем:
Вместо одного нужного нам результата мы получили одиннадцать. Что делать с полученными цифрами? Как найти из них достаточно близкое к истинному значение массы тела и как оценить погрешность полученного результата? Этот вопрос подробно изучается в математической статистике. Мы здесь изложим соответствующие правила без вывода. В качестве наилучшего значения для измеренной величины обычно принимают среднее арифметическое из всех полученных результатов:
В нашем случае получим mср = Этому результату следует приписать погрешность, определяемую формулой
В нашем случае
Результат опыта записывается в виде х = xср ± σx. (5) В нашем случае m = (48,10± 0,10)мг. Рассмотрим формулы (3) и (4). Прежде всего, попытаемся понять, как зависит результат расчета от числа измерений. Формула (3) показывает, что xср от числа измерений зависит слабо. Все слагаемые, входящие в числитель, приблизительно равны друг другу. Их сумма пропорциональна числу слагаемых. После деления на знаменатель получается величина, мало зависящая от числа измерений. Так, конечно, и должно быть. Среднее измеренное значение – при правильной методике опыта – всегда лежит вблизи истинного значения и в разных независимых сериях измерений испытывает вокруг него небольшие случайные колебания. Погрешность опыта, определяемая формулой (4), с увеличением числа измерений п уменьшается как
(Число членов суммы в (4) растет как п, числитель (4) поэтому увеличивается как Формула (4) может быть записана в несколько ином виде
При такой записи множитель 1/
При обсуждении смысла величины σ следует помнить, что истинную величину погрешности невозможно узнать до тех пор, пока из каких-либо других опытов (или соображений) не удастся определить искомую величину с существенно лучшей точностью. Но тогда рассматриваемые опыты потеряют значение, и их погрешность никого не будет интересовать. Как уже отмечалось, погрешность результата не столько определяют, сколько оценивают. Оценка (4) подобрана так, что при проведении многочисленных серий измерений погрешность в 2/3 случаев оказывается меньше σ x, а в 1/3 случаев больше, чем σ x. Иначе говоря, если бы мы – в нашем случае – провели не одну серию из 11 взвешиваний, а десять таких серий, то мы могли бы ожидать, что в шести или семи из них усредненный результат будет отличаться от истинной массы тела меньше чем. на 0,1 мг. а в остальных случаях больше, чем, на 0,1 мг. Погрешность, определенную с достоверностью 2/3, обычно называют стандартной (или среднеквадратичной) погрешностью опытов, а ее квадрат – дисперсией. Можно показать, что, как правило, погрешность опыта только в 5% случаев превосходит ±2σ и почти всегда оказывается меньше ±3σ. На первый взгляд из сказанного можно сделать вывод, что, беспредельно увеличивая число измерений, можно даже с самой примитивной аппаратурой получить очень хорошие результаты. Это, конечно, не так. С увеличением числа измерений уменьшается только случайная погрешность опытов. Методические погрешности и погрешности, связанные с несовершенством приборов (например, с неправильностью их шкалы), при увеличении числа опытов не меняются. В приведенном выше примере результат взвешивания округлялся до десятых долей миллиграмма. Это-делалось потому, что сотых долей отсчитать было нельзя. Одна только ошибка отсчета составляет при этом около 0,1 мг. Поэтому погрешность результата ни при каком числе опытов не может быть сделана меньше. Число опытов в нашем случае было-выбрано разумно. Из приведенных в таблице цифр ясно, что при однократном измерении мы могли ошибиться на несколько десятых. Среди цифр встречаются результаты, отличающиеся на 0,3 и даже на 0,5 от среднего. После усреднения по 11 измерениям погрешность существенно уменьшилась. Но если окажется нужным узнать массу тела с лучшей, чем это мы сделали, точностью, то недостаточно просто увеличить число измерений. Придется взять более точные весы, позволяющие производить измерения не до десятых, а, скажем, до сотых долей миллиграмма. Скажем несколько слов о формуле (4). Эта формула позволяет хорошо оценивать величину стандартной погрешности в тех случаях, когда число опытов оказывается не меньше 4–5. При меньшем числе опытов лучше применять другие, более сложные оценки. Их мы, однако, рассматривать не будем, во-первых, чтобы не удлинять и не усложнять текста, а, во-вторых, по той причине, что надежность всех этих оценок при малом числе измерений оказывается невысокой. Систематические погрешности Оценку систематических погрешностей экспериментатор производит, анализируя особенности методики, паспортную точность приборов и производя контрольные опыты. Систематические погрешности электроизмерительных приборов, выпускаемых промышленностью (амперметров, вольтметров, мостов, потенциометров и т. д.), определяются их классом точности, который обычно выражают в процентах. Амперметр класса 0,2 (если он, конечно, исправен и проходит систематическую проверку) позволяет производить измерения с абсолютной погрешностью, не превосходящей 0,2% от тока, соответствующего полной шкале прибора. На всех участках шкалы – в ее начале, середине и конце – эта погрешность одна и та же. Отметим различие в правилах определения погрешностей и в определении класса точности. Погрешности принято характеризовать среднеквадратичными ошибками. При многочисленных измерениях реальная ошибка опытов только в 2/3 случаев меньше среднеквадратичной, а в 1/3 случаев превосходит ее. Класс точности определяет максимально возможное значение погрешности. Приборы, которые могут давать – хотя бы иногда – бóльшие погрешности, должны быть отнесены к другому классу. Такое различие в определениях очень неудобно. В научных публикациях принято приводить именно среднеквадратичную ошибку, а вовсе не максимальную. Строгих формул для перевода одних погрешностей в другие не существует. Можно пользоваться следующим простым правилом: чтобы оценить среднеквадратичную погрешность измерений электроизмерительными приборами, следует погрешность, определяемую классом.точности прибора, разделить на два. Как уже отмечалось, класс электроизмерительных приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, поэтому приборы обеспечивают хорошую точность при отклонении стрелки почти на всю шкалу и не дают ее при измерениях в начале шкалы. Отсюда следует рекомендация: выбирать прибор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы. Говоря о систематических погрешностях опыта, следует сказать несколько слов об ошибке отсчета «на глаз». Большинство приборов не имеет нониуспых шкал. При этом доли деления отсчитываются на глаз. Эта ошибка составляет 1–2 десятых доли деления. При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для облегчения установки глаза на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора установлен правильно, если стрелка прибора закрывает свое изображение в зеркале. При работе с электроизмерительными приборами отсчет должен включать число целых делений и число десятых долей деления, если отсчет может быть произведен с этой точностью (если стрелка или зайчик не ходят и не дрожат, что может сделать аккуратный отсчет невозможным). Поясним указанное правило. Шкалы электроизмерительных приборов обычно изготовляют так, что одно деление шкалы приблизительно равно максимальной погрешности прибора. Зачем же в этом случае отсчитывать десятые доли деления? Ответ на этот вопрос читатель найдет в § 7. Забегая вперед, отметим, что при измерениях, при расчетах и при записи результатов, кроме надежно известных значащих цифр, всегда указывается одна, лишняя. Такая процедура, среди прочих, имеет и то преимущество, что позволяет вовремя замечать мелкие нерегулярности исследуемых зависимостей. Если, например, стрелка прибора при измерениях отклонилась на полделения назад, этот результат является надежным и в том случае, когда погрешность прибора равна целому делению. Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ±0,05 мм, а сантиметровые – не хуже, чем с точностью 0,1 мм. Погрешность измерений, производимых с помощью таких линеек, практически равна погрешности отсчета на глаз. Деревянными или пластиковыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0,01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точностью нониуса (у штангенциркулей цена делений нониуса составляет обычно 0,1 или 0,05 мм). Пример графической обработки экспериментальных данных Поясним изложенное с помощью простого примера.
V=a+bI. Чтобы найти параметры этой прямой, заметим, что ее продолжение.пересекает ось ординат при напряжении 2,1 В. Ток 150 мА достигается при напряжении 10,9 В. Поэтому a = 2,1 В, b = (10,9-2,1)/0,150 = 58,7 В/А. Найдем погрешность указанных значений. В соответствии-с правилом, указанным в тексте, следующем за формулой (20), проведем на рис. 7 две прямые, параллельные основной прямой и обладающие тем свойством, что по одну сторону каждой из них лежит вдвое больше экспериментальных точек, чем по другую,– эти прямые на рис. 7 проведены пунктиром. Расстояние между прямыми Δ а = 0,3 В. Полное число точек на графике составляет 29. По формуле (21) найдем, что погрешность в определении а равна σa = Δ а / К этой погрешности нужно прибавить ошибку отсчета на миллиметровой бумаге (0,5 мм, т. е. 0,05 В) и ошибку, связанную с погрешностью вольтметра. Последняя равна половине погрешности, соответствующей классу точности вольтметра, т. е. σa, сист = ½ · 2%·15= 0,15 В. Полная погрешность равна σa, полн = При расчете погрешности можно было сразу заметить, что одна из погрешностей, а именно σa, сист, много больше других, и принимать во внимание ее одну. При нашей точности 0,15 и 0,17 не отличаются друг от друга. Скажем несколько слов об ошибке, вносимой в результат погрешностями миллиамперметра. В нашем случав эту погрешность можно не учитывать, потому что измерения проводились с помощью прибора, имеющего высокий класс точности. Если это было бы не так, то токовую погрешность, вносимую миллиамперметром (в нашем случае (1/2)·0,5%·0,15 А = 3,7 · 10–4 А), нужно было бы с помощью параметра b пересчитать в погрешность напряжения (в нашем случае 3,7·10–4·58,7·10–2 В=2,2·10–4 В), возвести в квадрат и внести в подкоренное выражение, служащее для вычисления σa, полн, в качестве одного из слагаемых. Найдем погрешность в определении параметра b. На рис. 8 проведены две прямые в соответствии с рекомендациями, приведенными в тексте, который предшествует формуле (22). С помощью рис. 8 найдем Δ b =b 1 – b 2= 8,2 В/А. Погрешность в определении b согласно (22) равна σb = Δ b / Систематическую часть погрешности оценим, исходя из класса точности вольтметра. Полагая для оценки, что вся ошибка сосредоточена на одном краю шкалы, и учитывая правило, согласно которому погрешность, определяемую классом точности, при расчете ожидаемых ошибок нужно уменьшить вдвое, получим σb, сист = Погрешность отсчета по миллиметровой бумаге вносит в ошибку вклад
Полная погрешность в определении b равна σb, полн = Имеем окончательно а = 2,1 ± 0,2 В, b = 58,7 ± 1,8 В/А. При написании этих значений мы следовали правилу, согласно которому найденное число и его погрешность должны записываться до одного и того же разряда, в нашем случае – включая первый знак после запятой. При написании численного значения а мы округлили погрешность до 0,2 В в соответствии c правилом, сформулированным в § 7. Посмотрим еще раз на расположение экспериментальных точек на графиках рис. 7 и 8. Эти точки нередко отклоняются от проведенной прямой на 0,2–0,3 В. Хотя такие отклонения не противоречат точности вольтметра, разброс точек явно связан не с ним. В самом деле, экспериментальные точки разбросаны вокруг прямой без всякого порядка. Невозможно предположить, что погрешности прибора ведут себя таким образом: ни сила магнита, ни упругость волоска, ни расположение делений на шкале так беспорядочно «прыгать» не могут. К разбросу точек привела какая-то другая причина, которая не была нами своевременно замечена. Возможно, что эти «прыжки» связаны с плохим качеством контактов,– их следовало бы закрепить или пропаять, а затем повторить опыт. Возможно, что источник питания недостаточно стабилен. Это нужно было бы выяснить и иметь в виду в будущем. Вероятнее же всего, что колебания результатов вызваны плохим контактом в переменном сопротивлении R. Результаты рис. 7 и 8 на самом деле нужно не пускать в обработку, а получить заново, устранив в схеме неисправность. (Мы их оставили здесь в качестве учебного примера.) Заметим, что этот важный вывод мы сделали, анализируя графики рис. 7 и 8. Без графиков к этому заключению прийти было бы намного труднее. Пример аналитической обработки экспериментальных данных Можно найти значения параметров а и b прямой, которая описывает результаты описанного в предыдущем разделе эксперимента, и не прибегая к графикам. Для расчета следует использовать формулы (24) и (27). Поясним ход расчета на примере. В приводимой здесь таблице представлены экспериментальные данные, по которым построены графики рис. 7 и 8:
С помощью калькулятора найдем (I ≡ х, V ≡ у): <х> = 7,9214·10–2 A, < у > = 6,7276 В, < xy > = 0,63236 В·А, <х 2 > = 7,9557 · 10–3 А2, <у 2 > = 51,2114 В2, D(х) = 1,6809 · 10–3 А2, D(у) = 5,9510 В2. По формулам (24) найдем
Найденные погрешности σb и σ a следует сложить с систематическими погрешностями так же, как это было сделано в предыдущем параграфе. Результаты расчета параметров b и а несколько отличаются от результатов, найденных графически, но различие между ними существенно меньше, чем погрешность опытов. Результаты расчета погрешностей отличаются несколько сильнее. Заметим, однако, что для нахождения параметров и их погрешностей, расчетным методом потребовалось много труда, так как вычисление средних значений и дисперсий занимает много времени и приходится производить с большим количеством значащих цифр. Сильное взаимное сокращение членов хорошо видно на примере вычисления σb, где промежуточные результаты выписаны в явном виде. Столь же сильное сокращение членов происходит при вычислении дисперсий х и у. К этому следует прибавить, что аналитический расчет параметров и их погрешностей обычно не избавляет от необходимости строить графики. В самом деле, только взгляд на график убедил нас в том, что вольтамперная характеристика нашего образца хорошо описывается линейной зависимостью. Изучение графика показало нам также, что в схеме имеется нестабильность, которую мы своевременно не заметили. К этим выводам можно прийти и без графика, анализируя табличные данные. Но графический метод позволяет это сделать намного быстрее и нагляднее. Заключение В заключение еще раз отметим, что паше изложение не претендует ни на полноту, ни на строгость. Оно содержит обзор правил и формул, которые нужно применять, чтобы грамотно обрабатывать полученные экспериментальные данные и приводить их к общепринятому, всем попятному виду. Более глубокое изложение потребуется – и станет возможным – лишь после первых двух курсов обучения, когда будет накоплен достаточный опыт экспериментальной работы и окажется развит необходимый для такого изложения математический аппарат. Поясним сказанное. Мы внимательно рассмотрели в предыдущих параграфах задачу о том, как провести через полученные экспериментальные точки наилучшую прямую и как найти погрешности, возникающие при определении ее параметров. А как проводить наилучшую гиперболу? Как найти параметры кривых, если результат опыта описывается суммой двух экспонент с разными коэффициентами и с различными – заранее не известными – показателями (к такой задаче часто приводит анализ радиоактивного распада), и т. д.? При расчете погрешностей мы рекомендовали пользоваться формулой (4) в том случае, если число измерений равно хотя бы четырем. Существует теория (распределение Стьюдента), которая позволяет получать оценки (не очень, впрочем, надежные) и при меньшем числе измерений. Мы не касались этого вопроса. Мы не рассмотрели и другую важную задачу. Прежде чем находить параметры наилучшей прямой (или другой какой-нибудь заданной зависимости), следует убедиться в том, что полученный набор экспериментальных значений действительно может быть описан прямолинейной зависимостью (или зависимостью другого наперед заданного вида), а не требует привлечения более сложных формул. В начале § 12 мы сказали, что взгляд на рис. 7 убеждает нас в том, что вольтамперная характеристика нашего образца – в рассмотренном диапазоне значений – может быть описана линейной зависимостью. Взгляд на рис. 7, действительно, в этом убеждает. Ну, а если кто-нибудь усомнится, то как его убедить? Поставленный вопрос, конечно, не может решаться в ту или другую сторону только с помощью интуиции. Необходимо иметь количественные критерии, позволяющие в спорных случаях проверять, наблюдается ли на самом деле более сложная зависимость или можно обойтись простой формулой. Мы задали здесь эти вопросы не для того, чтобы на них ответить, а с тем, чтобы несколько расширить кругозор студентов. Ответы на эти вопросы могут быть получены, но заниматься этим сейчас не время. Для этого необходимо накопить опыт лабораторной работы и приобрести простейшие навыки обработки экспериментальных результатов. Изложенный здесь материал для этого достаточен. Некоторые разъяснения читатель найдет в Приложении, помещенном в конце книги. Приступать к его изучению следует, однако, не ранее чем в начале второго года обучения. Сводка формул
ПРИЛОЖЕНИЕ Распределение Пуассона В физике часто приходится встречаться с измерениями, результаты которых представляются в виде целых чисел. Через счетчик Гейгера за время измерения приходит целое – и обычно не очень большое – число частиц. Делящееся ядро распадается на целое число частей. Статистические закономерности, которые имеют место в этом случае, обладают некоторыми особенностями. Рассмотрим счетчик, регистрирующий космические частицы. В то время как число отсчетов счетчика за любой промежуток времени является целым числом, интенсивность ν космического излучения (т. е. отнесенное к единице площади число отсчетов счетчика в секунду, усредненное за очень большой отрезок времени), вообще говоря, целым числом не выражается. Найдем вероятность того, что при интенсивности ν счетчик за время измерения сработает n раз. Будем для простоты считать, что счетчик обладает единичной площадью,– окончательные формулы от этого предположения не зависят. Поскольку мы приступаем к вычислению вероятностей, следует представить себе очень большое число совершенно одинаковых одновременно работающих счетчиков. Некоторая часть их сработает ровно n раз. Доля, составляемая этими счетчиками, по отношению к полному числу счетчиков и равна вероятности того, что через счетчик за время измерения пройдет n частиц. Обозначим полное число счетчиков буквой N. Через них в секунду в среднем проходит N ν частиц, а за небольшое время dt пройдет N ν dt частиц. Если dt достаточно мало, то ни через один из счетчиков за это время не пройдет двух частиц, и наши счетчики можно разбить на два класса: те, через которые за dt прошла частица, и те, через которые не прошла. Последние составляют, конечно, огромное большинство. Число счетчиков, через которые прошла частица, равно, очевидно, числу сосчитанных частиц, т. е. приблизительно N ν dt, а их доля по отношению к полному числу счетчиков составляет N ν dt / N= ν dt. Вероятность того, что за время dt через счетчик пройдет частица, равна, следовательно, ν dt. Это утверждение справедливо только в том случае, если dt очень мало. Вычислим теперь вероятность P 0(t) того, что за время t через счетчик не пройдет ни одной частицы. По определению число таких счетчиков в момент t составляет NP 0(t), а в момент t + dt равно NP 0(t + dt). Это число меньше, чем NP 0(t), потому что за время dt их число убавится на NP 0(t)ν dt. Поэтому NP 0(t + dt) = NP 0(t) – NP 0(t)ν dt, или P 0(t + dt) – P 0(t) = – P 0(t)ν dt, Деля это равенство на dt и переходя к пределу, получим: dP 0/ dt= –ν P 0 Интегрируя, найдем: P 0(t) = – e– ν t. (П.1) При интегрировании было принято во внимание, что в начальный момент времени вероятность найти счетчик, не сработавший ни разу, равна, конечно, единице. Вычислим теперь Pn (t + dt) – вероятность того, что за время: t + dt через счетчик пройдет ровно n частиц. Эти счетчики делятся на две группы. К первой принадлежат те, через которые все n частиц прошли за время t, а за время dt не прошло ни одной. Ко второй группе принадлежат счетчики, через которые за время t прошла n – 1 частица, а последняя частица прошла за время dt. Число первых счетчиков равно NPn (t)(1 – ν dt), а число вторых составляет NPn– 1(t)ν dt. (Каждое из этих выражений состоит из двух сомножителей. Первый из них определяет вероятность нужного числа срабатываний за время t, а второй – вероятность несрабатывания или срабатывания за время dt.) Имеем, следовательно: NPn (t + dt) = NPn (t)(1 – ν dt) – NPn– 1(t)ν dt. Перенесем NPn (t)(1 – ν dt) в левую часть равенства и разделит его на Ndt:
Последовательно применяя полученную рекуррентную формулу к n = 1, n = 2 и т. д., с помощью (П.1) найдем:
Заметим теперь, что ν t, которое мы обозначим через n 0, равно среднему числу частиц, проходящих через счетчик за время t. Наша формула примет вид
Эта формула является окончательной и носит название закона распределения Пуассона. Она определяет вероятность того, что при среднем числе срабатываний n 0 (это число, вообще говоря, не является целым) произойдет именно n срабатываний (n – целое число).
Для иллюстрации на рис. 1 изображено распределение Пуассона для n 0 = 2,6. Ни для какого n величина Pn не равна нулю. Она достигает максимума при n = 2. Вероятность найти n = 0 оказывается довольно велика. Достаточно велика также вероятность того, что счетчик срабатывает 3, 5 и даже 7 раз. Рассмотрим некоторые свойства формулы (П.2). Вычислим, прежде всего, вероятность найти какое угодно значение n:
Этот результат является очевидным, потому что хоть какое-нибудь значение n, конечно, всегда будет найдено на опыте, так что мы вычисляли вероятность достоверного события. Вычислим среднее значение n:
Полученный результат тоже можно было предсказать заранее, поскольку мы исходили из того, что среднее значение n равно n 0. Найдем теперь среднеквадратичное отклонение (стандартную ошибку) величины n. Для этого сначала вычислим дисперсию n (среднее значение квадрата отклонения):
Вычисление суммы в качестве полезного упражнения мы предоставляем читателям. Имеем, следовательно:
Этот результа
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.015 с.) |

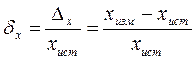 . (2)
. (2) . (3)
. (3) (48,0 + 47,9 +... + 48,1 + 48,2) = 48,1 мг.
(48,0 + 47,9 +... + 48,1 + 48,2) = 48,1 мг. (4)
(4)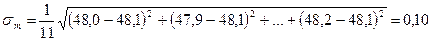 мг.
мг. :
: . (6)
. (6) .
. .
.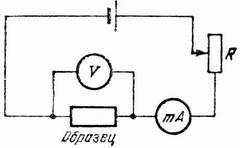 Пусть рис. 7 и 8 (они содержат один и тот же набор экспериментальных точек) изображают результаты исследования вольтамперной характеристики образца на установке, изображенной на рис. 9. Сила тока, проходящего через образец, измеряется миллиамперметром тА (полная шкала 150 мА, класс точности 0,5), а напряжение на нем – вольтметром V (полная шкала 15 В, класс точности 2). Сила тока регулируется резистором R. По оси абсцисс отложена сила тока в миллиамперах, а по оси ординат – напряжение в вольтах. Рассмотрев распределение точек на рисунках, мы видим, что экспериментальные данные в рассматриваемом диапазоне токов и напряжений (10 мА ≤ I ≤ 150 мА, 3 В≤ V ≤ 11 В) хорошо ложатся на прямую линию
Пусть рис. 7 и 8 (они содержат один и тот же набор экспериментальных точек) изображают результаты исследования вольтамперной характеристики образца на установке, изображенной на рис. 9. Сила тока, проходящего через образец, измеряется миллиамперметром тА (полная шкала 150 мА, класс точности 0,5), а напряжение на нем – вольтметром V (полная шкала 15 В, класс точности 2). Сила тока регулируется резистором R. По оси абсцисс отложена сила тока в миллиамперах, а по оси ординат – напряжение в вольтах. Рассмотрев распределение точек на рисунках, мы видим, что экспериментальные данные в рассматриваемом диапазоне токов и напряжений (10 мА ≤ I ≤ 150 мА, 3 В≤ V ≤ 11 В) хорошо ложатся на прямую линию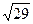 = 0,06 В.
= 0,06 В.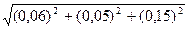 = 0,17 В.
= 0,17 В.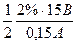 = 1,0 В/А.
= 1,0 В/А.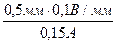 = 0,3 В/А.
= 0,3 В/А. = 1,8 В/A.
= 1,8 В/A.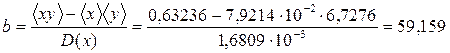 В/А,
В/А, В.
В.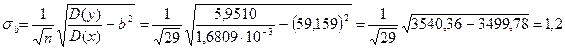 В/А,
В/А, В.
В.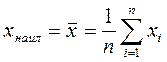
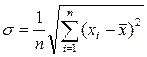 (формула справедлива при п ≥ 4 или 5)
(формула справедлива при п ≥ 4 или 5)
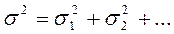
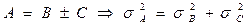
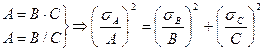
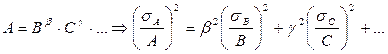
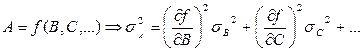
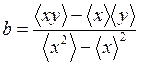 ,
, 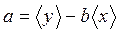
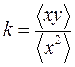

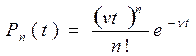 .
.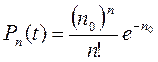 (П.2)
(П.2) Закон распределения Пуассона записан в такой форме, что из всех характеристик работы счетчика осталась только одна – его среднее число срабатываний за время измерения. Ни само время измерения, ни, тем более, площадь счетчика, которую мы вначале для простоты положили равной единице, в формулу не входят. Равным образом в формуле никак не отражено то обстоятельство, что мы рассматривали счетчик Гейгера, регистрирующий космическое излучение. С равным успехом эта формула применима к числу соединений на телефонной станции или к любой другой задаче, где число случаев является целым, а их появление в любой момент времени не зависит от числа случаев, произошедших ранее (независимые события).
Закон распределения Пуассона записан в такой форме, что из всех характеристик работы счетчика осталась только одна – его среднее число срабатываний за время измерения. Ни само время измерения, ни, тем более, площадь счетчика, которую мы вначале для простоты положили равной единице, в формулу не входят. Равным образом в формуле никак не отражено то обстоятельство, что мы рассматривали счетчик Гейгера, регистрирующий космическое излучение. С равным успехом эта формула применима к числу соединений на телефонной станции или к любой другой задаче, где число случаев является целым, а их появление в любой момент времени не зависит от числа случаев, произошедших ранее (независимые события). .
.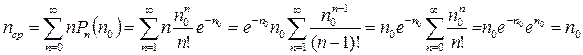 .
. .
.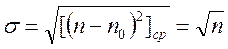 (П.3)
(П.3)


