
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение искомых параметров по результатам измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Очень часто цель экспериментов заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле. Так, на Земле падение тел описывается формулой S = gt 2 / 2, но величина g меняется от одного участка земной поверхности к другому и подлежит экспериментальному определению. Радиоактивный распад подчиняется формуле N=N0 e-λt, где N – количество атомов вещества в момент t, N0 – начальное число атомов, а λ – постоянная распада. Закон распада имеет один и тот же вид для всех ядер, но постоянная λ у каждого из них своя. Параметр λ определяется экспериментально. Растяжение тел описывается формулой
где L – длина образца, Δ L – его удлинение под действием силы F, S – площадь образца, Е – константа (модуль упругости). Написанная формула – при небольших силах – описывает растяжение всех твердых тел, но величина модуля упругости зависит от материала, его обработки и т. д. Эта величина находится экспериментально. Пусть опыт состоит в определении модуля упругости. Экспериментатор измеряет L и S и записывает формулу в виде
Затем тело растягивают и составляют таблицу зависимости удлинения от приложенной силы:
Как найти Е по данным, указанным в этой таблице? Можно попытаться записать цепь равенств:
Нередко приходится наблюдать, что при обработке результатов студенты усредняют найденные таким образом значения модуля упругости. Это плохой, математически некорректный метод. Поясним наше утверждение. На рис. 6 точками изображены результаты 11 опытов (разброс точек для наглядности увеличен). Первое из равенств соответствует прямой, проведенной из начала координат через точку 1. В самом деле, из этого равенства имеем Рис. 6 показывает, однако, что усредняемые величины определяются из опыта с разной достоверностью. Точка 8 отстоит от наилучшей прямой (которая проведена жирной линией) не ближе, чем точка 2, но погрешность в определении угла для нее в несколько раз меньше. Обсуждаемый способ определения Е заключается, таким образом, в том, чтобы взять среднее из хороших и плохих результатов. Такая процедура, конечно, математически некорректна. Иногда пытаются найти Е из прироста длины и силы на каждом шаге растяжения:
При этом возникает много вычислительной работы и получается новый ряд значений Е, которые также чаще всего усредняют. Покажем, что и этот способ неправилен. Пусть, для примера, опыт ставится в условиях, когда все приращения длины равны друг другу. Тогда
При усреднении получим
Таким образом, все найденные на опыте значения силы при усреднении сокращаются, и результат зависит только от первого и последнего опытов. Значит, при такой обработке мы на самом деле не усреднили результаты, полученные в разных опытах, а просто исключили из рассмотрения почти все полученные на опыте данные. Ясно, что такой метод нельзя признать разумным. Математическая причина ошибки очевидна: разумно усреднять результаты только в том случае, если они являются равноточными и независимыми. В первом примере результаты обладали различной точностью, а во втором они не являются независимыми: одно и то же значение силы входит в два соседние равенства. Число примеров при желании можно было бы существенно увеличить. Правильным и удобным методом обработки результатов является графический метод. Изобразим удлинения и силы на графике, как это сделано на рис. 6. На этом рисунке проведена «наилучшая прямая», удовлетворяющая всем требованиям, которые обсуждались ранее. Наклон этой прямой соответствует изменению длины 5,7 · 10–4 см при увеличении силы на 1 Н. Эта цифра может быть прямо подставлена в формулу для вычисления модуля упругости. При рекомендуемом методе графической обработки результатов – при проведении прямой на глаз – учитываются все точки графика. При этом точки, лежащие по его краям, оказываются более существенными, как это и должно быть. Математически этот способ эквивалентен методу «наименьших квадратов», о котором шла речь в начале § 9. Большим преимуществом графического метода является его простота. Сделаем еще одно замечание о построении таких графиков. Часто случается, что начальная точка искомой зависимости хорошо известна и лежит в начале координат. Как бы ни была сложна зависимость тока, проходящего, через проводник, от приложенного к нему напряжения, можно быть уверенным, что при отсутствии напряжения нет и тока (мы предполагаем, что в цени не возникает термо-э. д. с.). При отсутствии силы нет удлинений. Если чайник не нагревать и не охлаждать, то изменение его температуры равно пулю, и т. д. Во всех этих случаях нулевая точка не просто известна,– она является самой надежной из всех, которые используются при обработке результатов. Задача о проведении наилучшей прямой сводится в этом случае к подбору параметра в формуле y =kx. (19) В общем случае нужно найти параметры а и b в формуле y=a+bx (20) Приведем правила для определения погрешностей, которые следует приписывать графически найденным параметрам прямой линии. Пусть прямая описывается формулой (20). Чтобы найти погрешность в определении параметра а, нужно смещать прямую вниз параллельно самой себе, пока выше нее не окажется вдвое больше точек, чем снизу. Затем следует сместить ее вверх, пока снизу не окажется вдво е больше точек, чем сверху. Пусть смещение между этими прямыми равно Δ а (см. рис. 7). Погрешность в определении а равна
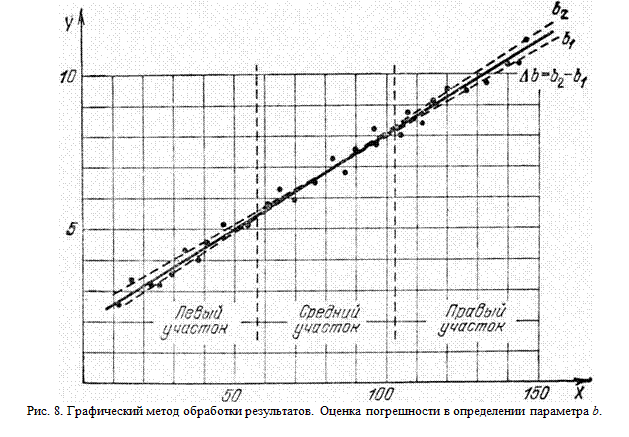
где п – полное число точек на графике. Погрешность в определении параметра b находится аналогичным образом (рис. 8). «Рабочий участок» оси абсцисс (участок, на котором расположены экспериментальные точки) делится на три равные части. Средний участок в дальнейшей работе не участвует. Для определения σ b прямая поворачивается так, чтобы на левом участке выше нее оказалось вдвое больше точек, чем под ней, а на правом участке – наоборот. Затем кривая поворачивается так, чтобы на левом участке 2/3 точек лежали ниже прямой, а на правом – выше нее. Обозначим разницу в угловых коэффициентах этих прямых через Δ b. Тогда
где п – полное число точек на графике.
В заключение приведем правило для нахождения стандартной погрешности при определении параметра k в формуле (19), т. е. при определении наклона прямой, проходящей через начало координат. «Рабочим» участком в этом случае является весь диапазон по оси X от нуля до последней точки. Его следует разбить на три части и самую левую – ближнюю к началу координат – часть во внимание не принимать. Затем нужно провести через начало координат две прямые так, чтобы выше одной из них лежало 2/3 точек, а выше другой – 1/3. Различие в и между этими прямыми определяет Δ k. Стандартная погрешность находится по формуле
где п – полное число точек на графике.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.34.93 (0.011 с.) |

 ,
,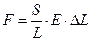 .
. ,
,  , …,
, …,  .
. Каждое из этих данных определяет свое значение Е. Эти значения из-за погрешностей опыта несколько отличаются друг от друга.
Каждое из этих данных определяет свое значение Е. Эти значения из-за погрешностей опыта несколько отличаются друг от друга. . С точностью до постоянного для всех точек коэффициента пропорциональности L/S значение модуля упругости Е равно котангенсу угла, образованного осью абсцисс и прямой, проведенной из начала координат в эту точку. Второе из равенств соответствует прямой, проведенной через точку 2, и т. д. Усреднение величии Е, полученных во всех опытах, означает усреднение котангенсов указанных углов.
. С точностью до постоянного для всех точек коэффициента пропорциональности L/S значение модуля упругости Е равно котангенсу угла, образованного осью абсцисс и прямой, проведенной из начала координат в эту точку. Второе из равенств соответствует прямой, проведенной через точку 2, и т. д. Усреднение величии Е, полученных во всех опытах, означает усреднение котангенсов указанных углов. ,
,  и т. д.
и т. д. ,
,  и т. д.
и т. д. .
. , (21)
, (21)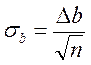 , (22)
, (22)
 ,
,


