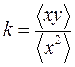Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проведение наилучшей прямой аналитическим методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Параметры наилучшей прямой можно определить не только графически, но и аналитически. Приведем соответствующие формулы. Пусть при значениях хi одной физической величины получены значения уi для другой величины (i =1, 2,..., п). Наилучшая прямая (20) определяется по правилу «наименьших квадратов», т. е. параметрам а и b приписываются такие значения, при которых величина
имеет минимум. При этом получаются следующие формулы для нахождения наилучших значений а и b по измеренным: значениям хi, уi (i = 1, 2,..., п):
где
При расчетах следует помнить, что в числителе первой формулы обычно вычитаются близкие по величине члены, что вызывает необходимость удерживать при вычислениях много значащих цифр. Приведем формулу для определения параметра k: прямой (19), проходящей через начало координат:
Укажем, наконец, формулы для оценки погрешностей параметров а, b и k:
Входящая в формулы (27) дисперсия D (x) определяется по формуле (25). Аналогичным образом вычисляется и D (y). Пример графической обработки экспериментальных данных Поясним изложенное с помощью простого примера.
V=a+bI. Чтобы найти параметры этой прямой, заметим, что ее продолжение.пересекает ось ординат при напряжении 2,1 В. Ток 150 мА достигается при напряжении 10,9 В. Поэтому a = 2,1 В, b = (10,9-2,1)/0,150 = 58,7 В/А. Найдем погрешность указанных значений. В соответствии-с правилом, указанным в тексте, следующем за формулой (20), проведем на рис. 7 две прямые, параллельные основной прямой и обладающие тем свойством, что по одну сторону каждой из них лежит вдвое больше экспериментальных точек, чем по другую,– эти прямые на рис. 7 проведены пунктиром. Расстояние между прямыми Δ а = 0,3 В. Полное число точек на графике составляет 29. По формуле (21) найдем, что погрешность в определении а равна
σa = Δ а / К этой погрешности нужно прибавить ошибку отсчета на миллиметровой бумаге (0,5 мм, т. е. 0,05 В) и ошибку, связанную с погрешностью вольтметра. Последняя равна половине погрешности, соответствующей классу точности вольтметра, т. е. σa, сист = ½ · 2%·15= 0,15 В. Полная погрешность равна σa, полн = При расчете погрешности можно было сразу заметить, что одна из погрешностей, а именно σa, сист, много больше других, и принимать во внимание ее одну. При нашей точности 0,15 и 0,17 не отличаются друг от друга. Скажем несколько слов об ошибке, вносимой в результат погрешностями миллиамперметра. В нашем случав эту погрешность можно не учитывать, потому что измерения проводились с помощью прибора, имеющего высокий класс точности. Если это было бы не так, то токовую погрешность, вносимую миллиамперметром (в нашем случае (1/2)·0,5%·0,15 А = 3,7 · 10–4 А), нужно было бы с помощью параметра b пересчитать в погрешность напряжения (в нашем случае 3,7·10–4·58,7·10–2 В=2,2·10–4 В), возвести в квадрат и внести в подкоренное выражение, служащее для вычисления σa, полн, в качестве одного из слагаемых. Найдем погрешность в определении параметра b. На рис. 8 проведены две прямые в соответствии с рекомендациями, приведенными в тексте, который предшествует формуле (22). С помощью рис. 8 найдем Δ b =b 1 – b 2= 8,2 В/А. Погрешность в определении b согласно (22) равна σb = Δ b / Систематическую часть погрешности оценим, исходя из класса точности вольтметра. Полагая для оценки, что вся ошибка сосредоточена на одном краю шкалы, и учитывая правило, согласно которому погрешность, определяемую классом точности, при расчете ожидаемых ошибок нужно уменьшить вдвое, получим σb, сист = Погрешность отсчета по миллиметровой бумаге вносит в ошибку вклад
Полная погрешность в определении b равна σb, полн = Имеем окончательно а = 2,1 ± 0,2 В, b = 58,7 ± 1,8 В/А. При написании этих значений мы следовали правилу, согласно которому найденное число и его погрешность должны записываться до одного и того же разряда, в нашем случае – включая первый знак после запятой. При написании численного значения а мы округлили погрешность до 0,2 В в соответствии c правилом, сформулированным в § 7.
Посмотрим еще раз на расположение экспериментальных точек на графиках рис. 7 и 8. Эти точки нередко отклоняются от проведенной прямой на 0,2–0,3 В. Хотя такие отклонения не противоречат точности вольтметра, разброс точек явно связан не с ним. В самом деле, экспериментальные точки разбросаны вокруг прямой без всякого порядка. Невозможно предположить, что погрешности прибора ведут себя таким образом: ни сила магнита, ни упругость волоска, ни расположение делений на шкале так беспорядочно «прыгать» не могут. К разбросу точек привела какая-то другая причина, которая не была нами своевременно замечена. Возможно, что эти «прыжки» связаны с плохим качеством контактов,– их следовало бы закрепить или пропаять, а затем повторить опыт. Возможно, что источник питания недостаточно стабилен. Это нужно было бы выяснить и иметь в виду в будущем. Вероятнее же всего, что колебания результатов вызваны плохим контактом в переменном сопротивлении R. Результаты рис. 7 и 8 на самом деле нужно не пускать в обработку, а получить заново, устранив в схеме неисправность. (Мы их оставили здесь в качестве учебного примера.) Заметим, что этот важный вывод мы сделали, анализируя графики рис. 7 и 8. Без графиков к этому заключению прийти было бы намного труднее. Пример аналитической обработки экспериментальных данных Можно найти значения параметров а и b прямой, которая описывает результаты описанного в предыдущем разделе эксперимента, и не прибегая к графикам. Для расчета следует использовать формулы (24) и (27). Поясним ход расчета на примере. В приводимой здесь таблице представлены экспериментальные данные, по которым построены графики рис. 7 и 8:
С помощью калькулятора найдем (I ≡ х, V ≡ у): <х> = 7,9214·10–2 A, < у > = 6,7276 В, < xy > = 0,63236 В·А, <х 2 > = 7,9557 · 10–3 А2, <у 2 > = 51,2114 В2, D(х) = 1,6809 · 10–3 А2, D(у) = 5,9510 В2. По формулам (24) найдем
Найденные погрешности σb и σ a следует сложить с систематическими погрешностями так же, как это было сделано в предыдущем параграфе. Результаты расчета параметров b и а несколько отличаются от результатов, найденных графически, но различие между ними существенно меньше, чем погрешность опытов. Результаты расчета погрешностей отличаются несколько сильнее. Заметим, однако, что для нахождения параметров и их погрешностей, расчетным методом потребовалось много труда, так как вычисление средних значений и дисперсий занимает много времени и приходится производить с большим количеством значащих цифр. Сильное взаимное сокращение членов хорошо видно на примере вычисления σb, где промежуточные результаты выписаны в явном виде. Столь же сильное сокращение членов происходит при вычислении дисперсий х и у. К этому следует прибавить, что аналитический расчет параметров и их погрешностей обычно не избавляет от необходимости строить графики. В самом деле, только взгляд на график убедил нас в том, что вольтамперная характеристика нашего образца хорошо описывается линейной зависимостью. Изучение графика показало нам также, что в схеме имеется нестабильность, которую мы своевременно не заметили. К этим выводам можно прийти и без графика, анализируя табличные данные. Но графический метод позволяет это сделать намного быстрее и нагляднее.
Заключение В заключение еще раз отметим, что паше изложение не претендует ни на полноту, ни на строгость. Оно содержит обзор правил и формул, которые нужно применять, чтобы грамотно обрабатывать полученные экспериментальные данные и приводить их к общепринятому, всем попятному виду. Более глубокое изложение потребуется – и станет возможным – лишь после первых двух курсов обучения, когда будет накоплен достаточный опыт экспериментальной работы и окажется развит необходимый для такого изложения математический аппарат. Поясним сказанное. Мы внимательно рассмотрели в предыдущих параграфах задачу о том, как провести через полученные экспериментальные точки наилучшую прямую и как найти погрешности, возникающие при определении ее параметров. А как проводить наилучшую гиперболу? Как найти параметры кривых, если результат опыта описывается суммой двух экспонент с разными коэффициентами и с различными – заранее не известными – показателями (к такой задаче часто приводит анализ радиоактивного распада), и т. д.? При расчете погрешностей мы рекомендовали пользоваться формулой (4) в том случае, если число измерений равно хотя бы четырем. Существует теория (распределение Стьюдента), которая позволяет получать оценки (не очень, впрочем, надежные) и при меньшем числе измерений. Мы не касались этого вопроса. Мы не рассмотрели и другую важную задачу. Прежде чем находить параметры наилучшей прямой (или другой какой-нибудь заданной зависимости), следует убедиться в том, что полученный набор экспериментальных значений действительно может быть описан прямолинейной зависимостью (или зависимостью другого наперед заданного вида), а не требует привлечения более сложных формул. В начале § 12 мы сказали, что взгляд на рис. 7 убеждает нас в том, что вольтамперная характеристика нашего образца – в рассмотренном диапазоне значений – может быть описана линейной зависимостью. Взгляд на рис. 7, действительно, в этом убеждает. Ну, а если кто-нибудь усомнится, то как его убедить? Поставленный вопрос, конечно, не может решаться в ту или другую сторону только с помощью интуиции. Необходимо иметь количественные критерии, позволяющие в спорных случаях проверять, наблюдается ли на самом деле более сложная зависимость или можно обойтись простой формулой.
Мы задали здесь эти вопросы не для того, чтобы на них ответить, а с тем, чтобы несколько расширить кругозор студентов. Ответы на эти вопросы могут быть получены, но заниматься этим сейчас не время. Для этого необходимо накопить опыт лабораторной работы и приобрести простейшие навыки обработки экспериментальных результатов. Изложенный здесь материал для этого достаточен. Некоторые разъяснения читатель найдет в Приложении, помещенном в конце книги. Приступать к его изучению следует, однако, не ранее чем в начале второго года обучения. Сводка формул
ПРИЛОЖЕНИЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.153 (0.009 с.) |

 (23)
(23)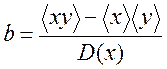 ,
, 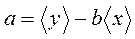 , (24)
, (24) ,
, 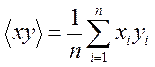 ,
, 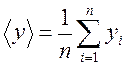 ,
,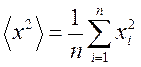 ,
, 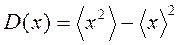 (25)
(25) . (26)
. (26) ,
, 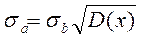 ,
, 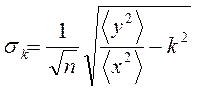 , (27)
, (27)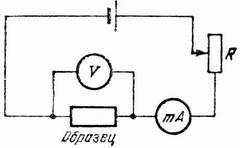 Пусть рис. 7 и 8 (они содержат один и тот же набор экспериментальных точек) изображают результаты исследования вольтамперной характеристики образца на установке, изображенной на рис. 9. Сила тока, проходящего через образец, измеряется миллиамперметром тА (полная шкала 150 мА, класс точности 0,5), а напряжение на нем – вольтметром V (полная шкала 15 В, класс точности 2). Сила тока регулируется резистором R. По оси абсцисс отложена сила тока в миллиамперах, а по оси ординат – напряжение в вольтах. Рассмотрев распределение точек на рисунках, мы видим, что экспериментальные данные в рассматриваемом диапазоне токов и напряжений (10 мА ≤ I ≤ 150 мА, 3 В≤ V ≤ 11 В) хорошо ложатся на прямую линию
Пусть рис. 7 и 8 (они содержат один и тот же набор экспериментальных точек) изображают результаты исследования вольтамперной характеристики образца на установке, изображенной на рис. 9. Сила тока, проходящего через образец, измеряется миллиамперметром тА (полная шкала 150 мА, класс точности 0,5), а напряжение на нем – вольтметром V (полная шкала 15 В, класс точности 2). Сила тока регулируется резистором R. По оси абсцисс отложена сила тока в миллиамперах, а по оси ординат – напряжение в вольтах. Рассмотрев распределение точек на рисунках, мы видим, что экспериментальные данные в рассматриваемом диапазоне токов и напряжений (10 мА ≤ I ≤ 150 мА, 3 В≤ V ≤ 11 В) хорошо ложатся на прямую линию = 0,3/
= 0,3/ 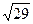 = 0,06 В.
= 0,06 В.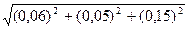 = 0,17 В.
= 0,17 В.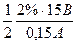 = 1,0 В/А.
= 1,0 В/А.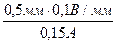 = 0,3 В/А.
= 0,3 В/А. = 1,8 В/A.
= 1,8 В/A.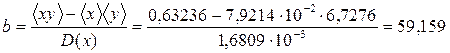 В/А,
В/А, В.
В.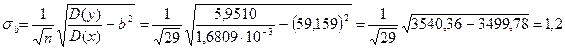 В/А,
В/А, В.
В.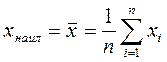
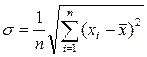 (формула справедлива при п ≥ 4 или 5)
(формула справедлива при п ≥ 4 или 5)
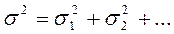
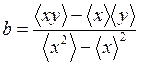 ,
,