
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поправки на мертвое время счетчиков и электронной аппаратурыСодержание книги
Поиск на нашем сайте
При измерении числа событий (например, числа прохождений быстрых частиц через счетчик) приходится вносить поправки, связанные с тем, что после очередного срабатывания счетчик и связанная с ним электронная аппаратура в течение некоторого времени оказываются нечувствительными или не вполне чувствительными к прохождению следующей частицы. Для упрощения задачи обычно пренебрегают периодом неполной чувствительности и делят время на два участка – участок полной и участок нулевой чувствительности. Время нулевой чувствительности обычно называют мертвым временем аппаратуры. В показания счетчиков должна вводиться поправка на мертвое время. Пусть установка за время измерений t зарегистрировала N событий. Обозначим через τ мертвое время установки после импульса. Полное время нечувствительности, очевидно, составило за этот период N τ. Обозначим через N ИСТ число событий, которое сосчитала бы за время t установка, не обладающая мертвым временем. Из этих событий в среднем N ист N τ/ t приходится на мертвое время установки и оказалось пропущенным. Имеем, следовательно,
Формула (П.20) позволяет вносить поправки на мертвое время счетчиков и электронной аппаратуры и находит широкое применение при обработке опытных данных. Следует, однако, помнить, что применимость этой формулы ограничена случаем, когда поправки малы. При больших поправках следует, например, принимать во внимание время неполной чувствительности (частицы, прошедшие в этот период, могут не только не регистрироваться, но и продлевать мертвое время установки). Формула (П.20) не является в этом случае удовлетворительной, и сама нуждается в уточнении. Уточнение формулы, впрочем, обычно не имеет большого смысла, так как при малых поправках все формулы дают практически совпадающие результаты, а при больших поправках вид точной формулы сильно зависит от особенностей применяемой аппаратуры и никогда не бывает сколько-нибудь хорошо известен. Заметим, что вид формулы (П.20) существенно связан со случайным характером распределения регистрируемых частиц во времени. В самом деле, пусть Nτ / t = 0,2. Это означает, что суммарное мертвое время счетчиков составляет пятую часть всего времени их работы. При равномерном распределении импульсов установка успевала бы восстановить свою работоспособность задолго до прихода следующей частицы, и никаких просчетов не наблюдалось бы. Просчеты появляются только из-за нерегулярного прихода следующих частиц. При работе с электронной аппаратурой нередко возникают случаи, когда распределение импульсов во времени, не будучи равномерным, не является все-таки вполне случайным, как это имеет место для прохождений частиц через счетчик Гейгера. Такие случаи возникают, например, при регистрации частиц установкой, содержащей механический регистратор и электронную пересчетную схему. При не очень больших коэффициентах пересчета мертвое время такой установки определяется самым медленно действующим ее звеном – механическим счетчиком. В тех случаях, когда загрузка механического счетчика велика, установка начинает давать просчеты. Эти просчеты не могут, однако, быть учтены с помощью формулы (П.20), так как приходящие с пересчетной схемы на механический счетчик импульсы распределены во времени существенно равномернее, чем импульсы, поступающие на вход пересчетной схемы. Для уяснения вопроса приведем следующее простое рассуждение. Пусть на вход пересчетной схемы в секунду поступает в среднем N случайно распределенных во времени импульсов, и пусть коэффициент пересчета равен n. На выходе пересчетной схемы образуется в среднем N/n импульсов в секунду. Средний промежуток времени, разделяющий два импульса на входе пересчетной схемы, равен, очевидно, 1/ N, а стандартное отклонение этого времени, грубо говоря, равно ему самому (см. ниже). На выходе пересчетной схемы средний промежуток времени t между импульсами составляет n/N. За время t через схему проходит в среднем Nt частиц. Стандартное отклонение этого числа составляет
Наибольший интерес представляет не сама флюктуация времени, а его относительная флюктуация
Как видно из (П.21), величина флюктуации сильно зависит от n. Если при работе без пересчета (n = 1) средняя флюктуация времени между двумя импульсами, как уже отмечалось, равна среднему значению этого времени, то при n = 16 она равна уже всего 1/4, при n = 64 – всего 1/8 этого времени и т. д. Более равномерное распределение импульсов существенно улучшает условия работы механического счетчика, включенного после пересчетной схемы. Формула (П.20), в частности, дает при этом сильно завышенные результаты и непригодна для расчетов.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.253.195 (0.006 с.) |

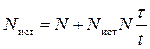 , или
, или 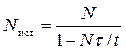 . (П.20)
. (П.20)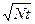 . Разделив
. Разделив 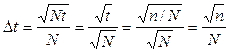 .
.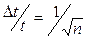 . (П.21)
. (П.21)


