
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов наблюденияСодержание книги
Поиск на нашем сайте
Распределение Пуассона В физике часто приходится встречаться с измерениями, результаты которых представляются в виде целых чисел. Через счетчик Гейгера за время измерения приходит целое – и обычно не очень большое – число частиц. Делящееся ядро распадается на целое число частей. Статистические закономерности, которые имеют место в этом случае, обладают некоторыми особенностями. Рассмотрим счетчик, регистрирующий космические частицы. В то время как число отсчетов счетчика за любой промежуток времени является целым числом, интенсивность ν космического излучения (т. е. отнесенное к единице площади число отсчетов счетчика в секунду, усредненное за очень большой отрезок времени), вообще говоря, целым числом не выражается. Найдем вероятность того, что при интенсивности ν счетчик за время измерения сработает n раз. Будем для простоты считать, что счетчик обладает единичной площадью,– окончательные формулы от этого предположения не зависят. Поскольку мы приступаем к вычислению вероятностей, следует представить себе очень большое число совершенно одинаковых одновременно работающих счетчиков. Некоторая часть их сработает ровно n раз. Доля, составляемая этими счетчиками, по отношению к полному числу счетчиков и равна вероятности того, что через счетчик за время измерения пройдет n частиц. Обозначим полное число счетчиков буквой N. Через них в секунду в среднем проходит N ν частиц, а за небольшое время dt пройдет N ν dt частиц. Если dt достаточно мало, то ни через один из счетчиков за это время не пройдет двух частиц, и наши счетчики можно разбить на два класса: те, через которые за dt прошла частица, и те, через которые не прошла. Последние составляют, конечно, огромное большинство. Число счетчиков, через которые прошла частица, равно, очевидно, числу сосчитанных частиц, т. е. приблизительно N ν dt, а их доля по отношению к полному числу счетчиков составляет N ν dt / N= ν dt. Вероятность того, что за время dt через счетчик пройдет частица, равна, следовательно, ν dt. Это утверждение справедливо только в том случае, если dt очень мало. Вычислим теперь вероятность P 0(t) того, что за время t через счетчик не пройдет ни одной частицы. По определению число таких счетчиков в момент t составляет NP 0(t), а в момент t + dt равно NP 0(t + dt). Это число меньше, чем NP 0(t), потому что за время dt их число убавится на NP 0(t)ν dt. Поэтому NP 0(t + dt) = NP 0(t) – NP 0(t)ν dt, или P 0(t + dt) – P 0(t) = – P 0(t)ν dt, Деля это равенство на dt и переходя к пределу, получим: dP 0/ dt= –ν P 0 Интегрируя, найдем: P 0(t) = – e– ν t. (П.1) При интегрировании было принято во внимание, что в начальный момент времени вероятность найти счетчик, не сработавший ни разу, равна, конечно, единице. Вычислим теперь Pn (t + dt) – вероятность того, что за время: t + dt через счетчик пройдет ровно n частиц. Эти счетчики делятся на две группы. К первой принадлежат те, через которые все n частиц прошли за время t, а за время dt не прошло ни одной. Ко второй группе принадлежат счетчики, через которые за время t прошла n – 1 частица, а последняя частица прошла за время dt. Число первых счетчиков равно NPn (t)(1 – ν dt), а число вторых составляет NPn– 1(t)ν dt. (Каждое из этих выражений состоит из двух сомножителей. Первый из них определяет вероятность нужного числа срабатываний за время t, а второй – вероятность несрабатывания или срабатывания за время dt.) Имеем, следовательно: NPn (t + dt) = NPn (t)(1 – ν dt) – NPn– 1(t)ν dt. Перенесем NPn (t)(1 – ν dt) в левую часть равенства и разделит его на Ndt:
Последовательно применяя полученную рекуррентную формулу к n = 1, n = 2 и т. д., с помощью (П.1) найдем:
Заметим теперь, что ν t, которое мы обозначим через n 0, равно среднему числу частиц, проходящих через счетчик за время t. Наша формула примет вид
Эта формула является окончательной и носит название закона распределения Пуассона. Она определяет вероятность того, что при среднем числе срабатываний n 0 (это число, вообще говоря, не является целым) произойдет именно n срабатываний (n – целое число).
Для иллюстрации на рис. 1 изображено распределение Пуассона для n 0 = 2,6. Ни для какого n величина Pn не равна нулю. Она достигает максимума при n = 2. Вероятность найти n = 0 оказывается довольно велика. Достаточно велика также вероятность того, что счетчик срабатывает 3, 5 и даже 7 раз. Рассмотрим некоторые свойства формулы (П.2). Вычислим, прежде всего, вероятность найти какое угодно значение n:
Этот результат является очевидным, потому что хоть какое-нибудь значение n, конечно, всегда будет найдено на опыте, так что мы вычисляли вероятность достоверного события. Вычислим среднее значение n:
Полученный результат тоже можно было предсказать заранее, поскольку мы исходили из того, что среднее значение n равно n 0. Найдем теперь среднеквадратичное отклонение (стандартную ошибку) величины n. Для этого сначала вычислим дисперсию n (среднее значение квадрата отклонения):
Вычисление суммы в качестве полезного упражнения мы предоставляем читателям. Имеем, следовательно:
Этот результат мы уже использовали ранее без доказательства: стандартная погрешность, допускаемая при измерении числа отсчетов, равна корню квадратному из числа отсчетов. Распределение Гаусса Распределение Гаусса является предельным случаем распределения Пуассона и многих других законов распределения. Рассмотрим распределение Пуассона при больших n 0 и n. Дискретность распределения по n в этом случае теряет свое значение, так как n меняется практически непрерывно. Будем характеризовать отличие n от n 0 с помощью ε, определенного соотношением n = n 0(1 + ε). Подставляя формулу Стерлинга
в выражение (П.2), найдем:
откуда
Вероятность Pn может быть обобщена на непрерывные величины. Чтобы это сделать, заметим, что n – n 0 равно отклонению найденной на опыте величины n от среднего значения n 0. Обозначим это отклонение через x: x = n – n 0. Заменим n 0 стандартным отклонением σ с помощью (П.3). Наконец, заметим, что Pn можно интерпретировать как вероятность того, что найденное на опыте значение n лежит в интервале между n – ½ и n + ½. Этому интервалу соответствует Δ x = 1. Произведя указанные замены и перейдя от обозначения Pn к обозначению P (x), получим:
Распределение (П.5) носит название распределения Гаусса. P (x) определяет вероятность того, что величина x попадает в единичный интервал Δ x, окружающий точку х. Выбирая вместо единичного бесконечно малый интервал dx, найдем:
С помощью (П.6) нетрудно найти вероятность того, что для x будет найдено значение, лежащее между x 1 и x 2, где x 1 и x 2 – любые числа. Как нетрудно понять,
Интеграл (П.7) в элементарных функциях не выражается. Он может быть вычислен с помощью таблиц интеграла вероятности erf(x):
Нетрудно показать, что
График функции erf(x) изображен на рис. 3. Функция erf(x) антисимметрична относительно точки x = 0, так что erf(– x) = – erf(x). (П.10) С помощью таблиц или графика erf(x) нетрудно найти вероятность того, что для искомой величины будет найдено значение, лежащее между –σ и σ, между –2σ и 2σ и между любыми другими значениями x:
Вероятность найти величину x в заданных пределах при увеличении ширины интервала быстро приближается к единице. Так.
и т. д. Из этого факта часто делается неверное утверждение о том, что погрешности, превосходящие 3σ, а тем более 4σ, практически никогда не встречаются. На самом деле они встречаются не так уж редко. Это происходит потому, что истинные распределения погрешностей очень разнообразны и никогда в точности не следуют закону Гаусса. Эти распределения обычно считают гауссовыми за неимением лучшего. В области малых отклонений от среднего закон распределения Гаусса по большей части неплохо оценивает вероятности различных встречающихся на практике отклонений, а в области больших отклонений описывает их плохо, и чем отклонения больше – тем хуже. Метод наименьших квадратов Метод наименьших квадратов позволяет находить по результатам эксперимента наилучшие значения параметров, входящих в формулы, вид которых считается известным. Пусть, например, исследуется растяжение тела. Обозначим значения приложенной к телу силы через yi (i –номер опыта), а значения удлинений – через xi. Считается известным, что сила, действующая на образец, и его удлинение связаны между собой законом Гука: y = kx. (П.11) Неизбежные погрешности опыта приводят к тому, что точки (xi, yi) не лежат на одной прямой. Метод наименьших квадратов позволяет найти наилучшее значение k аналитическим методом. В качестве такого значения в методе наименьших квадратов принимается значение, при котором величина
(σ i – среднеквадратичная погрешность i -го измерения) имеет минимум. Иначе говоря, ищется значение k, при котором dφ/dk обращается в нуль. Имеем:
Легко видеть, что мы пришли к линейному относительно k выражению, которое легко может быть решено. Приведем результат для случая, когда все σ i равны друг другу. Из (П.13) следует в этом случае:
Разделив обе части этого уравнения на п, получим:
где угловые скобки, как обычно, обозначают средние значения. Из этого уравнения находим:
Формула (П.14) определяет k с некоторой погрешностью, величина которой может быть оценена по разбросу экспериментальных данных. Вычисления дают:
В формулу (П.15) следует подставлять значение k, полученное из (П.14). Аналогичным образом могут быть получены формулы для случая, когда стандартные погрешности σ i не равны друг другу, и формулы для определения параметров в формулах более сложных, чем (П.11). Формулы для определения параметров в формуле y = a + bx. (П.16) приведены выше. Скажем несколько слов о случаях, когда зависимость y от x описывается более сложными формулами, например функцией произвольного вида: у = f (x, а, b, с,...), (П.17) где а, b, с,... – искомые параметры. Если погрешности измерения величины yi описываются законом Гаусса, то решение задачи находится путем отыскания минимума величины
для чего приравниваются нулю частные производные dφ/da, dφ/db, dφ/dc и т. д. Легко видеть, что при этом возникает столько уравнений сколько имеется подлежащих определению величин а, b, с,... Эти уравнения в общем случае нелинейны и могут быть решены только численно. Если погрешности в измерении yi не описываются законом Гаусса, то задача становится еще более сложной и приводится к отысканию экстремума функций существенно более сложных, чем (П.18). Соответствующий метод носит название метода наибольшего правдоподобия. Мы этого случая рассматривать не будем. В том случае, когда в формуле подбирается не один, а несколько параметров, решение приобретает новые важные черты. Погрешности параметров обычно оказываются связанными друг с другом: отклонения сразу по двум параметрам – при определенном соотношении между ними – могут оказаться более вероятными, чем отклонение только по одному параметру. При решении одномерной задачи указывают среднеквадратичную погрешность – погрешность, которая при гауссовом распределении превышается, как мы уже отмечали, приблизительно в одной трети случаев. В двумерной задаче нужно в плоскости искомых параметров проводить кривую, выделяющую соответствующую область. При гауссовых распределениях эта кривая является эллипсом. Как известно, величина и положение эллипса определяются не двумя, а тремя числами, например размерами его полуосей и углом их поворота. При измерениях, в которых следует определить два параметра, задание погрешностей требует поэтому, строго говоря, указания не двух, а трех чисел, которые образуют квадратную симметричную «матрицу ошибок». Мы не будем более развивать эту тему и отошлем интересующихся к литературе. § 4. Критерии значимости. Метод χ2.
Сформулированная сейчас задача в применении к закону Гука представляется несколько искусственной. В этом случае лучше всего попросту повторить опыт, уменьшив экспериментальные ошибки, и вопрос решится сам собой. Встречаются, однако, случаи, когда такое повторение опыта оказывается затруднительным или даже невозможным. Так бывает, например, при опытах с редкими частицами в космических лучах или на ускорителях, когда повторение опыта требует нескольких лет работы или попросту невозможно. Возможно, более полная интерпретация имеющихся данных становится в этом случае особенно существенной. Общий вопрос, который возникает в таких случаях, сводится обычно к следующему. На графике, изображающем некоторую зависимость, точки легли не вполне регулярно. Следует ли придавать значение наблюденным отступлениям от гладкой кривой? Совместима ли с экспериментальными данными гипотеза о том, что искомая зависимость на самом деле является гладкой (или даже прямолинейной), или эти данные указывают на негладкий, аномальный ход кривой? Исследование проблемы достоверности гипотез производится обычно с помощью критериев значимости. Одним из наиболее удобных критериев значимости является так называемый «критерий χ2»• В предыдущем параграфе мы рассматривали метод наименьших квадратов, с помощью которого можно, например, провести через экспериментальные точки наилучшую прямую. Исследуем теперь вопрос о том, насколько данные, использованные для проведения этой прямой, согласуются с представлением о том, что рассматриваемая прямолинейная зависимость действительно имеет место. Единственной мерой, которая может быть использована для расчета, является, естественно, точность, с которой экспериментальные точки удовлетворяют предполагаемому закону. В методе χ2 в качестве такой меры принимается сумма квадратов отклонений от предполагаемой зависимости:
Отклонения экспериментальных точек от ожидаемых значений, как мы видим, выражаются в долях стандартной ошибки данного измерения. Найденное значение χ2 должно быть сопоставлено с теорией. Это делается с помощью таблицы 1. В таблице для разного числа степеней свободы (числом степеней свободы в этом случае называется число измерений без одного, если гипотеза не содержит определяемых из опыта коэффициентов; число измерений без двух, если из опыта находится один коэффициент, например наклон прямой, и т. д.) приведены значения χ2 для ряда чисел p. Для 10 степеней свободы находим из таблицы, что χ2 = 2,6 для p = 99, χ2 = 3,9 для p = 95, х2 = 7,3 для p = 70, χ2 = 23,2 для p = 1 и т. д. Это означает, что в том случае, если гипотеза справедлива, рассчитанное по (П.19) значение χ2 с вероятностью 99% (p = 99) окажется больше 2,6, с вероятностью 95% (p = 95) больше. 3,9, с вероятностью 70%.больше 7,3, с вероятностью 1% больше 23,2 и т. д. Пусть мы найдем в результате расчета по формуле (П.19) χ2 = 3,5. Такое значение χ2 должно наблюдаться больше чем в 95% случаев; отклонение наших данных от ожидаемой прямолинейной зависимости является в этом случае совершенно несущественным. Если бы мы нашли в результате расчета χ2 = 18, сопоставление с таблицей показало бы нам, что такие отклонения следует ожидать только в 5% случаев. Существование прямолинейной зависимости и в этом случае нельзя считать исключенным, но должно быть поставлено под сомнение. Естественно в этом случае повторить опыт, чтобы получить более ясный результат. Если бы χ2 оказалось равным 30 (вероятность получить на опыте такое значение ≈0,1%), можно было бы утверждать, что проверяемая гипотеза почти наверное является ошибочной. При сравнении отклонений с таблицей обычно применяют следующую терминологию: если найденная из опыта величина χ2 должна наблюдаться с вероятностью, заключенной между 1 и 5%, отклонения называются почти значимыми, если вероятность заключена между 0,1 и 1%,– значимыми и, наконец, если вероятность обнаружить найденное значение χ2 оказывается меньше 0,1%, отклонения являются высокозначимыми. При вероятности больше 5% следует считать, что экспериментальные данные недостаточны для того, чтобы отвергнуть гипотезу. На этом мы заканчиваем краткое изложение общих методов обработки результатов наблюдений. Более подробные сведения могут быть найдены в специальных книгах. Таблица 1. Распределение χ2 p – вероятность (в%) найти на опыте значение χ2, большее, чем указано в таблице; n – число степеней свободы системы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.009 с.) |


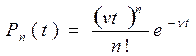 .
.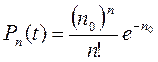 (П.2)
(П.2) Закон распределения Пуассона записан в такой форме, что из всех характеристик работы счетчика осталась только одна – его среднее число срабатываний за время измерения. Ни само время измерения, ни, тем более, площадь счетчика, которую мы вначале для простоты положили равной единице, в формулу не входят. Равным образом в формуле никак не отражено то обстоятельство, что мы рассматривали счетчик Гейгера, регистрирующий космическое излучение. С равным успехом эта формула применима к числу соединений на телефонной станции или к любой другой задаче, где число случаев является целым, а их появление в любой момент времени не зависит от числа случаев, произошедших ранее (независимые события).
Закон распределения Пуассона записан в такой форме, что из всех характеристик работы счетчика осталась только одна – его среднее число срабатываний за время измерения. Ни само время измерения, ни, тем более, площадь счетчика, которую мы вначале для простоты положили равной единице, в формулу не входят. Равным образом в формуле никак не отражено то обстоятельство, что мы рассматривали счетчик Гейгера, регистрирующий космическое излучение. С равным успехом эта формула применима к числу соединений на телефонной станции или к любой другой задаче, где число случаев является целым, а их появление в любой момент времени не зависит от числа случаев, произошедших ранее (независимые события). .
.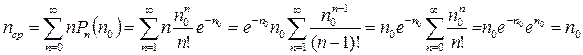 .
. .
.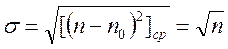 (П.3)
(П.3)
 ,
, . (П.4)
. (П.4) . (П.5)
. (П.5) . (П.6)
. (П.6)
 . (П.7)
. (П.7) . (П.8)
. (П.8) . (П.9)
. (П.9)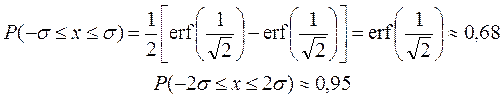 .
. ,
, (П.12)
(П.12) . (П.13)
. (П.13)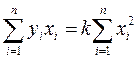 .
. ,
, . (П.14)
. (П.14) . (П.15)
. (П.15) , (П.18)
, (П.18) Вернемся к опыту по исследованию упругих свойств металлического стержня. Пусть результаты опытов изображаются точками на рис. 4. Первый же взгляд на график убеждает нас в том, что зависимость удлинения от нагрузки является линейной или почти линейной. В самом деле, прямая, проведенная на рис. 4 сплошной линией, не противоречит экспериментальным данным. Им не противоречит, однако, и изогнутая штриховая линия. Более того, эта линия даже несколько лучше удовлетворяет экспериментальным данным, чем прямая. Мы хотели бы, однако, думать, что истинная связь удлинения и нагрузки все-таки является прямолинейной. Задача сводится к отысканию критерия, позволяющего судить о том, является ли представление искомой зависимости в виде прямой линии достаточно хорошим или экспериментальные данные заставляют отдать предпочтение криволинейной зависимости, например зависимости, изображенной штриховой линией.
Вернемся к опыту по исследованию упругих свойств металлического стержня. Пусть результаты опытов изображаются точками на рис. 4. Первый же взгляд на график убеждает нас в том, что зависимость удлинения от нагрузки является линейной или почти линейной. В самом деле, прямая, проведенная на рис. 4 сплошной линией, не противоречит экспериментальным данным. Им не противоречит, однако, и изогнутая штриховая линия. Более того, эта линия даже несколько лучше удовлетворяет экспериментальным данным, чем прямая. Мы хотели бы, однако, думать, что истинная связь удлинения и нагрузки все-таки является прямолинейной. Задача сводится к отысканию критерия, позволяющего судить о том, является ли представление искомой зависимости в виде прямой линии достаточно хорошим или экспериментальные данные заставляют отдать предпочтение криволинейной зависимости, например зависимости, изображенной штриховой линией. . (П.19)
. (П.19)


