
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости и прямойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
 Пусть в пространстве задана декартова прямоугольная система координат Oxyz. Плоскость P вполне определяется заданием ее точки Пусть в пространстве задана декартова прямоугольная система координат Oxyz. Плоскость P вполне определяется заданием ее точки 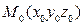 и ненулевого вектора и ненулевого вектора 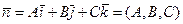 , перпендикулярной плоскости. Вектор , перпендикулярной плоскости. Вектор  называется нормальным вектором плоскости Р. Пусть называется нормальным вектором плоскости Р. Пусть  - произвольная точка Р; - произвольная точка Р;  - ее радиус-вектор, a - ее радиус-вектор, a  - радиус-вектор точки М0 (рис.1). Тогда - радиус-вектор точки М0 (рис.1). Тогда  лежит в плоскости Р, а значит перпендикулярен вектору лежит в плоскости Р, а значит перпендикулярен вектору  . Это возможно тогда и только тогда (см.свойство 5 скалярного произведения), когда . Это возможно тогда и только тогда (см.свойство 5 скалярного произведения), когда
Уравнение (1) называется векторным уравнением плоскости. Так как
Уравнение (2) задает плоскость Р, которая проходит через заданную точку
Пример 1. Найти уравнение плоскости, проходящей через точки М1(1,-1,0), М2(2,1,-3), М3(-1,0,1). Решение. Уравнение плоскости, проходящей через точку М1 имеет вид
Так как векторы
Таким образом, А=B=С=5 и искомое уравнение имеет вид
Теорема. Уравнение
где Уравнение (3) называется общим уравнением плоскости. Доказательство. Известно, что любая плоскость задается уравнением (2). Раскрывая скобки в (2), получаем уравнение вида (3). Докажем теперь, что уравнение вида (3) определяет некоторую плоскость. Уравнение (3) имеет бесконечно много решений (если, например,
Вычитая из (3) равенство (4), получим равносильное (3) уравнение (2), которое задает плоскость, проходящую через точку Заметим, что если в уравнении (3) D=0, то плоскость Р, определяемая этим уравнением, проходит через начало координат. Если, например, А=0, то Р параллельна оси Оx, так как нормальный вектор (0, В, С) плоскости Р лежит в плоскости Оx. Уравнения x=0, y=0, z=0 соответственно определяют плоскости Оyz, Oxz, Oxy. Пусть плоскости Р1 и Р2 заданы соответственно уравнениями
Тогда угол
Плоскости Р1 и Р2 перпендикулярны тогда и только тогда, когда перпендикулярны их нормальные векторы
Плоскости Р1 и Р2 параллельны тогда и только тогда, когда их нормальные векторы Пусть даны точка
Прямая в пространстве. Рассмотрим систему уравнений
каждое из которых задает плоскость. Если эти плоскости не параллельны, то система (5) определяет прямую, т.е. координаты точек этой прямой, только они удовлетворяют системе (5). Уравнения (5) называют общими уравнениями прямой. Положение прямой L в пространстве вполне определяется заданием ее точки
Уравнение (6) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой L. Приравняв координаты в уравнении (6), получим
Уравнения (7) называются параметрическими уравнениями прямой. При изменении параметра t изменяются координаты x, y, z и точка M(x,y,z) перемещается по прямой. Если m, n, p
Это каноническое уравнение прямой. Если, например,
также допускается. Она означает, что
Пример 2. Написать каноническое уравнение прямой, проходящей через точки Решение. За направляющий вектор этой прямой можно взять вектор
т.е.
Сформулируем простейшие факты о прямой на плоскости Оxy. 1. Общее уравнение прямой:
2. Если
3. Если В=0, то (9) примет вид x=a. 4. Каноническое уравнение прямой имеет вид
Здесь вектор 5. Расстояние от точки (x0,y0) до прямой
Отметим еще, что угол между двумя прямыми равен углу между двумя их нормальными (или направляющими) векторами. Прямые
Пример 3. Дан Найти уравнения медианы, высоты и биссектрисы, проведенных из А. Решение. Пусть D – середина отрезка ВС. Тогда
направляющий вектор медианы. Вектор
единичный вектор в направлении
единичный вектор в направлении
МАТРИЦЫ
Рассмотрим прямоугольную числовую таблицу (матрицу)
которая имеет размеры Элемент Пример 1. Матрица
имеет две строки и четыре столбца (размеры 2×4). Если m=n, то А называется квадратной матрицей порядка n. Две матрицы считаются равными, если они имеют одинаковые размеры и равны их элементы, стоящие на одинаковых местах. Произведением матрицы Пример 2.
Если
Пример 3.
Пусть А=(
Пример 4.
Пример 5. Если
то произведение АВ не определено. Пример 6.
Таким образом, коммутативность умножения матриц в общем случае не имеет место. Можно проверить, что умножение матриц ассоциативно, т.е.
во всех случаях, когда умножение определено, а сложение и умножение связаны законами дистрибутивности:
Можно сказать также, что если А и В – две квадратные матрицы, то
Рассмотрим квадратные матрицы вида:
Такие матрицы называются единичными, так как если А – произвольная квадратная матрица порядка n, Е – единичная матрица порядка n, то АЕ=ЕА=А.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.239.65 (0.008 с.) |

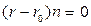 (1)
(1) , то в силу теоремы из раздела 4 уравнение (1) равносильно уравнению
, то в силу теоремы из раздела 4 уравнение (1) равносильно уравнению (2)
(2) перпендикулярно вектору нормали
перпендикулярно вектору нормали 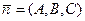 . Координаты точек плоскости Р и только они удовлетворяют уравнению (2).
. Координаты точек плоскости Р и только они удовлетворяют уравнению (2).
 лежат в искомой плоскости, то их векторное произведение
лежат в искомой плоскости, то их векторное произведение 
 или
или 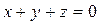 .
. (3)
(3) , определяет в пространстве некоторую плоскость и наоборот любая плоскость задается уравнением вида (3).
, определяет в пространстве некоторую плоскость и наоборот любая плоскость задается уравнением вида (3). , то
, то 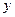 и
и  можно придать любые значения, а затем найти
можно придать любые значения, а затем найти  ). Пусть
). Пусть  ,
,  ,
, 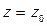 - одно из них, тогда
- одно из них, тогда (4)
(4)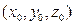 перпендикулярно вектору (А,В,С). Теорема доказана.
перпендикулярно вектору (А,В,С). Теорема доказана.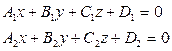
 между плоскостями Р1 и Р2 равен углу между их нормальными векторами
между плоскостями Р1 и Р2 равен углу между их нормальными векторами  и
и 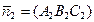 т.е.
т.е.
 , т.е.
, т.е.
 .
.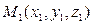 и плоскость Р, имеющая уравнение
и плоскость Р, имеющая уравнение  . Расстояние
. Расстояние  между ними, т.е. длина перпендикуляра, опущенного из этой точки М1 на плоскость Р, определяется формулой
между ними, т.е. длина перпендикуляра, опущенного из этой точки М1 на плоскость Р, определяется формулой

 (5)
(5) и параллельного ей вектора
и параллельного ей вектора  (рис.2), который называется направляющим вектором прямой L. Пусть
(рис.2), который называется направляющим вектором прямой L. Пусть  произвольная точка прямой L,
произвольная точка прямой L,  . Так как векторы
. Так как векторы  и
и  коллинеарны, то
коллинеарны, то  или
или (6)
(6)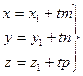 (7)
(7) 0, то из (7) непосредственно получаем
0, то из (7) непосредственно получаем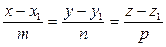 (8)
(8) , то запись (условная)
, то запись (условная)
 для всех точек прямой L (см.(7))
для всех точек прямой L (см.(7))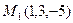 и
и  .
. . Таким образом,
. Таким образом,  ,
,  и в силу (8) искомое уравнение
и в силу (8) искомое уравнение

 Очевидно, что угол между двумя прямыми равен углу между их направляющими векторами, а условия параллельности и перпендикулярности двух прямых равносильны соответственно условиям коллинеарности и перпендикулярности их направляющих векторов.
Очевидно, что угол между двумя прямыми равен углу между их направляющими векторами, а условия параллельности и перпендикулярности двух прямых равносильны соответственно условиям коллинеарности и перпендикулярности их направляющих векторов.
 (9)
(9) , определяет на плоскости некоторую прямую. Наоборот, всякая прямая задается уравнением вида (9). Вектор (А,В) перпендикулярен прямой (он называется нормальным вектором прямой).
, определяет на плоскости некоторую прямую. Наоборот, всякая прямая задается уравнением вида (9). Вектор (А,В) перпендикулярен прямой (он называется нормальным вектором прямой). , то из (9) получаем уравнение прямой с угловым коэффициентом
, то из (9) получаем уравнение прямой с угловым коэффициентом , где
, где  (рис.3).
(рис.3). (10)
(10) параллелен прямой (направляющий вектор), а точка М(x1,y1) лежит на прямой.
параллелен прямой (направляющий вектор), а точка М(x1,y1) лежит на прямой. определяется формулой
определяется формулой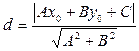
 параллельны (перпендикулярны) тогда и только тогда, когда
параллельны (перпендикулярны) тогда и только тогда, когда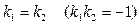 .
. .
. -
- перпендикулярен вектору
перпендикулярен вектору  , так как
, так как  . Поэтому
. Поэтому  - направляющий вектор высоты. Далее,
- направляющий вектор высоты. Далее,
 , а
, а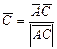
 , поэтому b+c – направляющий вектор биссектрисы. Остается применить формулу (10).
, поэтому b+c – направляющий вектор биссектрисы. Остается применить формулу (10).
 (m строк, n столбцов). Сокращенная запись:
(m строк, n столбцов). Сокращенная запись: 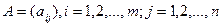
 матрицы А расположен в i – й строке и j – м столбце.
матрицы А расположен в i – й строке и j – м столбце.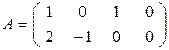
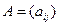 на число α называется матрица
на число α называется матрица  , элементы которой получаются из элементов матрицы А умножением на
, элементы которой получаются из элементов матрицы А умножением на  .
. 
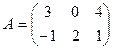 ,
, 
 ,
,  - матрицы одинакового размера, матрица того же размера
- матрицы одинакового размера, матрица того же размера 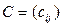 ,
,  называется суммой матриц А и В (С=А+В).
называется суммой матриц А и В (С=А+В).
 ) – матрица размера n×p, т.е. число столбцов матрицы А равно числу строк матрицы В. Произведением матрицы А на В называется матрица С=(
) – матрица размера n×p, т.е. число столбцов матрицы А равно числу строк матрицы В. Произведением матрицы А на В называется матрица С=( ) размера m×p (C=A∙B), элементы которой находят по следующему правилу: элемент i –й строки и j –ого столбца матрицы С равен сумме произведений элементов i –й строки матрицы А на соответствующие элементы j –ого столбца матрицы В, т.е.
) размера m×p (C=A∙B), элементы которой находят по следующему правилу: элемент i –й строки и j –ого столбца матрицы С равен сумме произведений элементов i –й строки матрицы А на соответствующие элементы j –ого столбца матрицы В, т.е. ,
, 

 ,
, ;
;
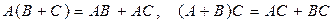 .
. (1)
(1)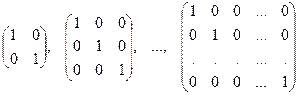 .
.


