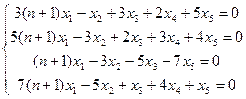Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Привеление системы линейных уравнений к виду, удобному для итерацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Процессы последовательных приближений и Зейделя для линейной системы Х = Таким образом, для сходимости вышеуказанных итерационных процессов достаточно, чтобы значения элементов Применяя элементарные преобразования, линейную систему AX = B можно заменить такой эквивалентной системой Х =
Пример 1. Привести данную систему линейных уравнений к виду, удобному для итерации: Решение. 1) Из данной системы выделяем уравнения с коэффициентами, модули которых больше суммы модулей основанных коэффициентов системы. Каждое выделенное уравнение выписываем в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным. В уравнении (Б) коэффициент при 2) Из оставшихся неиспользованных уравнений системы оставляем линейно независимые между собой комбинации. Так, за первое уравнение новой системы можно взять линейную комбинацию (2В)+(А), тогда имеем За третье уравнение новой системы можно принять линейную комбинацию (2А)-(Б), т.е. 3) В итоге получаем преобразованную систему линейных уравнений (1), (2), (3), эквивалентную исходной и удовлетворяющую условиям сходимости итерационного процесса: Приведя систему (*) к нормальному виду, имеем Остается решить систему одним из итерационных методов.
ИСПРАВЛЕНИЕ ЭЛЕМЕНТОВ ПРИБЛИЖЕННОЙ ОБРАТНОЙ МАТРИЦЫ Пусть дана неособенная матрица А и требуется найти ей обратную А -1. Предположим, что мы получили приближенное значение обратной матрицы Тогда для улучшения точности воспользуемся методом последовательных приближений следующим образом. За нулевое приближение обратной матрицы А -1 принимаем значение D 0 погрешность которого есть матрица
Дальнейшие последовательные приближения будем строить по формуле
и соответствующая погрешность Если все элементы матрицы Оценка погрешности данного метода имеет вид где под нормой понимается норма 1 и норма 2. Процесс уточнения элементов обратной матрицы
исправить элементы приближенной обратной матрицы с точностью до 10-5 . Решение. 1) Методом Гаусса находим приближенную обратную матрицу
Далее, получаем
Так как 2) Пользуясь формулой (1), находим следующее приближение D 1. Имеем
3) Аналогичным образом получим приближение D 2
Следовательно,
Упражнения 1. Вычислить АВ, если а) б) Ответы: а)
2. Вычислить 2(А + В)(2 В - А), если а) б) Ответы: а) 3. Найти произведение XY, если а) в) Ответы: а)
4. Найти произведение АХ, если а) б) Ответы: а)
5. Вычислить определители а) в) Ответы: а) 22; б) -26; в) 4279,1. 6. Вычислить А -1 для следующих матриц: а) в)
Ответы: а) в)
7. Для матриц
вычислить норму 1, 2 и норму 3. Ответы: а)
8. Найти АВ, где
Двумя способами: а) разбив А и В на квадратные клетки; б) разбив А и В на клетки окаймлением
9. Вычислить А -1, применив разбиение на квадратные клетки и окаймление, если: а) Ответы: а) 10. Матрицы, заданные в упр. 9, разложить на произведение двух треугольных и обратить их, применяя разложение матриц на произведение двух треугольных. Ответы: а)
б)
11. Решить матричные уравнения: а) Ответы: а)
12. Следующие системы линейных уравнений решить по формулам Крамера: а) Ответы: а)
13. Решить следующие системы по схеме Гаусса: а)
Ответы: а)
14. С точность до 0,001 решить следующие системы по схеме Гаусса: а) Ответы: а)
15. Вычислить определители по схеме Гаусса:
а)
Ответы: а) d =88; б) d =2111,97.
16. Обратить следующие матрицы по схеме Гаусса:
а) Вычисления вести с тремя десятичными знаками, ответ округлить до двух десятичных знаков. Ответы: а) 17. Решить следующие системы линейных уравнений с точностью до 0,01 методом последовательных приближений, предварительно определив необходимое количество шагов: а) Ответы: а) 18. Системы линейных уравнений из упр. 17 решить методом Зейделя, предварительно определив необходимое количество шагов.
Задания для самостоятельной работы. N-номер варианта студента, n – последняя цифра номера варианта N студента.
Задание 1. Вычислить определители
Задание 2. Решить систему линейных уравнений по формулам Крамера и матричным методом
Задание 3. Даны векторы
Найти: 1) ( 2) ( 3) 4) площадь параллелограмма, построенного на векторах
5) объем параллелепипеда, построенного на векторах 6) определить, какую тройку образуют векторы
Задание 4. Даны координаты четырех точек A,B,C,D: А(7n;2;4), В(7n;-1;-2), С(3n;3;1), D(-4n;2;1). 1) написать уравнение плоскости 2) написать уравнение плоскости 3) найти угол между плоскостями 4) найти уравнение и длину высоты, опущенной на грань АВС; 5) найти координаты точки D, симметричной относительно плоскости 6) найти площадь грани АВС; 7) найти объем пирамиды АВСD; 8) найти угол между ребрами АВ и АС.
Задание 5. Найти произведение матриц А и В:
Задание 6. Для матрицы
вычислить норму 1, 2 и норму 3.
Задание 7. Дана система векторов α1; α 2, α 3, α 4, α 5, α 6, в которой α1=(7(n+1),0,9(n+1),16(n+1)), α2(3,1,4,8), α 3 = (0, 1, 1, 2), α 4= (1, 1, 1, 3), α 5 = (1, 0, -2, -1), α 6 = (1, 0, 1, 2). Дополнить линейно независимую часть α 1, α2 до базиса системы векторов α 1, α 2, α 3, α 4, α 5, и все векторы, не вошедшие в базис, разложить по базису. Задание 8. Найти общее решение системы линейных уравнений методом Гаусса.
Задание 9. Найти фундаментальный набор решений однородной системы линейных уравнений.
Задание 10. Найти собственные значения и собственные векторы матрицы.
Задание 11. Найти линейное преобразование неизвестных, приводящее квадратичную форму, заданную своей матрицей, к каноническому виду. Выяснить, является ли квадратичная форма знакоопределенной.
Задание 12. Решить следующую систему линейных уравнений с точностью до 0,01 методом последовательных приближений, предварительно определив необходимое количество шагов:
Задание 13. Систему линейных уравнений задания 12 решить методом Зейделя, предварительно определив необходимое количество шагов.
Задание 14. Решить транспортные задачи согласно своему варианту N. Вариант 1
Вариант2
Вариант3
Вариант4
Вариант5
Вариант6
Вариант 7
Вариант 8
Вариант9
Вариант10
Вариант11
Вариант12
Вариант13
Вариант14
Вариант15
Вариант16
Вариант17
Вариант18
Вариант19
Вариант20
Вариант21
Вариант22
Вариант23
Вариант24
Вариант25
Вариант26
Вариант27
Вариант28
Вариант 29
Вариант 30
Вариант 31
Вариант 32
Вариант 33
Вариант 34
Вариант 35
Вариант 36
Вариант 37
Вариант 38
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 +
+  Х сходятся к единственному решению независимо от выбора начального вектора, если
Х сходятся к единственному решению независимо от выбора начального вектора, если
 матрицы
матрицы  при
при  были небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы AX = B модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. если мы имеем систему
были небольшими по абсолютной величине. Это равносильно тому, что если для линейной системы AX = B модули диагональных коэффициентов каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов), то итерационные процессы для этой системы сходятся, т.е. если мы имеем систему  причем
причем 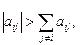 то процессы последовательных приближений и Зейделя для данной системы сходится.
то процессы последовательных приближений и Зейделя для данной системы сходится.
 по модулю больше суммы модулей остальных коэффициентов. Принимаем уравнение (Б) за второе уравнение новой системы.
по модулю больше суммы модулей остальных коэффициентов. Принимаем уравнение (Б) за второе уравнение новой системы. (1)
(1) (2)
(2) . (3)
. (3) (*)
(*)


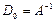 .
.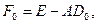
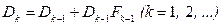 (1)
(1)
 удовлетворяют неравенству
удовлетворяют неравенству  где n- порядок матрицы и
где n- порядок матрицы и  то процесс итерации заведомо сходится.
то процесс итерации заведомо сходится.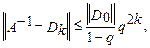 (2)
(2)



 то итерационный процесс сходится.
то итерационный процесс сходится.
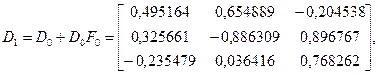
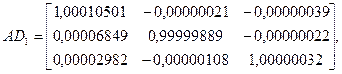
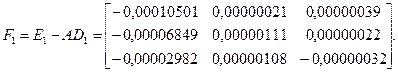






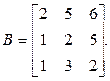
 б)
б) 

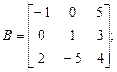


 б)
б) 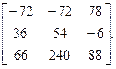

 б)
б) 



 б)
б)  в) 409.
в) 409.



 б)
б) 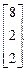
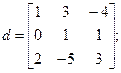 б)
б) 
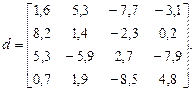
 б)
б) 

 б)
б) 

 и
и 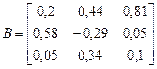
 =1,9;
=1,9;  =1,9;
=1,9;  =2,55; б)
=2,55; б)  =1,45;
=1,45;  =1,07;
=1,07;  =1,20.
=1,20.
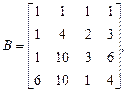

 б)
б) 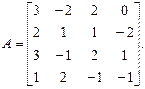
 б)
б) 




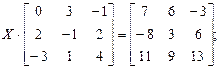 б)
б) 
 б)
б) 
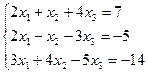 б)
б) 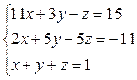
 =0,
=0,  =2; б) x =2, y = -2, z =1.
=2; б) x =2, y = -2, z =1. б)
б) 
 =-1; б)
=-1; б) 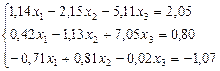 б)
б) 
 б)
б) 
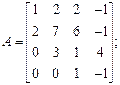 б)
б) 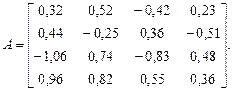
 б)
б) 
 б)
б) 
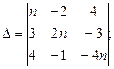


 ,
,  ,
,  и
и  :
: ,
,  ,
,  ,
,  .
. ;
; =2
=2  -
-  =3
=3