
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пусть дана квадратная матрицаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
порядка n. Квадратная матрица А-1 порядка n называется обратной для А, если АА-1=А-1А=Е. Матрица А называется невырожденной, если
Теорема. Матрица А имеет обратную тогда и только тогда, когда она невырожденная. Доказательство. Пусть Пусть теперь Покажем, что
Заметим, что здесь алгебраическое дополнение элементов i-ой строки матрицы Если
В силу свойства 7, 8 определителей (см.раздел 1)
Таким образом, С=Е. Аналогично доказывается, что ВА=Е т.е. В=А-1. Теорема доказана. Обратную матрицу для невырожденной матрицы А находят по формуле (2). Пример 7. Найти А-1, если
Решение.
По формуле (2)
Проверку сделайте самостоятельно.
Рассмотрим систему n линейных уравнений с n неизвестными
Обозначим
Тогда система (3) равносильна матричному уравнению – AX=B (4) Предположим теперь, что
т. е. Пример 8. Решить матричным способом систему уравнений
В нашем случае
т.е. x =1, y =0, z =-1. РАНГ МАТРИЦЫ. ИССЛЕДОВАНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Рассмотрим матрицу
размера m×n. Выберем в А произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, составляют квадратную матрицу k -го порядка, определитель которой называется минором k -го порядка матрицы А. Минорами 1-го порядка являются сами элементы матрицы А. Рангом матрицы А называется наивысший порядок отличных от нуля ее миноров. Ранг матрицы А будем обозначать r (А). Если все элементы А равны нулю, то полагаем r (A)=0. Можно обосновать следующее правило вычисления ранга матрицы: при вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор К-го порядка D, отличный от нуля, то требуют вычисления лишь миноры (k +1)-го порядка, окаймляющие минор D (т.е. содержащие его целиком внутри себя). Если они все равны нулю, то ранг матрицы равен k.
Пример 1. Вычислить ранг матрицы
Заметим, что в матрице А содержатся отличные от нуля миноры 2-го порядка, например,
Оба минора 3-го порядка, окаймляющие минор D, равны нулю:
Таким образом, Рассмотрим систему m линейных уравнений с n неизвестными:
Матрицы
называются соответственно матрицей системы и расширенной матрицей системы (I).
Теорема Кронекера-Капелли. Система линейных уравнений (I) совместна тогда и только тогда, когда r (A) = r (A*). Эту теорему мы доказывать не будем, но укажем, как практически отыскать все решения системы (I). Пусть r (A) = r (A*) = r, т.е. система (I) совместна. Если вычислять r (А) методом окаймляющих миноров, то в матрице А найдем минор r –го порядка D Оставляем в системе лишь те r уравнений, коэффициенты которых вошли в D. Получим систему (2). Оказывается, что каждое из отброшенных уравнений является суммой уравнений (2), умноженных на некоторые числа. Если r = n, то по теореме Крамера система (2) имеет единственное решение, которое находим, например, по формулам Крамера. Если же r < n, то в левых частях уравнений системы (2) оставляем те r неизвестных, коэффициенты при которых вошли в D. Остальные члены объявляем свободными и переносим в правые части уравнений. Придавая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных (например, по формулам Крамера), находим все (бесконечно много) решения системы (2). А значит, и системы (I). В частности справедливо предположение, что совместная система (I) тогда и только тогда обладает единственным решением, когда r (A) = n, т.е. ранг матрицы А равен числу неизвестных. Следствие. Система n линейных однородных уравнений с n неизвестными
тогда и только тогда имеет ненулевое значение, когда
Пример 2. Решить систему
Здесь
r (A) = 2 (пример 1),
Минор матрицы А*, окаймляющий D не входящий в А, равен 0.
Таким образом, r (A*) = 2 и система совместна. Коэффициенты 3-го уравнения не входят в минор D, поэтому 3-е уравнение можно отбросить (действительно, оно является суммой I-го и 2-го, умноженного на 5). Получим
Коэффициенты при х1 и х4 не входят в D, объявляем х1 и х4 свободными и переносим в правую часть:
По формулам Крамера
Эти равенства определяют общее решение заданной системы. Придавая в них свободным неизвестным х1, х4 произвольные числовые значения, получаем все решения нашей системы.
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ. СОБСТВЕННЫЕ ВЕКТОРЫ
Для простоты и наглядности ограничимся рассмотрением векторного пространства R2 или R3, т.е. совокупности векторов пространства или плоскости. Будем считать, что все векторы исходят из фиксированной точки O. Пусть задано отображение j пространства в себя, т.е. каждому вектору I) 2)
Пример I. Пусть a0 – фиксированное число. Полагаем 2. Поворот плоскости вокруг точки O на некоторый угол есть линейное преобразование пространства R2. 3. Пусть
то y - линейное преобразование и Зафиксируем в пространстве R3 некоторый базис
Матрица
называется матрицей линейного преобразования j в базе
Теорема 1. Пусть Bφ - матрица линейного преобразования j в базе w1, w2, w3. Тогда матрицы Аφ и Bφ подобны, т.е. найдется такая невырожденная матрица Т, что Bφ = T Аφ T-1, Аφ = T-1 Bφ T. Если Y – линейное преобразование, для которого Опускаем доказательство, которое можно провести прямым вычислением. Если l - некоторое неизвестное, Е – единичная матрица 3-го порядка, то многочлен 3-й степени
называется характеристическим многочленом преобразования j (матрицы Аφ), уравнение
Теорема 2. Подобные матрицы обладают одинаковыми характеристическими многочленами, а значит, и одинаковыми характеристическими корнями. Доказательство. Пусть A = T-1BT. Тогда
В этой цепочке равенств второе следует из того, что lЕ перестановочна с любой матрицей, третье получается в силу закона дистрибутивности, четвертое равенство выполняется, так как определитель произведения матриц равен произведению определителей этих матриц, а последнее равенство вытекает из соотношения
Определение. Ненулевой вектор Считаем, что собственный вектор В примере 1 каждый ненулевой вектор является собственным, а в примере 2, если угол поворота не является кратным p, линейное преобразование не имеет собственных векторов. Рассмотрим линейное преобразование j с матрицей (I) в базе
Тогда
Из формулы (2), приравнивая координаты, получаем b1a11 + b2a21 + b3a31=l0b1, b1a12 + b2a22 + b3a32=l0b2, b1a13 + b2a23 + b3a33=l0b1. Так как a ¹ 0, то b1, b2, b3 – ненулевое решение однородной системы
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 637; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


 .
.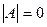 . Предположим, что матрица А имеет обратную. Тогда ввиду (1) получаем, что
. Предположим, что матрица А имеет обратную. Тогда ввиду (1) получаем, что  . Противоречие.
. Противоречие. - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  в
в  .
. (2)
(2) составляет i-й столбец.
составляет i-й столбец. , то
, то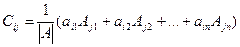




 (3)
(3) .
. , а значит, по теореме существует матрица A-1. Используя ассоциативность умножения матриц, легко решить матричное уравнение (4). Умножим обе части этого уравнения слева на A-1:
, а значит, по теореме существует матрица A-1. Используя ассоциативность умножения матриц, легко решить матричное уравнение (4). Умножим обе части этого уравнения слева на A-1:
 .
.

 найдена в примере 7 данного раздела. Итак,
найдена в примере 7 данного раздела. Итак,

 .
. .
. ,
, 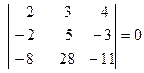 .
.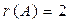 .
. (I)
(I) ,
, 
 0.
0.
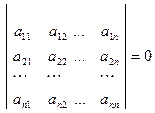 .
.
 ,
,  ,
, .
.


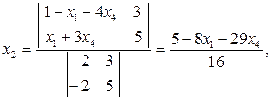

 пространства сопоставлен вектор
пространства сопоставлен вектор  этого же пространства. Отображение j называется линейным преобразованием, если для любых векторов
этого же пространства. Отображение j называется линейным преобразованием, если для любых векторов  пространства и любого числа a выполняются равенства:
пространства и любого числа a выполняются равенства: ,
, .
. для любого вектора а пространства. Легко проверить, что j - линейное преобразование.
для любого вектора а пространства. Легко проверить, что j - линейное преобразование. – база (базис) R3. Если
– база (базис) R3. Если  . Пусть j - линейное преобразование R3. Тогда в силу равенств I), 2)
. Пусть j - линейное преобразование R3. Тогда в силу равенств I), 2)  . Поэтому достаточно знать действия на элементах базы. Возникает вопрос, существует ли такое линейное преобразование y, которое базисные элементы
. Поэтому достаточно знать действия на элементах базы. Возникает вопрос, существует ли такое линейное преобразование y, которое базисные элементы  . Ответ положительный. Если положить
. Ответ положительный. Если положить .
. = с1,
= с1,  = с2,
= с2,  = с3. (Проверьте!)
= с3. (Проверьте!) по базе
по базе  = a11ℓ1 + a12ℓ2 + a13ℓ3,
= a11ℓ1 + a12ℓ2 + a13ℓ3,
 = a21ℓ1 + a22ℓ2 + a23ℓ3,
= a21ℓ1 + a22ℓ2 + a23ℓ3, = a31ℓ1 + a32ℓ2 + a33ℓ3.
= a31ℓ1 + a32ℓ2 + a33ℓ3. (I)
(I)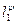 = ω1,
= ω1,  =ω2,
=ω2,  = ω3, то в качестве матрицы Т можно взять матрицу преобразования Y в базе
= ω3, то в качестве матрицы Т можно взять матрицу преобразования Y в базе 
 - называется характеристическим уравнением преобразования j (матрицы Аφ), а корни этого уравнения – характеристическими корнями преобразования j (матрицы Аφ).
- называется характеристическим уравнением преобразования j (матрицы Аφ), а корни этого уравнения – характеристическими корнями преобразования j (матрицы Аφ).
 .
. аj = l0
аj = l0  – собственный вектор для любого a ¹ 0. Действительно,
– собственный вектор для любого a ¹ 0. Действительно,  =
=  =
=  =
=  .
. является собственным вектором преобразования j.
является собственным вектором преобразования j. (2)
(2)
 .
. (3)
(3)


