
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определитель квадратной матрицы и его геометрический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определитель квадратной матрицы и его геометрический смысл.
Определитель – каждой квадратной матрице А ставится в соответствие число, которое называется определителем матрицы и обозначают det(A).
1. Если А=[C], то det(A)=C 2. Если А= Mik – минор элемента aik. Минор – определитель матрицы, который получается после вычеркивания или удаления из матрицы А i-й строки k-го столбца. i, k Это рекуррентное определение. Мы не сразу получаем определитель матрицы 3-го порядка, а по данной формуле приходим к вычислению 3-х определителей 2-го порядка и т.д.
Геометрический смысл определителей. Пусть Любой вектор можно линейно разложить в этом базисе. Пусть
Знак определителя определяют ориентацию векторов в пространстве. Это геометрический смысл определителя 3-го порядка в 3-х мерном пространстве. На плоскости остается 2 базисных вектора.
Это геометрический смысл определителя 2-го порядка на двухмерном пространстве. Переводим в n-мерное пространство Rn. В этом пространстве стандартный базис:
V=|det(A)| -- определитель объема тела, построенного на данных векторах.
Вычисление определителей Определитель – каждой квадратной матрице А ставится в соответствие число, которое называется определителем матрицы и обозначают det(A). 1. Если А=[C], то det(A)=C 2. Если А= Mik – минор элемента aik. Минор – определитель матрицы, который получается после вычеркивания или удаления из матрицы А i-й строки k-го столбца. i, k Это рекуррентное определение. Мы не сразу получаем определитель матрицы 3-го порядка, а по данной формуле приходим к вычислению 3-х определителей 2-го порядка и т.д.
Вычисление определителя 2-го порядка:
Это следует из Опр. 1.
Выведем для определителя 3-го порядка правило треугольника.
Прим.: det(12)=12
Определитель квадратной матрицы и его геометрический смысл.
Определитель – каждой квадратной матрице А ставится в соответствие число, которое называется определителем матрицы и обозначают det(A).
1. Если А=[C], то det(A)=C 2. Если А= Mik – минор элемента aik. Минор – определитель матрицы, который получается после вычеркивания или удаления из матрицы А i-й строки k-го столбца. i, k Это рекуррентное определение. Мы не сразу получаем определитель матрицы 3-го порядка, а по данной формуле приходим к вычислению 3-х определителей 2-го порядка и т.д.
Геометрический смысл определителей. Пусть Любой вектор можно линейно разложить в этом базисе. Пусть
Знак определителя определяют ориентацию векторов в пространстве. Это геометрический смысл определителя 3-го порядка в 3-х мерном пространстве. На плоскости остается 2 базисных вектора.
Это геометрический смысл определителя 2-го порядка на двухмерном пространстве. Переводим в n-мерное пространство Rn. В этом пространстве стандартный базис:
V=|det(A)| -- определитель объема тела, построенного на данных векторах.
Вычисление определителей Определитель – каждой квадратной матрице А ставится в соответствие число, которое называется определителем матрицы и обозначают det(A). 1. Если А=[C], то det(A)=C 2. Если А= Mik – минор элемента aik. Минор – определитель матрицы, который получается после вычеркивания или удаления из матрицы А i-й строки k-го столбца. i, k Это рекуррентное определение. Мы не сразу получаем определитель матрицы 3-го порядка, а по данной формуле приходим к вычислению 3-х определителей 2-го порядка и т.д.
Вычисление определителя 2-го порядка:
Это следует из Опр. 1.
Выведем для определителя 3-го порядка правило треугольника.
Прим.: det(12)=12
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 809; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.008 с.) |

 , то det(A)=
, то det(A)=  -- разложение определителя по 1-й строке. Aik=(-1)i+k*Mik – алгебраическое дополнение элемента aik.
-- разложение определителя по 1-й строке. Aik=(-1)i+k*Mik – алгебраическое дополнение элемента aik. .
. -- стандартные наги.
-- стандартные наги.  .
.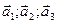 -- произв. сист. вект. в пространстве.
-- произв. сист. вект. в пространстве.  . Из координат этих векторов составим матрицу:
. Из координат этих векторов составим матрицу: Тогда определитель этой матрицы равен ±V, где V – объем параллелепипеда, состоящего из этих векторов. det(A)= ±V.
Тогда определитель этой матрицы равен ±V, где V – объем параллелепипеда, состоящего из этих векторов. det(A)= ±V. и
и  (произвольные вектора). Составим матрицу:
(произвольные вектора). Составим матрицу: Тогда det(A)=±S, где S – площадь параллелограмма, построенного на этих векторах.
Тогда det(A)=±S, где S – площадь параллелограмма, построенного на этих векторах. .
.  , где единица стоит на k-м месте. Выбираем произвольные вектора
, где единица стоит на k-м месте. Выбираем произвольные вектора  . Составляем матрицу из этих векторов:
. Составляем матрицу из этих векторов: Теперь можно обобщить понятие объема, образованного этими векторами в этом пространстве.
Теперь можно обобщить понятие объема, образованного этими векторами в этом пространстве. =a11*a22-a12*a21
=a11*a22-a12*a21 =a11*A11+a12*A12=a11(-1)1+1*a22+a12(-1)1+2*a21=a11*a22-a12*a21
=a11*A11+a12*A12=a11(-1)1+1*a22+a12(-1)1+2*a21=a11*a22-a12*a21 =(a11*a22*a33+a12*a23*a31+a21*a32*a13)-(a31*a22*a13+a23*a32*a11+a12*a21*a33). Справа в первой скобке сумма произведений элементов, которые образуют треугольник со стороной параллельной главной диагонали. Во второй скобке – сумма произведений элементов, которые образуют треугольник со стороной параллельной побочной диагонали.
=(a11*a22*a33+a12*a23*a31+a21*a32*a13)-(a31*a22*a13+a23*a32*a11+a12*a21*a33). Справа в первой скобке сумма произведений элементов, которые образуют треугольник со стороной параллельной главной диагонали. Во второй скобке – сумма произведений элементов, которые образуют треугольник со стороной параллельной побочной диагонали. =1*6-2*5=-4
=1*6-2*5=-4 =5*
=5*  -0+0=5*(8-6)=10 (разложение по 3-й строке)
-0+0=5*(8-6)=10 (разложение по 3-й строке) =3*
=3*  (разложение по 3-му столбцу)
(разложение по 3-му столбцу) Если выше главной диагонали или ниже главной диагонали все нули, то определитель равен произведению элементов на главной диагонали.
Если выше главной диагонали или ниже главной диагонали все нули, то определитель равен произведению элементов на главной диагонали.


