
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители, свойства, вычисление.Содержание книги Поиск на нашем сайте
Определители, свойства, вычисление. Определитель (детерминант), матрица (А) = Обозн: ▲, IAI, D. Определ-ль 3го порядка.
1)Существует удобная схема для вычисления определителя третьего порядка:
2)правило Саррюса: Дописывание двух первых строк или столбцов.
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33. 3) разложение по строке:
Определ-ль n-го порядка им n строк и n столбцов.
Свойства определителей: 1) если у опред-ля произвольная строка (столбец) состоит только из нулей, то опред-ль =0; 2) если производные 2 строки (столбца) опред-ля пропорциональны, то опред-ль = 0; 3) если произ строку (столбец) опред-ля умножить на производное число, то и весь опред-ль умн-ся на это число; 4) если 2 строки (столбца) опред-ля поменять местами, то опред-ль изменит знак; 5) если к произв строке (столбцу) опред-ля прибавить любую другую строку (столбец), умноженную на проиводн число, то опр-ль не изм-ся; 6) опред-ль произведение матриц = произведению их опред-лей. Матрица, опред-ль котор =0,назыв вырожденной; опред-ль котор Матрицы. Виды матриц. Действия над матрицами. Вычисление обратной матрицы. Ранг и его вычисление. Матрица - А= Числа aijназыв эл-тами матрицы А. Элементы, стоящие на диаг-ли, идущ из левого верхн угла, образ главнуюd. Матрицы равны м/усобой, если все соотв-щие эл-ты этих матриц=. А=В, aij=bij. Матрица, у котор число строк =числу столбцов, назыв квадратной. Квадратная матрица, у котор все эл-ты, кроме эл-товглd, =0, назыв диагональной. Диагональная матрица, у которкажд эл-т глd=1, назыв единичной. Квадратная матрица назыв треуг-ной, если все эл-ты, располож по одну сторону от глd, =0. Матрица, все эл-ты котор =0,назыв нулевой. Матрица, содержащая 1 столбец или строку, назыв вектором. Матрицаполуч из данной заменен производной ее строки столбцом с тем же №, назыв транспонированной. Пример: А= Св-во: ( Действия над матрицами. 1) суммой матриц А и В одинакового размера назыв М. С того же размера, причем сij=aij+bij. 1.коммуникативность:.А+В=В+А. 2.ассоциативность: (А+В)+С=А+(В+С)=А+В+С. 2) произведением М. А на число λназыв М. В того же размера, что и М. А, причем эл-ты М. bij=λaij,Ɏλ, Ɏij. 1.λ(µА)=(λµ)А (ассоц-ть) 2.λ(А+В)=λА+λВ (дистрибутимость) 3.(λ+µ)А=λА+µА. 3) линейной комбинацией матриц А и В одного размера назыв выражение вида αА+βА, где α и β –любые числа. 4) произвед-ем м-ц А и В р-ров (мхn и nxr) назыв М. С такая что Сij=ai1*b1j+ai2*b2j+…aik*bkj+…+ain*bnj
Элементарные преобразования. 1)перемена местами 2х строк(столбцов) 2)умножение строки(столбца) на число, отлично от 0. 3)прибавление к элементам одной строки (столбца) соотв эл др строки(столбца). Матрица Вназыв э квивалентной М.А. В Обратная матрица. Обр м-ца Если опред-ль =0, то квадр м-ца не им обратной и назыв вырожденной. Если опред-ль ≠0, то обр м-ца не им обратной Схема нахождения обр. мат-цы: 1) вычисляем опред-ль М.А, опред-ль≠0 2) находим м алгебр-ких дополнений Аij 3) транспонир-ть м.Aij и получить 4) находим м по формуле: 5) проверка: Ранг матрицы. Минором некоторого эл-та aijопред-ляn-го порядка назывопредел-ль (n-1) порядка, которполуч из исходного путем вычеркивания строки и столбца, на пересечение которых находится выбран эл-т Mij – минор для эл.
Опред-ние Алгебраич дополнением будет назыв-сяпроизв-ние Наиб из порядков миноров данной м-цы, отличных от 0, назыв рангом м-цы. Обозн: r, r(A), rang (A) Минор, порядок которопредел-ет ранг м-цы, назыв базисным. Решение с.л.а.у.
i= 4. С.л.а.у. с квадратичными матрицами и методы их решения (метод Крамера, Гаусса, матричный способ) Метод Крамера. Пусть данасис-маn-лин уравнений с nнеизв-ми. AX=B, B 1) 2)
3)
4)Проверка. Метод обратной матрицы. М.обр м-цы применяют как метод, если число уравнений = числу неизвестных.
B= A* E*X= Cхема решения: 1) вычислить
Метод Гаусса. -метод последоват. исключения переменных. Этот м-д состоит в том, что при помощи эл-ных преобразований (умн-нияуравн на число≠0, перестановка уравнений, прибавл-иеур-ния к др-му, умнож-му на число) искл-ся переменные. Сис-маназыв совместной, если она им хотя бы 1 реш. Назыв несовместной, если не им решений.
Выводы:1-ое уравнение в мет гаусса оставл, а из остальн исключаем неизвестные. 1-ое и 2-ое оставляем, а из ост иключ неизвестные и т.д. Если получим уравнение вида 0=а, то система назывнесовместной и не им решений. Если получили уравн вида 0=0, то система имеет бесконечное множество решений. Проекции вектора на ось. Ось – прямая, им направление. Числов ось – прямая, с нач отсчета и единичным масштабом. Проекции сущ 2 вида: геометр-кая и алгебр-кая. Проекция вектора на ось равна произведению длины вектора
При умножении вектора на число его проекция на ось также умножается на это число. Проекция суммы векторов на ось равна сумме проекций слагаемых:
Свойства проекций:1) пр Проекция в-ра на ось положит-на (отриц-на), если век-р образует с осью острый (тупой) угол и равна 0, если этот угол прямой. Проекции равн век-ров равны м/у собой. 2) проекция суммы неск век-ров на одну и ту же ось = сумме их проекций на эту ось. 3) при умножении
Квадратичные формы. Определение: Однородный многочлен второй степени относительно переменных х1 и х2 Ф(х1, х2) = а 11 не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1 и х2. Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3. Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А = Пусть на плоскости задан ортогональный базис Если задана квадратичная форма Ф(х1, х2) = а 11 Приведение квадратичных форм к каноническому виду. Рассмотрим некоторое линейное преобразование А с матрицей Это симметрическое преобразование можно записать в виде: y1 = a11x1 + a12x2 y2 = a12x1 + a22x2 где у1 и у2 – координаты вектора Очевидно, что квадратичная форма может быть записана в виде Ф(х1, х2) = х1у1 + х2у2. Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 их2 – скалярное произведение Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду. Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:
При переходе к новому базису от переменных х1 и х2 мы переходим к переменным
Тогда
Выражение Полярная система координат. Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки). Полярными координатами произвольной точки М (относительно заданной системы) называются числа
Символ М( Полярный угол В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом, 2). При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу - вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки). При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам
В этом же случае формулы
являются формулами перехода от декартовых координат к полярным. При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми. Прямая на плоскости. Прямая на плоскости и плоскость в пространстве обладают тем общим свойством, что дополнительная размерность равна единице. Другими словами, что все нормальные векторы к плоскости являются коллинеарными и все нормальные векторы к прямой на плоскости тоже коллинеарны. Отметим, что прямая в пространстве этим свойством не обладает. Нормальные векторы к ней, если их начала поместить в одну точку, "заполняют" целую плоскость. Так как формулы (11.1), (11.3), (11.4), (11.5), (11.6), (11.7) основывались на нормальном векторе к плоскости, то они остаются верными и для прямой на плоскости, если из них исключить третью координату. Доказательство этих формул для прямой на плоскости полностью повторяет их доказательство для плоскости в пространстве.
если прямая имеет уравнение Кроме перечисленных выше формул для прямой на плоскости стоит отметить еще одну, связанную с тем, что на плоскости чаще всего используется уравнение прямой с угловым коэффициентом Предложение 11.2 Пусть заданы две прямые
Если Доказательство. Как известно из школьного курса математики, угловой коэффициент в уравнении прямой
Рис.11.10.Угол между прямыми Так как
что дает формулу (11.10). Если же
Следовательно, 18. Расстояние от точки до прямой. Угол между прямыми. Условия параллельности и перпендикулярности прямых. Рас-ние от точки до прямой. Пусть даны точка М(Х0; У0) и прямая Ax+By+c=0. Под рас-нием от М до прямой АВ понимается длина перпендик-раd=MN, опущенного из т.М на прямую АВ. Для опред-ния расстояния d нужно: а) составить уравнение прямой MN,перендик-ной данной и проходящий ч/з т. М0(Х0;У0); б) найти т N(x1;y1)пересеч-ния прямых, ршивсис-мууравн этих прямых; в) по формуле Находим d=MN. В рез-те получим: Угол между прямыми. Пусть заданы 2 прям И треб-ся определить угол Тогда
Окружность. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Получим уравнение окружности, если известны ее центр и радиус. Окружность радиуса Rс центром в т.
Эллипс. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная. Пусть F1и F2 – фокусы эллипса. Начало O системы координат расположим на середине отрезка F1F2. Ось Ox направим вдоль этого отрезка, ось Oy – перпендикулярно к этому отрезку. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами – 2c. Тогда в выбранной системе координат эллипс имеет уравнение
Прямоуг-ник со стор 2а и 2в назыв-ся основным прямоуг-ником гиперболы.
Равносторонней гиперболой назыв такую гиперболу, где ее полуоси равны a=b.
Парабола. Мн-во точек, кажд из котор одинаково удалена от данной точки, назыв фокусом и данной прямой, назыв директрисой. Расст-ние от фокуса F до директрисы назыв параметром(р>0).
FM- фокальный радиус т-ки М. О(0;0) – вершина параболы. Т-ма: Уравнение определ либо окр-ть (А=С), эллипс (А*С>0), гиперболу (А*С<0), параболу(А*С=0). Возможный случай вырождения: для эллипса(окр-ти)-в точку или мнимый эллипс(окр-ть); для гиперболы – в пару пересек-сяпрямых; для параболы-в пар парал-ных прямых. Определители, свойства, вычисление. Определитель (детерминант), матрица (А) = Обозн: ▲, IAI, D. Определ-ль 3го порядка.
1)Существует удобная схема для вычисления определителя третьего порядка:
2)правило Саррюса: Дописывание двух первых строк или столбцов.
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33. 3) разложение по строке:
Определ-ль n-го порядка им n строк и n столбцов.
Свойства определителей: 1) если у опред-ля произвольная строка (столбец) состоит только из нулей, то опред-ль =0; 2) если производные 2 строки (столбца) опред-ля пропорциональны, то опред-ль = 0; 3) если произ строку (столбец) опред-ля умножить на производное число, то и весь опред-ль умн-ся на это число; 4) если 2 строки (столбца) опред-ля поменять местами, то опред-ль изменит знак; 5) если к произв строке (столбцу) опред-ля прибавить любую другую строку (столбец), умноженную на проиводн число, то опр-ль не изм-ся; 6) опред-ль произведение матриц = произведению их опред-лей. Матрица, опред-ль котор =0,назыв вырожденной; опред-ль котор
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.015 с.) |

 =a1b2-a2b1, называется число равное разности произведений элементов, лежащих на главной и побочной диагоналях.
=a1b2-a2b1, называется число равное разности произведений элементов, лежащих на главной и побочной диагоналях. =
=  +
+  +
+ 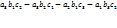



 ,
,  ,
, 

 0,назыв невырожденной.
0,назыв невырожденной. -ная табл чисел, содержащая m-строк и n-столбцов.
-ная табл чисел, содержащая m-строк и n-столбцов. , A =(aij), i=1,2,3…m- № строки, j=1,2,3…, j - № столбца.
, A =(aij), i=1,2,3…m- № строки, j=1,2,3…, j - № столбца.
 ,
,  .
. .
. -такая м-ца, котор в произв с данной м-цей А дает единицу и наоборот. А*
-такая м-ца, котор в произв с данной м-цей А дает единицу и наоборот. А*  , Aij-м-ца алгебр дополнений, соотв эл-тов М.А.
, Aij-м-ца алгебр дополнений, соотв эл-тов М.А. , М22=
, М22=  , М13=
, М13=  , M23=
, M23=  .
. i-№ строки, j-№ столбца.
i-№ строки, j-№ столбца.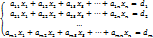
 переменные
переменные коэффициенты
коэффициенты , j=
, j=  - свободный член.
- свободный член. . Основная м-ца такой сис-мы – квадратная. Определ-ль этой м-цы
. Основная м-ца такой сис-мы – квадратная. Определ-ль этой м-цы  назыв-ся определителем этой системы.
назыв-ся определителем этой системы.
 ,
,  …
…
 ;
;  ;
; 

 , А=
, А=  , X=
, X= 
 , A*X=B
, A*X=B  *
* 
 X=
X=  ≠0; 2)
≠0; 2) 
 ; 4) проверка.
; 4) проверка.

 . Проверка.
. Проверка. на косинус угла между вектором и осью:
на косинус угла между вектором и осью:


 на l = произв
на l = произв  на cos
на cos  м/у вектором и осью.
м/у вектором и осью. 
 его проекция на ось также умнож-ся на это число:
его проекция на ось также умнож-ся на это число: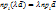 .
.

 . Определитель этой матрицы называется определителем квадратичной формы.
. Определитель этой матрицы называется определителем квадратичной формы. . Каждая точка плоскости имеет в этом базисе координаты х1, х2.
. Каждая точка плоскости имеет в этом базисе координаты х1, х2. .
. в базисе
в базисе  .
.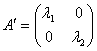 .
. и
и  . Тогда:
. Тогда:
 .
. называется каноническим видом квадратичной формы.
называется каноническим видом квадратичной формы. и
и  (см. рис.). Угол
(см. рис.). Угол  при этом следует понимать так, как принято в тригонометрии. Число
при этом следует понимать так, как принято в тригонометрии. Число  называется первой координатой, или полярным углом точки М (
называется первой координатой, или полярным углом точки М (
 , где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам
, где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам 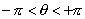 , называется главным.
, называется главным. ,
,  .
. ,
, 
 11.1
11.1 11.3
11.3 11.4
условие перпендикулярности плоскостей:
11.4
условие перпендикулярности плоскостей:
 11.5
условие параллельности плоскостей
11.5
условие параллельности плоскостей
 11.6
расстояние
11.6
расстояние  от точки
от точки  до плоскости
до плоскости  определяется по формуле
определяется по формуле
 11.7
11.7
 , то расстояние от точки
, то расстояние от точки  до этой прямой получается из формулы
до этой прямой получается из формулы 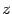 :
: 
 , хорошо известное по школьному курсу математики.
, хорошо известное по школьному курсу математики. и
и  , (
, ( ). Тогда, если
). Тогда, если  , то угол
, то угол  между этими прямыми можно найти из формулы
между этими прямыми можно найти из формулы
 , то прямые перпендикулярны.
, то прямые перпендикулярны.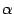 наклона прямой к оси
наклона прямой к оси  . Из рис. 11.10 видно, что
. Из рис. 11.10 видно, что  .
.
 ,
,  , то при
, то при 
 , откуда
, откуда
 и
и  .
.


 причем
причем  ,
,  ,
,  ,
, 
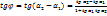
 имеет уравнение
имеет уравнение
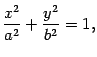 где
где  Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси Ox и Oy, начало координат -- центр симметрии.
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии -- центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины -- большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины -- малой полуосью. Величина
Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси Ox и Oy, начало координат -- центр симметрии.
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии -- центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины -- большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины -- малой полуосью. Величина  называется эксцентриситетом эллипса.
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (-a;0), (a;0),(0;-b),(0;b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины b, а именно,
называется эксцентриситетом эллипса.
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (-a;0), (a;0),(0;-b),(0;b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины b, а именно,  .
Эксцентриситет E эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<E<1.
F1M=r1, F2M=r2 –фокальные радиусы.
r1+r2=2a. r1=a+Ex; r2=a-Ex.
X=
.
Эксцентриситет E эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<E<1.
F1M=r1, F2M=r2 –фокальные радиусы.
r1+r2=2a. r1=a+Ex; r2=a-Ex.
X=  – прямые директрисы.
– прямые директрисы.
 -основное ур-ние эллипса.
-основное ур-ние эллипса.
 .
Гипербола.
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Пусть расстояние между фокусами F1и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение
.
Гипербола.
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Пусть расстояние между фокусами F1и F2 гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение
 где
где  ,где а – действит полуось, в – мнимая пол-сь.
,где а – действит полуось, в – мнимая пол-сь.

 - асимптоты.
- асимптоты.
 ;
; 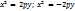 .
.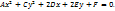 - общурлин 2го порядка.
- общурлин 2го порядка.


