Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов. Свойства. Применение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скалярным произведением векторов
Если векторы заданы в координатной форме то их скалярное произведение вычисляется по формуле:
Свойства скалярного произведения: 1) 2) 3) 4) 5) Векторное произведение векторов. Свойства. Применение. Векторным произведением векторов 1) 2) вектор 3) Обозначается:
Свойства векторного произведения векторов 1) 2)
4) 5) Если заданы векторы
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах Замечание: если требуется вычесть площадь параллелограмма, то нужно посчитать сначала затем Смешанное произведение векторов. Свойства. Применение. Смешанным произведением трех векторов
Смешанное произведение обладает следующими свойствами: 1) 2)
4) объем параллелепипеда, построенного на векторах если a*b*c>0, то тройка a,b,c – правая, если a*b*c<0, то тройка a,b,c - левая
Замечание Условие компланарности 3х векторов.
Векторный базис. Координаты вектора. Разложение вектора по базису. Базис – группа в-в ч/з котор выражают все лин пространство. В 3хмерном простр-ве базис состоит из 3х некомплан-ныхв-в. В пл-ти 2 в-ра. Ортогональный базис состоит из взаимноперпендик-ныхв-в. ( Нормированный базис состоит из единичных век-ров( По умолчанию берут ортогональный базис.
Разложение по базису:
13.Условия коллинеарности, ортогональности, компланарности векторов. Условие ортогональности векторов Два вектора Условие коллинеарности векторов Если векторы Условие компланарности векторов Векторы Линейные операторы. Собственные значения и собственные векторы линейного оператора. Линейные модели обмена.
Собственные векторы и собственные значения линейного оператора. 1) Матрица линейного оператора: 4) Ядро линейного оператора: Пусть φ - Л.О. векторного пространства V над полем P и Характеристическое уравнение Л.О. φ: Множество собственных векторов, отвечающих собственному значению λ:
Л.О. вектороного пространства называются Л.О. с простым спектром, если φ, если φ имеет ровно n собственных значений. Если φ - Л.О. с простым спектром, то он имеет базис из собственных векторов, относительно которого матрица Л.О. φ диагональна.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.166 (0.007 с.) |

 и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.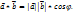
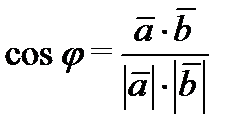
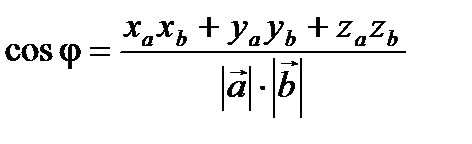
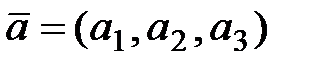 ,
, 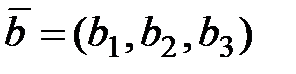 ,
,

 =0
=0
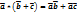
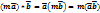
 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: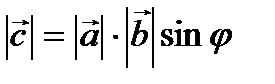 , где j - угол между векторами
, где j - угол между векторами 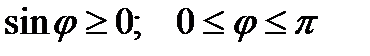
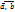 , и
, и 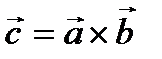 или
или  .
.
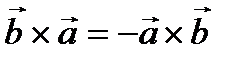 ;
; =0
=0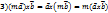
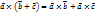
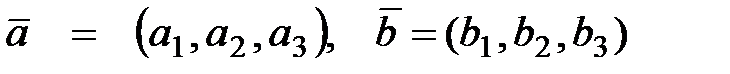 в декартовой прямоугольной системе координат с единичными векторами
в декартовой прямоугольной системе координат с единичными векторами 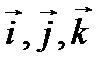 , то
, то
 -орты осей координат Ox, Oy, Oz, соответственно:
-орты осей координат Ox, Oy, Oz, соответственно: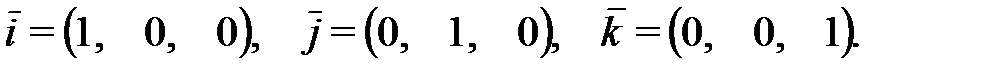
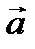 и
и  :
: 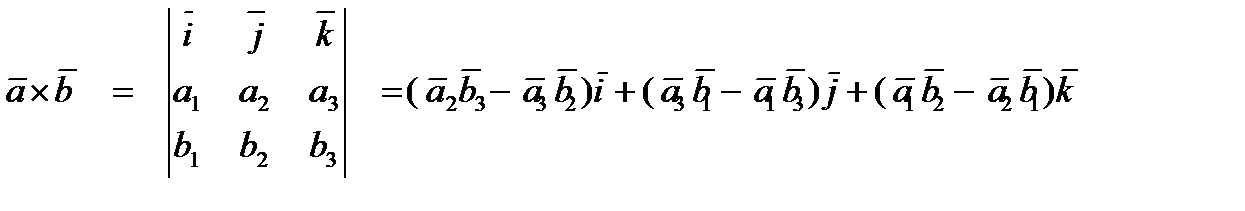 ,
,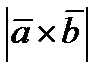 =
= 
 называется число
называется число 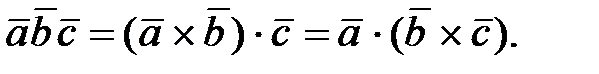
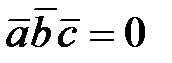 , если все три вектора параллельны одной и той же плоскости (компланарны);
, если все три вектора параллельны одной и той же плоскости (компланарны); циклическая перестановка
циклическая перестановка
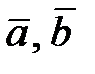 и
и  , равен
, равен 

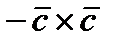 =0
=0
 =0.
=0. =>
=> 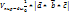
 )
)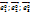 ).
).
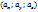 -проекции или коорд в-ра
-проекции или коорд в-ра  ортогональны при условии равенства нулю их скалярного произведения:
ортогональны при условии равенства нулю их скалярного произведения: 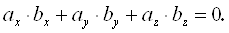
 коллинеарны (лежат на одной прямой или напараллельных прямых) т.е. угол между ними или 0, или 1800, то их векторное произведение равно нулю:
коллинеарны (лежат на одной прямой или напараллельных прямых) т.е. угол между ними или 0, или 1800, то их векторное произведение равно нулю: 
 компланарны (расположены в одной плоскости), если их смешанное произведение равно нулю:
компланарны (расположены в одной плоскости), если их смешанное произведение равно нулю: 
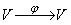 над полем P, есть линейный оператор, если
над полем P, есть линейный оператор, если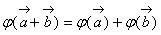 для любых векторов
для любых векторов 
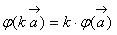 для любого вектора
для любого вектора 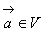 и любого
и любого  .
.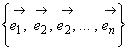
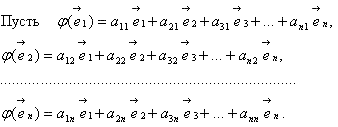

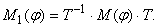

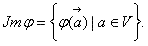
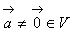 и
и 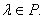
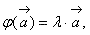 то λ - собственное значение
то λ - собственное значение - собственный вектор Л.О. φ, отвечающий λ.
- собственный вектор Л.О. φ, отвечающий λ.