
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скалярного произведения. Свойства скалярного произведенияСодержание книги
Поиск на нашем сайте
Умножение вектора на число Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число: Пример: A=(1,2,3); λ=2; A*λ=(1*2,2*2,3*2)=(2,4,6) Сложение векторов Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются: Свойства линейных операций: § А + В = В + А § (А + В) + С = А+(В + С) § λ(А + В) = λА + λВ § (λ+ μ)А = λА + μ А § λ(μ А) = (λμ)А Пример:
Определение скалярного произведения. Свойства скалярного произведения Скалярное произведение векторов Скалярным произведением векторов
Свойства произведения: § § § λ(A*B)=λ*A*B Пример:
Неравенство Коши-Буняковского. Неравенство треугольника (док-во) Угол между n-мерными векторам. Теорема о равенстве векторов Угол между векторами
Теорема: Ненулевые n-мерные вектора |A| и |B| равны, когда угол φ между ними равен 0 и |A| и |B| совпадают. Док-во: A=B (*A)=> AA=AB => AA=BB => √(AA)=√(BB) => |A|=|B| A=B => AA/|A||A| => A²/ |A|²=1 => φ=0
Коллинеарные вектора A и B коллинеарны, если AˆB=0 или AˆB=π; а) если AˆB=0, одинаково направленные вектора; б) если AˆB=π, противоположно-направленные вектора. Теорема: Ненулевые вектора A и B коллинеарны, когда можно подобрать такое число K, чтобы B=KA.
Разложение вектора по системе векторов. Свойства разложения
Говорят, что вектор B линейно выражается через вектора A1,A2…Ak, если вектор B равен некоторой линейной комбинации векторов A1,A2…Ak, т.е. существует набор чисел такой, что B=L1A1+L2A2+…+LkAk. L1,L2…Lk - коэффициент разложения вектора B по системе векторов A1,A2…Ak. Ненулевой вектор θ разлагается по любой системе векторов. Если вектор B разлагается по части системы векторов, то он разлагается по всей системе векторов. Каждый n-мерный вектор B=(b1,b1…bn) разлагается по диагональной системе n-мерных векторов с коэффициентами, равными координатам вектора B.
7) Элементарные преобразования системы векторов
Система векторов {A1,…Am,B}. Запись в виде матрицы, столбцы которой совпадают с координатами векторов: A1 A2 … Am | B a1 a2 … am | b1 ……………. | … an an … anm | bn a) вычеркивание из матрицы нулевой строки
b) умножение j-ой координаты векторов на числа, отличное от 0 c) прибавление к j-ой строки i-ой строки, умноженной на любое число
Подобные системы векторов Если систему векторов A1,A2…Am можно при помощи конечного числа элементарых преобразований превратить в систему B1,B2…Bm Подобные системы векторов всегда содержат одно и то же число векторов; размерности векторов в этих системах могут не совпадать.
Свойства: 1) Если A1,…Am подобна B1,…Bm, то B1,…Bm подобна A1,…Am 2) Если система А подобна системе В, а система В подобна системе С, то система А подобна системе С 3) Пусть система А подобна системе В. Если нулевой вектор разлагается по системе векторов А, то он разлагается по системе векторов В с теми же коэффициентами. Линейная зависимость систем векторов A1,A2…Am линейна зависима, если имеется 2 различных разложения нулевого вектора по системе векторов A1,…Am
Теорема о разложении вектора по линейно независимой системе векторов. Теорема об условии равносильности линейно зависимой системы векторов. Теорема: Дана система А, тогда след. условие равносильно: А) система А линейно зависима/ линейно не зависима Б) есть ненулевое разложение нулевого вектора по системе А/ есть только нулевое разложение нулевого вектора по системе А В) хотя бы один из векторов системы А разлагается по остальным/ ни один из векторов системы А не разлагается по остальным векторам этой системы. Базис и ранг системы векторов
Базисом системы векторов называется такая её часть, которая удовлетворяет следующим её условиям: а) B1,B2,…Br линейно не зависимы б) каждый вектор системы A1,…Am разлагается по векторам B1,…Br
Рангом системы векторов называется число векторов в любом её базисе
Умножение матрицы на вектор, на матрицу. Свойства
Операция определена, когда координаты вектора столько, сколько же и матрицы. An * Bn k = Ck
Свойства: a) (K+L)A=KA+LA; K,L-векторы, A-матрица b) (kL)A=k(LA); k-число c) (LA)K=L(AK); K,L-векторы
Теорема Крамера Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*. Очевидно, что система (1) может быть записана в виде: x1 + x2 + … + xn Доказательство. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
x1 = D1/D = 1; x2 = D2/D = 2; Умножение вектора на число Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число: Пример: A=(1,2,3); λ=2; A*λ=(1*2,2*2,3*2)=(2,4,6) Сложение векторов Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются: Свойства линейных операций: § А + В = В + А § (А + В) + С = А+(В + С) § λ(А + В) = λА + λВ § (λ+ μ)А = λА + μ А § λ(μ А) = (λμ)А Пример:
Определение скалярного произведения. Свойства скалярного произведения
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.103 (0.01 с.) |



 и
и 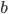 называется величина, вычисляемая по формуле:
называется величина, вычисляемая по формуле:



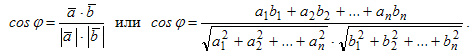


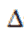 =
=  = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.


