Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение определителя по строке и столбцуСодержание книги
Поиск на нашем сайте
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки d = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i = или j- го столбца d = a1 j A1 j + a2 j A2 j +... + an j An j (j = В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Совместные СЛУ. Теорема Кронеккера-Капелли Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение(совместная система лин. уравнений является определенной тогда и только тогда, когда ранг основной матрицы системы уравнений равен рангу расширенной), и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Теорема Крамера Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*. Очевидно, что система (1) может быть записана в виде: x1 + x2 + … + xn Доказательство. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
x1 = D1/D = 1; x2 = D2/D = 2; Определение общего решения СЛУ. Базисные и свободные неизвестные. Общеерешение системы — совокупность всех частных решений системы. Частноерешение системы — одно из решений неопределенной совместной системы. 27) Однородные СЛУ. Свойства однородной СЛУ. Теорема о нулевом и ненулевом решении СЛУ, Однородная система — система, у которой все свободные члены равны нулю.
Однородная система —всегда совместна, так как x1=x2=x3=...=xn=0является решением системы. Теоремы о ненулевых решениях однородной системы:
Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение. Доказательство: Если у системы уравнений Следствие 2: Однородная система Доказательство: Допустим, система
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.244.92 (0.009 с.) |

 )
)
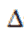 =
=  = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
 не превосходит
не превосходит  . В случае
. В случае 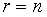 система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при
система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при  .
. , то ранг
, то ранг  , т.е.
, т.е.  . Таким образом, выполняется условие
. Таким образом, выполняется условие  с определителем
с определителем  , имеет ненулевое решение. Тогда по доказанной теореме
, имеет ненулевое решение. Тогда по доказанной теореме 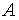 вырожденная, т.е.
вырожденная, т.е.