
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейно зависимые и независимые системы векторов.Содержание книги
Поиск на нашем сайте
Скалярное произведение векторов Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Необходимое и достаточное условие коллинеарности двух векторов. Два вектора Нулевой вектор
Необходимое и достаточное условие компланарности трех векторов. Три вектора Три ненулевых вектора
Операции над векторами, заданными своими координатами. Проекции вектора Длина вектора: Расстояние между точками Действия над векторами в координатной форме. Даны векторы 1. ( 2. l
Скалярное произведение и его свойства. Определение: Под скалярным произведением двух векторов понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. Свойства скалярного произведения: 1. 2. ( 3. 4. 5. 6. два вектора перпендикулярны (ортогональны), если 7. Скалярное произведение в координатной форме имеет вид: Векторное произведение и его свойства. Определение: Под векторным произведением двух векторов -модуль равен площади параллелограмма, построенного на данных векторах, т.е. -этот вектор перпендикулярен перемножаемым векторам, т.е. -если векторы Свойства векторного произведения: 1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 2.Векторный квадрат равен нуль-вектору, т.е. 3.Скалярный множитель можно выносить за знак векторного произведения, т.е. 4.Для любых трех векторов 5.Необходимое и достаточное условие коллинеарности двух векторов Векторное произведение в координатной форме. Если известны координаты векторов Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах
Смешанное произведение и его свойства Определение: Смешанным (векторно-скалярным) произведением векторов Свойства смешанного произведения: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. 2. При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. 3. Необходимое и достаточное условие компланарности трех векторов 4. Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. Если известны координаты векторов
Угол между двумя ненулевыми векторами. Условие перпендикулярности двух векторов. Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Даны два вектора Угол между двумя ненулевыми векторами определяется с помощью вычисления скалярного произведения. ab = |a|*|b|*cos α В случае трехмерного пространства
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.009 с.) |

 Скалярным произведением векторов
Скалярным произведением векторов  (a1;a2)и
(a1;a2)и  (b1;b2) называется число a1b1+a2b2
(b1;b2) называется число a1b1+a2b2 .
.
 коллинеарен любому вектору.Два ненулевых вектора
коллинеарен любому вектору.Два ненулевых вектора  называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней. ,
,  ,
, 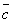 компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
компланарны, Û когда один из них является линейной комбинацией двух других, т.е.

 и
и 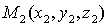 вычисляется по формуле:
вычисляется по формуле:  .
. и
и 
 =
= 
 ,
, 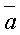 и
и  ×
×  =
= 
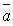 +
+ 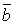 )
) 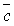 =
= 


 , где
, где  – скаляры.
– скаляры. .
. тогда и только тогда, когда
тогда и только тогда, когда  .
. , где
, где 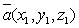 и
и  .
.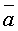 и
и  понимается вектор,
понимается вектор,  для которого:
для которого: , где
, где  угол между векторами
угол между векторами 

 неколлинеарны, то они образуют правую тройку векторов.
неколлинеарны, то они образуют правую тройку векторов.
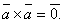

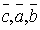 справедливо равенство
справедливо равенство 
 и
и  :
: 
 и
и  , то их векторное произведение находится по формуле:
, то их векторное произведение находится по формуле: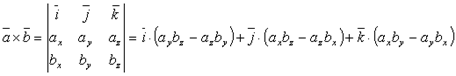 .
.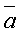 и
и  , вычисляется по формуле:
, вычисляется по формуле:
 .
. .
.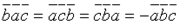 .
. =0.
=0. .
. , то смешанное произведение находится по формуле:
, то смешанное произведение находится по формуле: 
 (xa; ya) и
(xa; ya) и 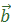 (xb; yb). Эти векторы будут перпендикулярны, если выражение xaxb+ yayb = 0.
(xb; yb). Эти векторы будут перпендикулярны, если выражение xaxb+ yayb = 0.



