
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие вектора. Равные и коллинеарные векторы.Содержание книги
Поиск на нашем сайте
Ответы на коллоквиум Понятие вектора. Равные и коллинеарные векторы. Вектором называется направленный отрезок. Векторы AB и CD называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы AB и CD называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора
Суммой векторов Разностью векторов Суммойтрех векторов называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Умножение вектора на число. Произведением вектора
Линейно зависимые и независимые системы векторов.
Скалярное произведение векторов Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Необходимое и достаточное условие коллинеарности двух векторов. Два вектора Нулевой вектор
Необходимое и достаточное условие компланарности трех векторов. Три вектора Три ненулевых вектора
Операции над векторами, заданными своими координатами. Проекции вектора Длина вектора: Расстояние между точками Действия над векторами в координатной форме. Даны векторы 1. ( 2. l
Скалярное произведение и его свойства. Определение: Под скалярным произведением двух векторов понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е. Свойства скалярного произведения: 1. 2. ( 3. 4. 5. 6. два вектора перпендикулярны (ортогональны), если 7. Скалярное произведение в координатной форме имеет вид: Векторное произведение и его свойства. Определение: Под векторным произведением двух векторов -модуль равен площади параллелограмма, построенного на данных векторах, т.е. -этот вектор перпендикулярен перемножаемым векторам, т.е. -если векторы Свойства векторного произведения: 1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 2.Векторный квадрат равен нуль-вектору, т.е. 3.Скалярный множитель можно выносить за знак векторного произведения, т.е. 4.Для любых трех векторов 5.Необходимое и достаточное условие коллинеарности двух векторов Векторное произведение в координатной форме. Если известны координаты векторов Тогда из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах
Параметрические и каноническое уравнения прямой на плоскости Векторно-параметрическое уравнение прямой: где
В координатах (параметрические уравнения):
Каноническое уравнение прямой
Ответы на коллоквиум Понятие вектора. Равные и коллинеарные векторы. Вектором называется направленный отрезок. Векторы AB и CD называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы AB и CD называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора
Суммой векторов Разностью векторов Суммойтрех векторов называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Умножение вектора на число. Произведением вектора
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.48 (0.006 с.) |

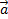 обозначим |
обозначим | 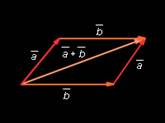 Сложение и вычитание векторов.
Сложение и вычитание векторов. (a1;a2) и
(a1;a2) и  (b1;b2) называется вектор
(b1;b2) называется вектор  (a1+b1;a2+b2)
(a1+b1;a2+b2) (c1;c2) который в сумме с вектором
(c1;c2) который в сумме с вектором  Скалярным произведением векторов
Скалярным произведением векторов  .
.
 коллинеарен любому вектору.Два ненулевых вектора
коллинеарен любому вектору.Два ненулевых вектора  называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней. ,
,  ,
, 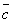 компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
компланарны, Û когда один из них является линейной комбинацией двух других, т.е.

 и
и 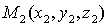 вычисляется по формуле:
вычисляется по формуле:  .
. и
и 
 =
= 
 ,
, 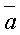 и
и  ×
×  =
= 
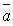 +
+ 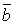 )
) 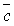 =
= 


 , где
, где  – скаляры.
– скаляры. .
. тогда и только тогда, когда
тогда и только тогда, когда  .
. , где
, где 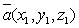 и
и  .
.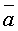 и
и  понимается вектор,
понимается вектор,  для которого:
для которого: , где
, где  угол между векторами
угол между векторами 

 неколлинеарны, то они образуют правую тройку векторов.
неколлинеарны, то они образуют правую тройку векторов.
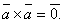

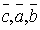 справедливо равенство
справедливо равенство 
 и
и  :
: 
 и
и  , то их векторное произведение находится по формуле:
, то их векторное произведение находится по формуле: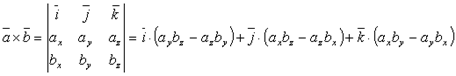 .
.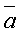 и
и  , вычисляется по формуле:
, вычисляется по формуле:

 - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой; - направляющий вектор.
- направляющий вектор.





