
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о произведении определителей и обратной матрице. Правило Крамера.Содержание книги
Поиск на нашем сайте
ТЕОРЕМА (о произведении определителей). Определитель произведения двух квадратных матриц ДОКАЗАТЕЛЬСТВО. Рассмотрим вспомогательный определитель порядка
Используя теорему Лапласа, вычислим
Вычислим Тогда Пусть ЛЕММА (к теореме об обратной матрице). (а) если (б) если обратная матрица для ДОКАЗАТЕЛЬСТВО. (а) Имеем (б) Пусть Оказывается утверждение (а) можно обратить. ТЕОРЕМА (об обратной матрице). Если матрица
Иными словами, ДОКАЗАТЕЛЬСТВО. Найдем
Но по следствиям 1 и 2 из теоремы Лапласа сумма в скобках равна Пример 7. Дана матрица
Тогда
Линейным уравнением от
Поэтому системой линейных уравнений (СЛУ) называется система вида
Эта СЛУ состоит из
СЛУ (5) называется крамеровской, если число уравнений в ней равно числу неизвестных ПРАВИЛО КРАМЕРА. Крамеровская СЛУ имеет единственное решение
где ДОКАЗАТЕЛЬСТВО. Так как
Вспоминая, чему равна матрица
Но по следствию 1 из теоремы Лапласа числитель (7) есть Пример 8. Решить систему уравнений
Решение.
т. о. ЗАДАЧИ К ГЛАВЕ I. Вычислить выражения: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Вычислить определители: 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49.
Доказать, что система имеет единственное решение, и найти его методом Крамера: 50. 51. 52. 53. 54. 55. 56. 57.
58. Определить, при каких значениях a и b система
1) имеет единственное решение; 2) не имеет решений; 3) имеет бесконечно много решений. Найти обратные матрицы для следующих матриц: 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. Решить матричные уравнения: 71. 72. 73. 74. 75. 76. 77. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. §2.1. Арифметическое линейное пространство Рассмотрим множество
Ниже Множество Непосредственно из определения следуют такие свойства сложения векторов в
Умножение числа на вектор обладает следующими свойствами:
Из этих свойств следует, что в сумме нескольких векторов не обязательно расставлять скобки (свойство 1) и она не зависит от порядка следования слагаемых (свойство 4). В сумме векторов можно приводить подобные члены, т.е.
Справедливы также следующие два утверждения: (1) Действительно,
(2) Действительно,
Вектор вида ЛЕММА 1 (о линейно зависимых системах). Система векторов линейно зависима тогда и только тогда, когда один из них линейно выражается через предыдущие (тем более, через оставшиеся). ДОКАЗАТЕЛЬСТВО. Пусть Тогда
Обратно, пусть Тогда Система векторов ЛЕММА 2 (о порождающих). Если система порождающих линейно зависима, то из неё можно удалить подходящий вектор такой, что оставшаяся система векторов также будет системой порождающих. ДОКАЗАТЕЛЬСТВО. Если система порождающих
Так как для всякого
Подставляя в равенство (2) вместо Линейно независимая система порождающих называется базисом Нетрудно понять, что следующая система векторов будет базисом в
Действительно, она линейно независима, т. к. никакой вектор в ней не может быть выражен через предыдущие. С другой стороны, вектор
Аналогично, для любого
ТЕОРЕМА (о базисах). Любые два базиса линейного пространства состоят из одного итого же числа векторов. ДОКАЗАТЕЛЬСТВО.Пусть даны два базиса линейного пространства
Она линейно зависима по лемме 1, т.к.
Рассмотрим систему порождающих
которая линейно зависима, т.к.
При этом вектор
и продолжаем аналогичную процедуру. Т.к.
причем СЛЕДСТВИЕ 1. В пространстве
СЛЕДСТВИЕ2. Любая линейно независимая система векторов дополняема до базиса. ДОКАЗАТЕЛЬСТВО. Припишем к линейно независимой системе векторов СЛЕДСТВИЕ3. Каждая система порождающих содержит базис. Доказательство аналогично предыдущему. □ СЛЕДСТВИЕ4. В Доказательство следует из следствия 1 и теоремы о базисах. □ Линейно независимая система векторов называется максимальной, если при добавлении к ней еще одного вектора она становится линейно зависимой. Поэтому базис можно определить как максимальную линейно независимую систему векторов.
Ранг матриц.
Наивысший порядок минора матрицы, неравного нулю, называется минорным рангом матрицы. Будем смотреть на столбцы, впрочем, как и на строки, матрицы (а) (б) Их можно объединить в одно: для любых Универсальным способом получения подпространств является следующий: надо взять произвольное множество ТЕОРЕМА (о ранге матриц). Ранг матрицы по столбцам равен ее минорному рангу.
ДОКАЗАТЕЛЬСТВО. Если в матрице любые Обратно, пусть минорный ранг матрицы
Здесь
Заметим, что
Это равенство справедливо при любом
Итак, первые Так как при транспонировании матрицы ее минорный ранг не меняется, то получаем: СЛЕДСТВИЕ 5. Ранг матрицы по строкам равен ее рангу по столбцам. □ СЛЕДСТВИЕ 6. Квадратная матрица является невырожденной тогда и только тогда, когда ее строки (столбцы) образуют линейно независимую систему строк (столбцов). □ Доказательство теоремы о ранге дает и метод вычисления ранга матрицы. Именно, найдя минор Она дает также и способ нахождения максимальной линейно независимой системы строк (столбцов) матрицы. Именно, это будут те строки (столбцы), в которых лежит минор наивысшего порядка, не равный нулю. Пример 1. Найти ранг матрицы
Решение. Минор второго порядка, стоящий в левом верхнем углу этой матрицы отличен от нуля.
Минор третьего порядка
окаймляющий
т. е. ранг матрицы
Назовём элементарными следующие преобразования матриц: - перестановка строк (столбцов); - домножение строки (столбца) на число, отличное от нуля; - добавление к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число; - вычёркивание нулевой строки (столбца). УТВЕРЖДЕНИЕ 1. Элементарные преобразования не меняют ранга матрицы. □ УТВЕРЖДЕНИЕ 2. Система из
линейно независима. □ В заключении укажем ещё один алгоритм нахождения ранга матриц, основанный на утв. 1, 2: с помощью элементарных преобразований приведём матрицу к ступенчатому виду; количество её строк и будет рангом матрицы.
Пример 2. Найти ранг матрицы
Решение. Домножим первую строку матрицы на (-2), (-3), (-1) и прибавим, соответственно, ко второй, третьей и четвёртой строкам, получим
Теперь домножим вторую строку матрицы на (-1) и прибавим к третьей и четвёртой строкам. Вычеркнув нулевую строку, получим матрицу
ступенчатого вида, у которой три строки. Т. е. ранг матрицы равен трём.
Системы линейных уравнений. Общий вид СЛУ задается системой:
Набор чисел Классической является следующая ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ. Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной. ДОКАЗАТЕЛЬСТВО. Пусть СЛУ (*) имеет частное решение Обратно, пусть ранг основной матрицы СЛУ равен рангу расширенной. С точностью до перестановки уравнений и переименования неизвестных можно считать, что минор наивысшего порядка r находится на пересечении первых r строк и столбцов основной матрицы. Следовательно, существуют такие числа Две СЛУ от одного и того же числа неизвестных называются равносильными, если они обе не совместны, либо множества их частных решений равны. Нетрудно показать, что полученная СЛУ равносильна исходной, если - из СЛУ вычеркнуть уравнение вида - обе части какого-то уравнения СЛУ умножить на число, отличное от нуля; - прибавить к одному из уравнений другое, умноженное на некоторое число. Изложим один метод решения СЛУ (*), называемый методом последовательного исключения переменных (или методом Гаусса). Будем считать, что
Полагаем, что
Эта часть метода Гаусса часто носит название «прямого хода». Заметим, что число
Она равносильна исходной и называется общим решением СЛУ (*). Теперь подставляя вместо неизвестных произвольные значения
Пример 3. Реш
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1031; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.171.188 (0.014 с.) |

 и
и  одного и того же порядка равен произведению их определителей, т.е.
одного и того же порядка равен произведению их определителей, т.е. 


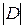 , разлагая его по первым
, разлагая его по первым  строкам. Так как в них лишь один минор
строкам. Так как в них лишь один минор  может быть не равен
может быть не равен  , а его алгебраическое дополнение есть
, а его алгебраическое дополнение есть  , то
, то  . Используя свойство 9 определителей, добьемся, что все элементы
. Используя свойство 9 определителей, добьемся, что все элементы 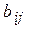 обратились в
обратились в  столбец
столбец  и прибавим к
и прибавим к 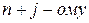 столбцу
столбцу  и
и 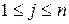 . Получим
. Получим
 , разлагая его по последним
, разлагая его по последним  , где
, где 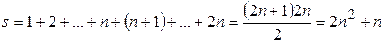 .
.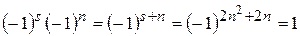 и
и  . Но нетрудно проверить, что
. Но нетрудно проверить, что  . □
. □ матрицы порядка
матрицы порядка  . Матрица
. Матрица  .
. имеет обратную матрицу
имеет обратную матрицу  , то
, то 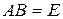 . По теореме о произведении определителей получаем
. По теореме о произведении определителей получаем 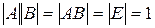 . Значит
. Значит 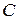 также обратная матрица для
также обратная матрица для  . □
. □ , где
, где (4)
(4) элемент
элемент  элемента
элемента  .
. , и равна 0, если
, и равна 0, если  . Следовательно
. Следовательно  . Аналогично, используя замечание после следствия 2, доказывается, что
. Аналогично, используя замечание после следствия 2, доказывается, что  . □
. □ . Её определитель
. Её определитель  , поэтому обратная матрица
, поэтому обратная матрица 
 ;
;
 ;
;
 ;
;
 ;
; .
.
 называется уравнением вида
называется уравнением вида .
. (5)
(5) уравнений от
уравнений от  , составленная из коэффициентов при неизвестных, называется основной, а если к ней приписать столбец из
, составленная из коэффициентов при неизвестных, называется основной, а если к ней приписать столбец из 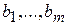 - свободных членов СЛУ (5), то полученную матрицу называют расширенной. СЛУ (5) можно записать и в матричном виде
- свободных членов СЛУ (5), то полученную матрицу называют расширенной. СЛУ (5) можно записать и в матричном виде (6)
(6) и основная матрица ее невырожденная.
и основная матрица ее невырожденная.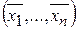 , которое находится по формулам
, которое находится по формулам ,
, определитель основной матрицы СЛУ, а
определитель основной матрицы СЛУ, а  получается из
получается из  в результате замены в
в результате замены в  столбца на столбец из свободных членов.
столбца на столбец из свободных членов. (7)
(7)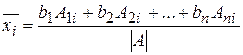 (8)
(8) столбцу. □
столбцу. □
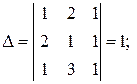


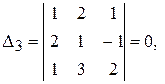










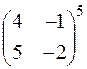
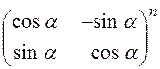


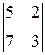



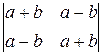









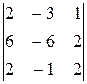
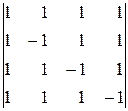







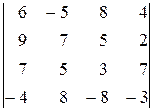
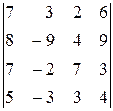







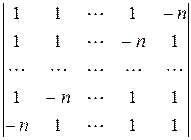














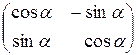

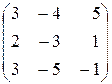


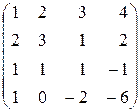
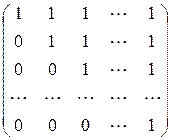









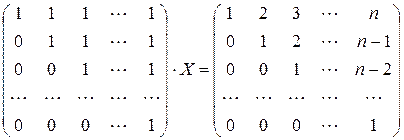
 .
. (строк из
(строк из  . Введем на этом множестве умножение числа на
. Введем на этом множестве умножение числа на  и сложение
и сложение 
 будем называть векторами, и обозначать латинскими буквами
будем называть векторами, и обозначать латинскими буквами  возможно с нижними индексами. Исключение составит нулевой вектор
возможно с нижними индексами. Исключение составит нулевой вектор  . Числа из
. Числа из  будем обозначать греческими буквами
будем обозначать греческими буквами 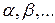


 , а также в равенстве двух сумм переносить вектор из одной части в другую с противоположным знаком.
, а также в равенстве двух сумм переносить вектор из одной части в другую с противоположным знаком.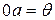 .
.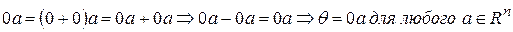 .
. .
. .
. называется линейной комбинацией векторов
называется линейной комбинацией векторов 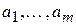 (с коэффициентами
(с коэффициентами  ). Говорят, что система векторов
). Говорят, что система векторов 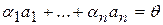 влечет, что
влечет, что  . В противном случае система векторов
. В противном случае система векторов  . Равенство
. Равенство  - наибольший из индексов таких, что
- наибольший из индексов таких, что  .
. , откуда
, откуда
 .
.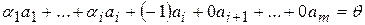 и видно, что в этой линейной комбинации векторов
и видно, что в этой линейной комбинации векторов  не равен нулю. □
не равен нулю. □ называется системой порождающих (или образующих) линейного пространства
называется системой порождающих (или образующих) линейного пространства  , если любой вектор из
, если любой вектор из 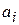 , который выражается через
, который выражается через  :
: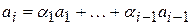 (1)
(1) найдутся числа
найдутся числа  такие, что
такие, что . (2)
. (2) :
:
 имеет вид
имеет вид  и тогда
и тогда .
.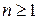 в
в 
 и
и  , причем
, причем  . Рассмотрим систему
. Рассмотрим систему .
. выражается через
выражается через  , но разумеется также является системой порождающих. По лемме 2 из нее можно вычеркнуть некоторый вектор, выражающийся через предыдущие, получив систему порождающих
, но разумеется также является системой порождающих. По лемме 2 из нее можно вычеркнуть некоторый вектор, выражающийся через предыдущие, получив систему порождающих (3)
(3)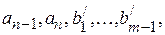 (4)
(4) выражается через систему (3). По лемме 2 из нее можно вычеркнуть некоторый вектор, линейно выражающийся через предыдущие, получив систему порождающих
выражается через систему (3). По лемме 2 из нее можно вычеркнуть некоторый вектор, линейно выражающийся через предыдущие, получив систему порождающих
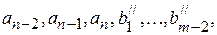
 (5)
(5) . Следовательно, вектор
. Следовательно, вектор  линейно выражается через систему векторов (5), что противоречит линейной независимости
линейно выражается через систему векторов (5), что противоречит линейной независимости  □
□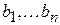 , составляющие базис, получив систему
, составляющие базис, получив систему  . Теперь начнем из этой системы вычёркивать, пока это возможно, векторы, линейно выражающиеся через предыдущие. По лемме 1 векторы вида
. Теперь начнем из этой системы вычёркивать, пока это возможно, векторы, линейно выражающиеся через предыдущие. По лемме 1 векторы вида 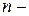 мерном линейном пространстве любые
мерном линейном пространстве любые  векторов образуют линейно зависимую систему.
векторов образуют линейно зависимую систему. как на векторы пространства
как на векторы пространства  (соответственно,
(соответственно,  линейного пространства является его подпространством, если для всех
линейного пространства является его подпространством, если для всех 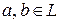 и числа
и числа  выполнены два условия:
выполнены два условия: ;
; .
.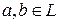 и чисел
и чисел  вектор
вектор  . В этом случае нетрудно проверить выполнение всех свойств 1-8 сложения и умножения числа на вектор из § 2.1. Поэтому подпространства в свою очередь являются пространствами, т.к. условия 1-8 фактически являются аксиомами «быть пространством» для множества элементов
. В этом случае нетрудно проверить выполнение всех свойств 1-8 сложения и умножения числа на вектор из § 2.1. Поэтому подпространства в свою очередь являются пространствами, т.к. условия 1-8 фактически являются аксиомами «быть пространством» для множества элементов  столбцов линейно зависимы, то, по свойству 8 определителя, любой минор
столбцов линейно зависимы, то, по свойству 8 определителя, любой минор  порядка равен нулю. Поэтому минорный ранг не больше ранга по столбцам.
порядка равен нулю. Поэтому минорный ранг не больше ранга по столбцам. равен
равен  . Так как при расстановке строк и столбцов матрицы ее ранг не меняется, то можно считать, что минор
. Так как при расстановке строк и столбцов матрицы ее ранг не меняется, то можно считать, что минор 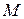
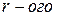 порядка, не равный
порядка, не равный 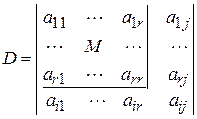
 . Если
. Если  , то
, то  содержит две равные строки и, по свойству 4 определителей, равен
содержит две равные строки и, по свойству 4 определителей, равен  , то
, то  минор
минор 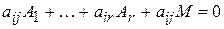 (6)
(6) ,
,  . Из равенства (6) получаем:
. Из равенства (6) получаем: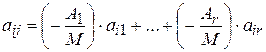
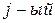 столбец исходной матрицы равен линейной комбинации ее первых
столбец исходной матрицы равен линейной комбинации ее первых 
 порядка, не равный
порядка, не равный 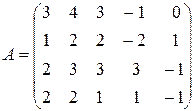 .
.

 , отличен от нуля, однако оба минора четвёртого порядка, окаймляющие
, отличен от нуля, однако оба минора четвёртого порядка, окаймляющие  , равны нулю:
, равны нулю:
 векторов
векторов
 .
.

 такой, который при подстановке вместо
такой, который при подстановке вместо  , каждое из уравнений системы обращает в тождество, называется ее частным решением. Найти общее решение СЛУ, значит указать метод, позволяющий получить все частные ее решения. СЛУ называется совместной, если она имеет хотя бы одно частное решение, и несовместной – иначе.
, каждое из уравнений системы обращает в тождество, называется ее частным решением. Найти общее решение СЛУ, значит указать метод, позволяющий получить все частные ее решения. СЛУ называется совместной, если она имеет хотя бы одно частное решение, и несовместной – иначе.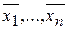 . Видно, что столбец из свободных членов СЛУ является линейной комбинацией столбцов ее основной матрицы. Поэтому ранг основной матрицы равен рангу расширенной.
. Видно, что столбец из свободных членов СЛУ является линейной комбинацией столбцов ее основной матрицы. Поэтому ранг основной матрицы равен рангу расширенной. , что столбец из свободных членов равен линейной комбинации первых
, что столбец из свободных членов равен линейной комбинации первых 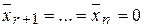 , видно, что
, видно, что  (
( ) является решением
) является решением  ;
; (этого можно всегда добиться с помощью перестановок строк). Попытаемся теперь, умножая первое уравнение на подходящие числа и прибавляя его к последующим, уничтожить в них слагаемые, содержащие
(этого можно всегда добиться с помощью перестановок строк). Попытаемся теперь, умножая первое уравнение на подходящие числа и прибавляя его к последующим, уничтожить в них слагаемые, содержащие  . Для этого, умножаем первое уравнение на
. Для этого, умножаем первое уравнение на  и прибавляем ко второму, и так далее, пока не умножим первое уравнение на
и прибавляем ко второму, и так далее, пока не умножим первое уравнение на 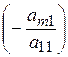 и не прибавим к последнему. Получим равносильную СЛУ вида
и не прибавим к последнему. Получим равносильную СЛУ вида
 (этого можно добиться, переставляя строки или переименовывая переменные). Затем временно «забываем» про первое уравнение и продолжаем такую процедуру с оставшимися. Если в результате этой процедуры возникнет уравнение вида
(этого можно добиться, переставляя строки или переименовывая переменные). Затем временно «забываем» про первое уравнение и продолжаем такую процедуру с оставшимися. Если в результате этой процедуры возникнет уравнение вида  и
и 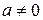 , то система несовместна, если же одно из уравнений окажется вида
, то система несовместна, если же одно из уравнений окажется вида 
 через
через  . Зная это выражение из предпоследнего уравнения можно выразить
. Зная это выражение из предпоследнего уравнения можно выразить  также через
также через 
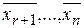 и вычисляя
и вычисляя  можно получить все частные решения (
можно получить все частные решения (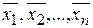 ) СЛУ (*).
) СЛУ (*).


