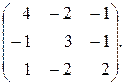Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристические корни и собственные значения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть
Определитель матрицы ( Многочлен ТЕОРЕМА (о характеристических многочленах). Подобные матрицы обладают одинаковыми характеристическими многочленами и, следовательно, одинаковыми характеристическими корнями. ДОКАЗАТЕЛЬСТВО. Пусть, в самом деле,
что и требовалось доказать. □ Из этого результата вытекает, ввиду доказанной в §3.1 теоремы о связи матриц линейного оператора в разных базисах: СЛЕДСТВИЕ. Линейный оператор Эти корни можно называть поэтому характеристическими корнями самого оператора Укажем одно из применений характеристических корней. Пусть в линейном пространстве
где Заметим, что так как ТЕОРЕМА (о собственных значениях). Действительные характеристические корни линейного оператора ДОКАЗАТЕЛЬСТВО. Пусть, в самом деле, оператор
является собственным вектором оператора
Как доказано в §3.1,
Равенства (7) и (8) приводят к системе равенств
Так как
обладает ненулевым решением, а поэтому ее определитель равен нулю,
или Обратно, пусть
то имеют место равенства (9). Обозначим через В заключении отметим, что совокупность собственных векторов линейного оператора Пример 3. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей
Решение: Составим характеристическое уравнение
Раскрывая определитель, получим уравнение
корни которого Найдём собственные векторы, соответствующие собственному значению
После преобразования получим:
Фундаментальная система решений имеет вид:
Собственный вектор Аналогично, для
фундаментальным решением которой будет:
и
ЗАДАЧИ К ГЛАВЕ III. Векторы 110. 111. 112. 113. 114. 115.
Доказать, что системы векторов 116.
117.
Линейный оператор 118.
119.
120. а) б) Найти собственные значения и собственные векторы линейных операторов, заданных в некотором базисе матрицами: 121. 122. 123. 124. 125. 126. 127. 128. 129. 130. 131. 132. ГЛАВА 4.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 квадратная матрица порядка
квадратная матрица порядка  с действительными элементами. Пусть, с другой стороны,
с действительными элементами. Пусть, с другой стороны,  некоторое неизвестное. Тогда матрица (
некоторое неизвестное. Тогда матрица ( ), где
), где  единичная матрица порядка
единичная матрица порядка  . Так как в матрице (
. Так как в матрице ( ) по главной диагонали стоит
) по главной диагонали стоит  , все же остальные элементы равны нулю, то
, все же остальные элементы равны нулю, то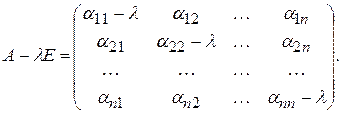
 , все же остальные члены определителя не содержат по меньшей мере двух из числа элементов, стоящих на главной диагонали, и поэтому их степень относительно
, все же остальные члены определителя не содержат по меньшей мере двух из числа элементов, стоящих на главной диагонали, и поэтому их степень относительно  . Коэффициенты этого многочлена можно было бы легко найти. Так, коэффициент при
. Коэффициенты этого многочлена можно было бы легко найти. Так, коэффициент при 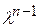 равен
равен  , а свободный член совпадает с определителем матрицы
, а свободный член совпадает с определителем матрицы 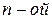 степени
степени 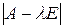 называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы 
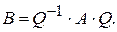 Тогда, учитывая, что матрица (
Тогда, учитывая, что матрица ( , а
, а  получаем:
получаем:
 может задаваться в разных базисах различными матрицами, однако все эта матрицы имеют один и тот же набор характеристических корней. □
может задаваться в разных базисах различными матрицами, однако все эта матрицы имеют один и тот же набор характеристических корней. □ задан линейный оператор
задан линейный оператор  , отличный от нуля, переводится оператором
, отличный от нуля, переводится оператором  (6)
(6) некоторое действительное число, то вектор
некоторое действительное число, то вектор  .
.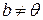 , то число
, то число  матрицу
матрицу 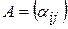 и пусть вектор
и пусть вектор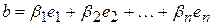
 (7)
(7) (8)
(8) (9)
(9) равны нулю. Таким образом, ввиду (9), система линейных однородных уравнений
равны нулю. Таким образом, ввиду (9), система линейных однородных уравнений (10)
(10) (11)
(11) т. е, собственное значение
т. е, собственное значение  (12)
(12) строку координат (12); ясно, что
строку координат (12); ясно, что  . Тогда справедливо равенство (8), а из (9) и (8) следует (7). Вектор
. Тогда справедливо равенство (8), а из (9) и (8) следует (7). Вектор 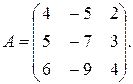
 .
. ,
,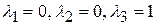 являются собственными значениями линейного оператора
являются собственными значениями линейного оператора  Для этого решим систему (10), считая
Для этого решим систему (10), считая 

 или
или 


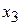

 , получим систему линейных однородных уравнений
, получим систему линейных однородных уравнений
 собственный вектор, соответствующий собственному значению
собственный вектор, соответствующий собственному значению 
 и
и  заданы своими координатами в базисе
заданы своими координатами в базисе 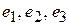 . Показать, что векторы
. Показать, что векторы 










 имеет матрицу
имеет матрицу  :
:



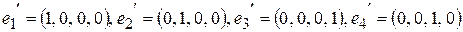 ;
; .
.