
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи на собственные значенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия Большое число научно-технических задач, а также некоторые исследования в области вычислительной математики требует нахождения собственных значений и собственных векторов матриц. Введем некоторые определения для изложения материала данного параграфа. Рассмотрим квадратную матрицу n-го порядка.
Рассмотрим систему Ax=hx (1) Когда система (1) имеет не нулевое решение
или
Выражение (2) называется характеристическим или весовым полиномом относительно h
Корни этого многочлена Они характеризуются тем свойством, что дают нетривиальные решение системы(1) Рассмотрим некоторые из них. Пример Вычислить собственные числа и собственные векторы матрицы
Решение. Составим характеристический многочлен
Для нахождения собственных векторов
Или запишем в виде системы уравнений
Эти уравнения линей зависимы (даже совпадают) поэтому оставим одно из них. Полагаем Аналогично находим первый собственный вектор, соответствующий собственному числу
Отсюда
Вектор Можно даже привести векторы к единичной длине разделив его компоненты на значения модулей векторов. В этом случае
Нахождение наибольшего по модулю собственного значения матрицы А. Пусть имеется характеристический определитель
Корни этого полинома
Укажем приближенный метод нахождения
Проведя преобразование А над вектором
Отсюда, т.к. вектор
AУ- называется итерацией вектора
Выберем в пространстве Пусть Координаты вектора Разлагая собственные векторы Отсюда подставляя (3) в (2) получим (3)
Или меняя порядок суммирования получим
Но Приравнивая (4) и (4а) получим
Разделив (6) на (5) получим
Пусть
1. Волков Е.А. Численные методы. 2. Турчак Л.И. Основы числительных методов. 3. Демидович Б.И. и Марон И.А. Основы вычислительной математики. 4. Копченова И.В. и Марон И.А. Вычислительная математика в примерах и задачах. 5. Перумов У.Г. Числительные методы Высшее образование Москва 2004г.
Содержание Лекция 1. 3 Введение. Численные методы и приближённые вычисления. 3 Методы решения. 4 Абсолютная и относительная погрешность. 4 Погрешность арифметической операции. 4 Лекция 2. 5 Общие понятия об интерполировании. 5 Линейная интерполяция. 6 Интерполяционный многочлен Лагранжа. 7 Оценка погрешности интерполяционной формулы Лагранжа. 8 Исследование остаточного члена при равноотстоящих узлах. 9 Лекция 3. 10 Методы приближенного интегрирования. 10 Формулы Ньютона –Котеса. 10 Частные случаи. 11 Лекция 4. 12 Численное дифференцирование. 12 Метод неопределенных коэффициентов. 14 Лекция 5. 14 Разделённые разности. 14 Интерполяционный полином Ньютона для неравно отстоящих значений аргумента 16 Конечные разности. 17 Связь конечных разностей и разделенных разностей. 18 Интерполяционный полином Ньютона для равноотстоящих значений аргумента. 18 Лекция 6. 19 Классификация уравнений. Этапы численного решения. 19 Отделение корней. 19 Метод половинного деления (бисекций). 22 Метод итераций. 24 Лекция 7. 27 Метод ньютона (касательных). 27
Численные решения СЛАУ. 29 Метод Гаусса. 29 Метод Холецкого. 31 Лекция 8. 32 Метод прогонки. 32 Проверка метода прогонки на устойчивость. 34 Лекция 9. 34 Метод конечных разностей решение краевых задач ОДУ. 34 Лекция 10. 36 Сплайны. 36 Кубический сплайн. 36 Лекция 11. 37 Абсолютная величина и норма матрицы. 37 Метод простой итерации. 39 Оценка погрешности метода простой итерации. 39 Лекция 12. 40 Приведение систем к виду, допускающему применение метода простых итераций. 40 Метод Зейделя. 42 Лекция 13. 43 Методом Зейделя решить систему. 43 Обусловленность систем линейных уравнений число обусловленности. 44 Лекция 14. 46 Численные методы решения задачи Коши для ОДУ. 46 Метод последовательного дифференцирования. 47 Метод Эйлера. 47 Лекция 15. 48 Метод Рунге - Кутта. 48 Лекция 16. 50 Эмпирические формулы.. 50 Метод наименьших квадратов. 50 Лекция 17. 52 Пример: метод наименьших квадратов для вывода эмпирической формулы, заданной в табличном виде: 52 Предварительное вычисления. 54 Лекция 18. 54 Задачи на собственные значения. 54 Основные понятия. 54 Пример. 55 Нахождение наибольшего по модулю собственного значения матрицы А. 56 Содержание. 59
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.201.123 (0.011 с.) |

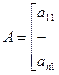
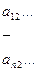
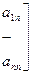
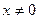
 (1)
(1)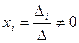 тогда
тогда 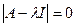 (2)
(2)
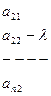
 =0 (2)
=0 (2)
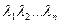 являются собственными значениями матрицы А.
являются собственными значениями матрицы А.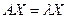 . Чтобы было нетривиальное решение
. Чтобы было нетривиальное решение 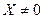 необходимо и достаточно
необходимо и достаточно  стоит один из корней собственного полинома
стоит один из корней собственного полинома 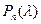 , то выражение (2) обращается в 0. И для этого
, то выражение (2) обращается в 0. И для этого 

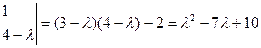
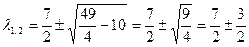
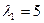
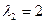
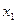 и
и  соответствующих значениям
соответствующих значениям 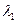 и
и 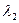 Составим системы уравнений типа
Составим системы уравнений типа 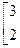

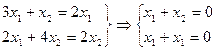

 и собственный вектор соответствующий числу
и собственный вектор соответствующий числу 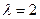 имеет вид
имеет вид  или,
или,  , где
, где  и
и  единичные орты выбранной системы координат.
единичные орты выбранной системы координат.
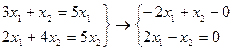
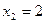
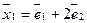
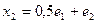

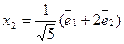
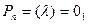
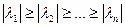 (1)
(1)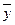 и разложим по собственным векторам
и разложим по собственным векторам 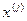 матрицы А.
матрицы А.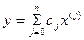 ,где
,где 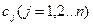 - постоянные коэффициенты
- постоянные коэффициенты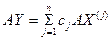
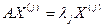 получим
получим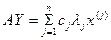
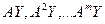 , получим
, получим 
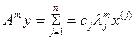 (2) (м-итераций)
(2) (м-итераций)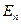 базис
базис  (не обязательно единичный).
(не обязательно единичный).
 в выбранном базисе.
в выбранном базисе. получим
получим 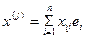
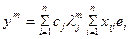
 (4)
(4)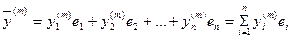 (4а)
(4а)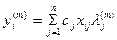 (5)
(5) (6)
(6)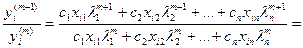
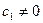 и
и 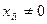 , тогда
, тогда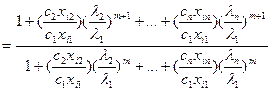
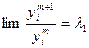 с учётом неравенства (1)
с учётом неравенства (1)


