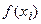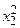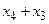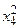Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка погрешности интерполяционной формулы ЛагранжаСодержание книги
Поиск на нашем сайте
R(x) = f(x)-Ln(x) Будем считать, что f(xi) – вычислены точно. Тогда Рассмотрим вспомогательную функцию
или
где
Последняя формула позволяет заранее оценить отклонения функции Ln(x) и выбрать нужное количество узлов n.
Исследование остаточного члена при равноотстоящих узлах.
При интерполировании функций желательно, чтобы модуль Rn(x) принимал наименьшее значение. Поэтому нужно исследовать следующие вопросы. 1) При заданных узлах интерполяции, изучить для каких участков [a,b] остаточный член Rn(x) будет принимать max и min значения. Поведение первого сомножителя Естественно ожидать, что вблизи больших по модулю экстремумов Поведение 1) 2) Т.к.
Тогда экстремальные значения
Следовательно, ошибка интерполяции меньше на середине отрезка и больше к концам отрезка. Вне отрезка [a,b]
Лекция 3
Методы приближенного интегрирования. Формулы Ньютона –Котеса. Один из методов приближенного интегрирования
В этом случае, если взять узлы интерполяции равноотстоящими, то xk=x0+k*h k=0,1,2…n x=x0+t*h dx=hdt
x-x1=(x0+th)-(x0+1h)=(t-1)h _ _ _ _ _ _ a=x0=x0+th x-xn=(x0+th)-(x0+nh)=(t-n)h
xk-x0=(x0+kh)-(x0+0h)=kh _ _ _ _ _ b=xn=x0+nh=x0+nh
_ _ _ _ _ _
Частные случаи. n=1 L1(x)=ax+ b
A1(0)=- A1(1)=
n=2 L2(x)=a2 x+ b+c
A2(0)=- A2(1)= A2(2)=
Лекция 4
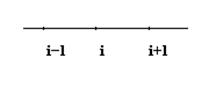
Численное дифференцирование. Напомним, что производной функции y=f(x) называется предел отношения приращения функции ∆y к приращению аргумента Δx при стремление Δx к нулю y`= f `(x)= В численных расчетах на ЭВМ, когда функция задана таблицей значений, значение шага Δx полагают равному конечному числу и для вычисления значений производных получают приближенное равенство y`≈ Это соотношение называется аппроксимацией производных с помощью отношения конечных разностей (т.к. ∆y и Δx конечные в отличие от значений в формуле (1)). Рассмотрим аппроксимацию производной для функции y=f(x), заданной в табличной форме xi= x0, x1… xn yi= y0, y1… yn Пусть шаг разности между соседними значениями аргумента постоянен и равен h. Запишем выражение в точке x=x1
Можно найти производные с помощью формул Тейлора f(x +Δx)= f(x)+
(1) y(xi-1 )=y(xi –h) = y(x)- hf `(xi)+0(h2) yi-1= yi- hf `(xi)+0(h2) y`(xi)=f `(xi)= (2) y(xi+1 )=y(xi +h) = y(x)+ hf `(xi)+0(h2) yi+1=yi+ hf `(xi)+ y`(xi)=f `(xi)= (1) y(xi-1 )=yi –h yi `+ (2) y(xi+1 )=yi +h yi `+ (1)+ (2) yi-1+ yi+1=2 +
(2)- (1) yi+1 -yi-1 =2hyi ` yi `= Можно использовать полиномы Лагранжа и Ньютона. Метод неопределенных коэффициентов.
a=-b=-
И так далее.
Лекция 5
Разделённые разности
Пусть функция f(x) вычислена в точках
Разность вида: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Разность вида:
т. е. узлы можно менять любым образом.
2) Разделённые разности порядка k от
3) Линейность разделённой разности относительно функции, к которой применяется разделённая разность.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1087; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.141.52 (0.009 с.) |

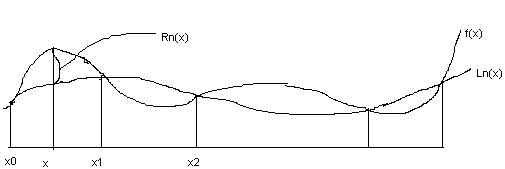
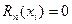 . Если f(x) полином степени меньше или равной n, то при любых x
. Если f(x) полином степени меньше или равной n, то при любых x 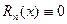 . Пусть f(x) (n+1) раз дифференцируемая на отрезке [a,b] функция.
. Пусть f(x) (n+1) раз дифференцируемая на отрезке [a,b] функция.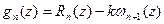 . Очевидно, что
. Очевидно, что 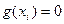 i = 0,1,2,…,n в (n+1) точках. Подберём k таким образом, чтобы в точке
i = 0,1,2,…,n в (n+1) точках. Подберём k таким образом, чтобы в точке 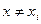 в которой мы хотим оценить полином
в которой мы хотим оценить полином 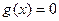 , т.е.
, т.е. 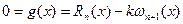 и тогда
и тогда 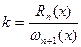 (1). При данном выборе k функция g(z) обращается на [a,b] в нуль в (n+2) точках
(1). При данном выборе k функция g(z) обращается на [a,b] в нуль в (n+2) точках 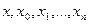 . По теореме Роля производная g’(z) обращается в нуль на [a,b] в (n+1) точке и т.д. Производная (n+1) порядка от g(z) обращается в нуль по крайней мере 1 точке [a,b]. Обозначим через
. По теореме Роля производная g’(z) обращается в нуль на [a,b] в (n+1) точке и т.д. Производная (n+1) порядка от g(z) обращается в нуль по крайней мере 1 точке [a,b]. Обозначим через 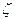 эту точку, тогда
эту точку, тогда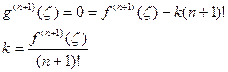 (2)
(2)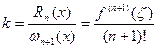 и тогда
и тогда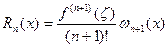 (3)
(3)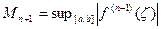 , тогда
, тогда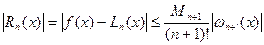 (4)
(4)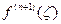 в остаточном члене
в остаточном члене 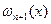 при заданных узлах
при заданных узлах 
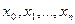 . Полином
. Полином  и меняет знак при переходе через каждый узел. Между узлами имеет место min и max.
и меняет знак при переходе через каждый узел. Между узлами имеет место min и max.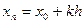 , положив
, положив 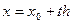 и тогда
и тогда 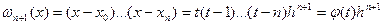
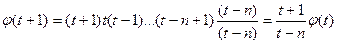
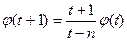
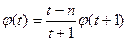
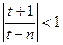 при
при 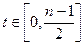 , то
, то 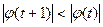
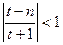 при
при 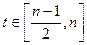 , то
, то 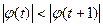
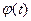 на отрезке [k,k+1] будут max по абсолютной величине на крайних точках [0,1], [n-1,n] и min в середине, следовательно
на отрезке [k,k+1] будут max по абсолютной величине на крайних точках [0,1], [n-1,n] и min в середине, следовательно 
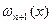 будет возрастать.
будет возрастать. f(x)d(x) заключается в замене функции f(x) на какой- либо интерполяционный полином. Например
f(x)d(x) заключается в замене функции f(x) на какой- либо интерполяционный полином. Например

 x-x0=(x0+th)-(x0+0h)=th
x-x0=(x0+th)-(x0+0h)=th t=0
t=0 xk-xk-1=(x0+kh)-(x0+(k-1)h)=1h
xk-xk-1=(x0+kh)-(x0+(k-1)h)=1h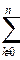
 dt*
dt* 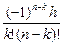 f(xk)=
f(xk)= 
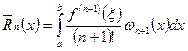
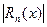
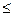

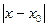
 …
…  dx=
dx= 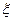
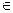 [a, b]
[a, b]
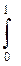
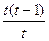 dt=
dt= 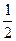
 dt=
dt= 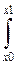 f(x)dx=h(
f(x)dx=h(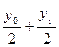 )=
)= 
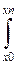 f(x)dx=
f(x)dx= 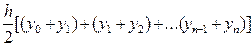 = h[
= h[ 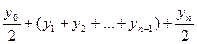 ]
]
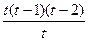 dt=
dt= 
 dt=
dt= 
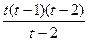 dt=
dt=  f(x)dx=h(
f(x)dx=h(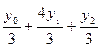 )=
)= 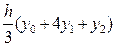
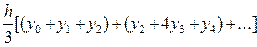 = =
= = 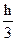 [
[ 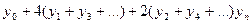 ]
]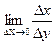 ∆y= f(x +Δx)- f(x) (1)
∆y= f(x +Δx)- f(x) (1)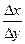 (2)
(2)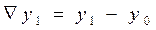 ∆x=h
∆x=h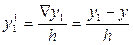 (3)
(3)
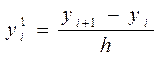 ~0(h)
~0(h)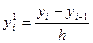 ~0(h)
~0(h)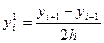 ~0(h2)
~0(h2)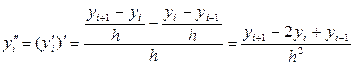 ~0(h2)
~0(h2)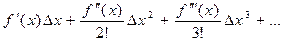
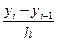 ~0(h)
~0(h) ~0(h)
~0(h)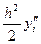 + 0(h3)
+ 0(h3)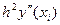
 =
=  ~0(h2)
~0(h2)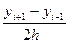 ~0(h2)
~0(h2)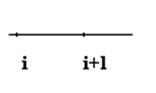
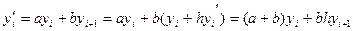
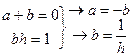

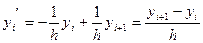

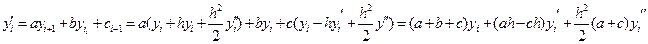
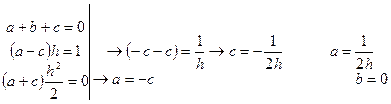
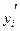 =
= 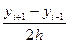
 i=0,1,2,…,n,
i=0,1,2,…,n, 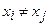 . Тогда выражение
. Тогда выражение называется разделённой разностью 1-го порядка.
называется разделённой разностью 1-го порядка. называется разделённой разностью 2-го порядка
называется разделённой разностью 2-го порядка -называется разделённой разностью к-го порядка. Вычисляются разделённые разности согласно Таблицы №1.
-называется разделённой разностью к-го порядка. Вычисляются разделённые разности согласно Таблицы №1.


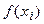
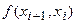



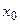
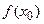
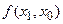
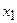



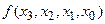



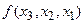

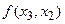



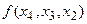
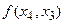



 1) Разделённые разности симметричны относительно своих аргументов
1) Разделённые разности симметричны относительно своих аргументов 
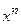 являются однородным многочленом относительно своих аргументов степени n-k, при n=k она равна 1, а при k>n она равна 0.
являются однородным многочленом относительно своих аргументов степени n-k, при n=k она равна 1, а при k>n она равна 0.