Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методом Зейделя решить системуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2,2x1+9,1x2+4,4x3=9,7 Ax=U -1,3x1+0,2x2+5,8x3=1,4 Решение приведем систему к виду, допускающему применение итерационных методов x =Bx+V
1) За нулевые приближение возьмем 2) Строим процесс по методу Зейделя.
Второе приближение
Решение приводим в таблице
Посторенние итерации заканчивается, когда с заданной точностью получаем значения в двух итерациях в конкретном примере. x1≈0,247 x2≈1,114 x3≈-0,224 Проверим, сходиться ли метод Зейделя для данного примера
Сходится, т.к. Обусловленность систем линейных уравнений число обусловленности. Задача над плохо обусловленной, если вычисляемые величины X очень чувствительны к небольшим изменениям исходных данных. Рассмотрим причины, определяющие решения X систем Ax=U (1) Изменим правую часть U на U+δU, это приведет к изменениям решения x на x+δx и при постоянной матрице A, имеем: A(x+ δx) = U+δU (2) Из (1) Из (2) имеем Aδx=δUàδx=A-1δU=> Перемножим (3) и (4) получим
Число k(A)= (A+ δA)(x+ δx)=U Из (1) имеем x=A-1U (6) x+ δx= (A+ δA) -1U (6a) A-1U+ δx= (A+ δA) -1U=> δx= [(A+ δA) -1- A-1]U=> (7) (A+ δA) -1- A-1=[I- A-1 (A+ δA) ] (A+ δA) -1=-A-1δA(A+δA)-1 Подставляя в (7) получим δx=-A-1δA(A+ δA) -1U δx=-A-1δA(x+ δx)
Число обусловленности обладает рядом свойств 1) k(CA)= 2) k(A)=k(A-1) 3) k(A)= 4) Если m-min значение матрицы; M-max значение матрицы, то
Отсюда следует наличие малого собственного значения матрицы А обязательно означает её плохую обусловленность. Однако матрица А может быть плохо обусловленной, когда у неё нет малого собственного значения. Например, наименьшее собственное значение матрицы 100 го порядка Равен m=0,501. Если же рассмотреть систему Ax=U c
То получим
Первая компонента решения Ax=U система больше, чем 1022, т.е. Отсюда
В свою очередь для любой матрицы
Матрица плохо обусловлена Пример Рассмотрим систему
Точное решение x=1 и y=1 В рассматриваемом примере матрица системы AX=U симметрична и имеет собственное значение m=0,00005 M=1,98005 Здесь Система плохо обусловлена, а значит следует ожидать, что малые значения (сдвиг) правых частей приведут к большому изменению решения
x+0, 99y=1, 989903 0, 99x + 0,98y=1,970106 То получим решение x=3,000 y=-1,0203, т.е. Здесь Значит небольшое изменение δU влечет за собой изменение относительной погрешности вычислительных величин Лекция 14
Численные методы решения задачи Коши для ОДУ. Пусть имеем уравнение n-го порядка
Y(xk)=y0(k) k=0,1,2…n-1 Эта задача сводится следующей системе дифференцированных уравнений первого порядка
Тогда
Тогда уравнение (1) запишется
Пример
Тогда (2) Запишется в виде (2) Метод последовательного дифференцирования. Пусть есть Решение можно записать в виде ряда Тейлора
Здесь Y(k)(x0) заданы начальными условиями. Пример
Метод Эйлера
Этот метод получается, если в формуле Тейлора удержать только 2 числа первых.
По этому методу интегральная кривая заменяется на касательную к интегральной кривой. Этим методом находится решение на отрезке [x0,x0+h] затем счет повторяется.
Найденные точки ломаной M0M1…MN позволяет построить ломаную, называемой ломаной Эйлера. Точность метода 0(h), остаточный член 0(h2). Чем меньше возьмем h, тем точнее будет результат.
Лекция 15 Метод Рунге - Кутта Один из наиболее употребительных методов с повышенной точностью является методов Рунге – Кутта. Мы будем рассматривать этот метод для уравнения 1-го порядка.
Если правая часть уравнения
Будем искать решение
ξ0=х0 η0=у0 ξi=x0 +aih ηi=y0+ и будем рассматривать функцию φr(h)= Причем Pri, ai и βij- некоторые const подлежащие определению и определяются так, чтобы φr(e)(0)=0 e=0,1,2…s φr(s+1)(0)≠0 до величины возможно более высокого порядка S. Тем самым будет охвачена часть формулы Тейлора с соответствующей точностью.
r=1
Таким образом, r=2
Система имеет 4 неизвестных и 3 уравнения, т.е. имеет бесчисленное множество решений Если положить
Лекция 16
Эмпирические формулы Пусть изучая неизвестную функциональную зависимость между
Задача состоит в том, чтобы найти приближённую зависимость y=f(x) (1) Значение которой при Будем считать что тип эмпирической формулы выбран и её можно привести в виде:
Задачи нахождения наилучших значений параметров
Метод наименьших квадратов Запишем сумму квадратов отклонений (3) для всех точек
Параметры
Поскольку здесь параметры
Полученные соотношения – системы управления для определения Рассмотрим применение метода наименьших квадратов для частного случая, широко используемых на примере. В качестве эмпирической формулы рассмотрим многочлен
Формула (4) для определения суммы квадратов отклонений S примет вид
Для составления системы уравнений (5) найдем частные производные функции S=S(
или
Решая последнюю систему относительно Систему (9) можно записать в более компактном виде
где Лекция 17 Пример: метод наименьших квадратов для вывода эмпирической формулы, заданной в табличном виде:
Задана эмпирическая зависимость в табличной форме.
Найти зависимость y=f(x) Решение Если изобразить табличные значения на графике (1) то легко убедиться, что в качестве эмпирической формулы для аппроксимации функции y=f(x) можно принять параболу, т.е.
В данном случае m=2 n=4 и система (10) пример вид
Коэффициенты этой системы могут быть вычислены по формулам (11) i=0,1,2,3,4
Система уравнений (12) запишем в виде
Отсюда находим параметры Оценим относительные погрешности полученной аппроксимации в заданных точках, т.е. найдем значение
Пример Пусть на основании эксперимента получим значения функции y=f(x), которые записаны в таблицу
С помощью метода наименьших квадратов функцию y=f(x) аппроксимировать линейной функцией
Решение Составим систему для определения
Предварительное вычисления
и следовательно
Искомый многочлен y=1,09x-0,28
Лекция 18
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.32.115 (0.009 с.) |

 7,6x1+0,5x2+2,4x3=1,9
7,6x1+0,5x2+2,4x3=1,9

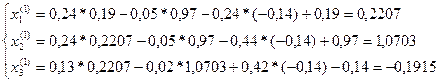 -1-ая приближенность
-1-ая приближенность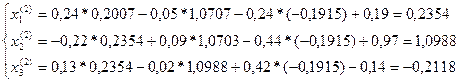

 =0,75<1
=0,75<1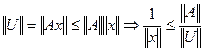 (3)
(3)
 (4)
(4) (5)
(5) называют числом обусловленности. Если число k(A) велико, то для большинства правых частей решение ненадежно. Это же число может быть использовано и для других задач. Пусть, например, δх – погрешность вызвана погрешностью δА элементов матрицы А, а правые части заданны точно, тогда имеем
называют числом обусловленности. Если число k(A) велико, то для большинства правых частей решение ненадежно. Это же число может быть использовано и для других задач. Пусть, например, δх – погрешность вызвана погрешностью δА элементов матрицы А, а правые части заданны точно, тогда имеем
 (8)
(8)
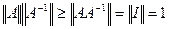 k(A)≥1
k(A)≥1
 и
и 

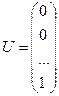 , где
, где 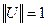 , то имеем
, то имеем
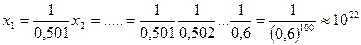
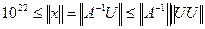

 и следовательно
и следовательно 




 , т.е. рассмотрим систему
, т.е. рассмотрим систему

 на 200%. Задача плохо обусловлена.
на 200%. Задача плохо обусловлена. Y(n)=f(x,y,y`…y(n-1)) (1)
Y(n)=f(x,y,y`…y(n-1)) (1)


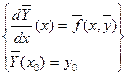 (2)
(2)



 (1)
(1)





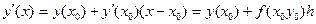

 (1)
(1) непрерывна в окружности точки (х0у0) то решение задачи Коши может быть представлено в виде ряда Тейлора.
непрерывна в окружности точки (х0у0) то решение задачи Коши может быть представлено в виде ряда Тейлора. (2)
(2) (3)
(3)

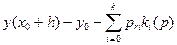

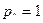
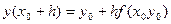 это совпадает с формулой Эйлера. Точность 0(h’), а отличается 0
это совпадает с формулой Эйлера. Точность 0(h’), а отличается 0 
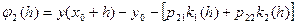

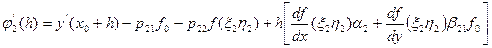

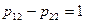


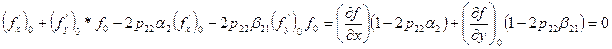

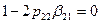
 то
то 

 и тогда какие решения
и тогда какие решения  или до
или до 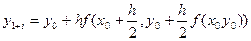
 и
и  мы в результате серии экспериментов получим таблицу значений
мы в результате серии экспериментов получим таблицу значений
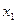




 (i=0,1,2…n) мало отличается от остальных данных. Приближённая функциональная зависимость (1), полученная на основании экспериментальных данных, называется эмпирической функцией.
(i=0,1,2…n) мало отличается от остальных данных. Приближённая функциональная зависимость (1), полученная на основании экспериментальных данных, называется эмпирической функцией.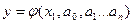 (2) где
(2) где 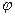 -неизвестная функция
-неизвестная функция 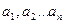 -неизвестные параметры. Задача состоит в том, чтобы определить далее значения этих параметров, при которых эмпирическая формула даёт хорошее приближение данной функцией, значения которой в точки
-неизвестные параметры. Задача состоит в том, чтобы определить далее значения этих параметров, при которых эмпирическая формула даёт хорошее приближение данной функцией, значения которой в точки  равны
равны  (i=0,1,2…n). Разность между этими значениями обозначим через
(i=0,1,2…n). Разность между этими значениями обозначим через 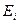
 i=0,1,2…n (3)
i=0,1,2…n (3)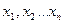 :
: (4)
(4) эмпирической формулы (2) будем находить из условий min функции
эмпирической формулы (2) будем находить из условий min функции  .В этом состоит метод наименьших квадратов.
.В этом состоит метод наименьших квадратов. выступают в роли независимых функций S, то её min найдём приравнивая к нулю частные производные по этим переменным:
выступают в роли независимых функций S, то её min найдём приравнивая к нулю частные производные по этим переменным:
 (5)
(5) (6)
(6) (7)
(7)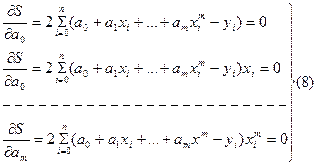

 и получим многочлен (6)
и получим многочлен (6)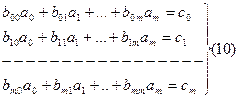

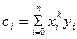
 (m)
(m)
 квадратный трёхчлен
квадратный трёхчлен




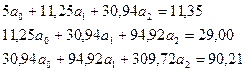


 таким образом
таким образом  (13)
(13) результаты вычисления представим в виде таблицы
результаты вычисления представим в виде таблицы


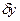

 и
и