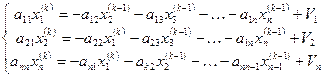Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод конечных разностей решение краевых задач ОДУ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дана краевая задача ОДУ
Требуется решить такое уравнение. Отрезок [a, b] разбивается точками на равные части xj=x0+jh. Точки разделяются на внутренние 1 ≤ j ≤ n-1 и граничные j=0 и j=n. Затем производные входящие в уравнение (1) y`(xi)=
И подставим равенства (*0 в уравнение (1), получим
Преобразуем (2) к виду (3), получишь
c0 y0- b0 y1…………………..=f0 j=0
………………...-an yn-1+cnyn=fn j=n
Или
Полученную систему решаем методом прогонки, которую мы рассматривали в системах линейных уравнений.
Лекция 10
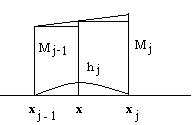
Сплайны. Пусть есть функция f(x) заданная в узлах отрезка [a,b]. Пусть заданны узлы интерполяции x0x1…xn xi Будем приближать функцию f(x) на каждом отрезке ∆~[xj-1xj] полиномом Pj,m(x)=a0j+a1jx+…+ anjxm Сплайном назовем S∆(x) функцию совпадающую на каждом участке [xj-1xj] с полиномом Pj,m(x) и такую, что во всех внутренних узлах непрерывную вместе со своими производными до (m-1) порядка включительно во всех точках xi i=1, n-1. Кубический сплайн. Будем считать, что на каждом участке [xj-1xj] мы приближаем полином 3=ей степени. Pj,3(x)=ax3+bx2+cx+d, тогда
Найдем S∆(x) для чего проинтегрируем дважды (1), получим
Найдем с1 и с2 из условия S∆(xj-1)= y j-1 S∆(xj)= y j
C1hj=yj- Mj C1= C2=
Поскольку S∆`(xj-0)= S∆(xj+0)
Приравнивая получаем
λj= μiMj-1+2Mj+ λj Mj=dj j=1,n-1 Полученная система служит для определения M0 M1… Mn, подставляя в формулы (х) и (х*) получим, что полином удовлетворяет 3-м свойствам 1) S∆(xj-0)= S(xj+0) 2) S`(xj-0)= S` (xj+0) 3) S``(xj-0)= S``(xj+0)
Лекция 11 Абсолютная величина и норма матрицы. Под нормой матрицы A~(aij) понимают действительное число 1) 2) 3) 4) Матрица определяется тремя нормами. 1) 2) 3)
Для матрицы
Найти Решение 1) 2) 3) Для вектора 1) 2) 3)
Пример.
Вычислить Решение
Метод простой итерации. Пусть задана система линейных уравнений Ax=b=>Ax-b=0 (1) Ax`-b=ξ- невязка x- x+ Ax-b=0=>x= (I-A) x+ b=>x=Bx+ b (2) Пусть матрица B невырожденная, т.е. det B≠0/ Выбрав произвольно x0 вычисляем последовательно xk xk= Bxk-1+b (3) Пусть x*- точное решение уравнения (1) и (2), тогда
(xk-x*) =B (xk-1-x*) (4) (xk-x*) =B (xk-1-x*) = B B (xk-2-x*) = Bk (x0-x*) (4a) Пронормируем последнее выражение (4а) получим:
Из полученного неравенства следует, что при произвольном выборе x0 соотношение Эквивалентно Оценка погрешности метода простой итерации. х*= Bx*+b xk= Bxk-1+b Рассмотрим выражение (1) (I-B)(x*-xk)=x*-xk-Bx*+ Bxk= -xk+b+ Bxk=xk+1-xk (I-B)(x*-xk)= xk+1-xk (x*-xk)= (I-B)-1(xk+1-xk) (2) Пронормируем выражение (2) получим
Найдем Рассмотрим для этого тождество (I-B)(I-B)-1=I (I-B) -1- B (I-B)-1=I (I-B) -1=I+ B (I-B)-1
xk+1- xk= B (xk-xk-1) = B B (xk-1-xk-2) = Bk (x1-x0) (4) Подставляя (3) и (4) в формулу (2а) имеем
Эта формула позволяет подсчитать число итераций необходимое для получения приближения с заданной точностью.
Лекция 12 Приведение систем к виду, допускающему применение метода простых итераций. Обычно система линейных уравнений задана в виде
и для приведения её к виду x=Bx+b, допускающего применение метода простых итераций. Подбирают невырожденную матрицу H (det H≠0), так чтобы Ax=b => HAx= Hb=> x- x+ HAx= Hb=> X= x- HAx +V=> x= (I-HA)x+ V Берем B=I-HB Тогда получаем x= Bx+ V, причем
Матрицу H целесообразно близко к A-1 так, чтобы HA~I. Так, например, если в матрице A вдоль главной диагонали элементы преобладают над остальными, то берут
Если матрица A=A* самосопряженная и положительно определенная A*=A и λ у матрицы A положительна, у которой известны её max и min собственные значения.
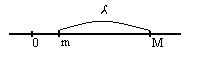
0≤ m≤M, то полная H= tI получим
Т.к. надо найти
1) -(1-tm)=-(1-tM) 2) 1-tm=1-tM 3) -(1-tm)=(1-tM) 4) 1-tm=-(1-tM) (3) и (4) 1-tm=-(1-tM)=>2=t(M+n)=>t= (1) и (2) 1-tm=1-tM=> t(M-m)=0 t=0 это не берем Тогда
х*= Bx*+b xk= Bxk-1+b x*-xk=B(x*-xk-1)=BB(x*-xk-2)=…=Bk(x*-x0)
Получим max скорость сходимости
Пример простой итерации решить систему
Пример Приведем систему к нормальному виду x=Bx+V
x=Bx+ V
=
Тогда x1=2,9935 x2=1,0068 x3=1,0068 Или x1≈3 x2≈1 x3≈1 Метод Зейделя. Решение системы Ax=U по методу Зейделя производится по формулам
Если при вычислении i-той координаты вектора
То вычисления будут проходить по формулам Зейделя.
Лекция 13
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.31.223 (0.01 с.) |



 заменяются в точках хi приближенными конечно-разностными соотношениями.
заменяются в точках хi приближенными конечно-разностными соотношениями. ~0(h) (*)
~0(h) (*) =
=  ~0(h2)
~0(h2)
 =
= 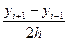 ~0(h2)
~0(h2) (2)
(2)
 (3)
(3) (4) ……-aj yj-1+cj yj-bj yj+1….......=fj 1≤ j≤ n-1
(4) ……-aj yj-1+cj yj-bj yj+1….......=fj 1≤ j≤ n-1

 =
=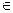 [a,b] в которых заданны значения функции f(x0) f(x1)… f(xn) [x0x1], [x1x2]… [xn-1xn]~∆- разбиения.
[a,b] в которых заданны значения функции f(x0) f(x1)… f(xn) [x0x1], [x1x2]… [xn-1xn]~∆- разбиения.
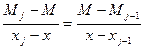
 (1)
(1) 

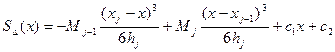
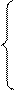

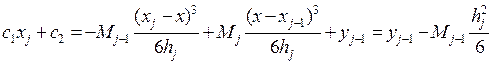
 => C1hj=yj-yj-1+
=> C1hj=yj-yj-1+ 

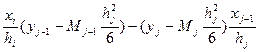
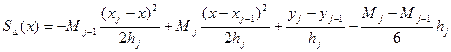

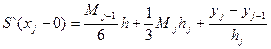
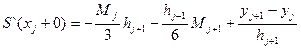
 (2)
(2) μi=
μi=  , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям: (
( где α- число.
где α- число.
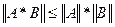
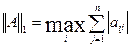







 эти нормы вычисляются по следующим формулам
эти нормы вычисляются по следующим формулам -максимальная из координат вектора взятая по модулю
-максимальная из координат вектора взятая по модулю - сумма модулей координат вектора
- сумма модулей координат вектора -корень квадратный из суммы квадратов модулей координат вектора
-корень квадратный из суммы квадратов модулей координат вектора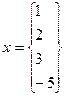





 (5)
(5)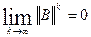 (6) при
(6) при  < 1 (7)
< 1 (7)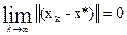 или
или  . Соотношение (6) возможно, если выполнено неравенство (7).
. Соотношение (6) возможно, если выполнено неравенство (7). 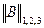 < 1
< 1 (2а)
(2а)


 (3)
(3)
 (5)
(5)
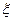





 , то
, то


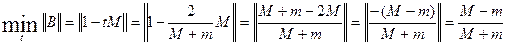



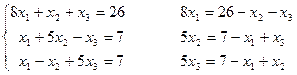



 Метод простой итерации сходится за
Метод простой итерации сходится за






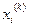 учитывается найденные заранее уже координаты
учитывается найденные заранее уже координаты 
 …
…