
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционный полином Ньютона для неравно отстоящих значений аргументаСодержание книги
Поиск на нашем сайте
Пусть f(x) ¾ некоторая функция, а x0,x1,…xn ¾ узлы интерполяции, а x ¾ произвольная, но фиксированная точка значения аргумента. Тогда имеем:
Откуда:
Аналогично:
Откуда
продолжая этот процесс далее, получим:
Эта форма записи носит название интерполяционной многочлена Ньютона для неравных промежутков или
Можно показать, что полином Ньютона и полином Лагранжа совпадают Nn(x)= Ln(x), т.е. равный их остаточный член.
Или
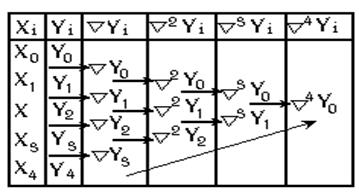
Полином Ньютона удобнее полинома Лагранжа тем, что при добавлении новых узлов интерполяции все проведенные вычисления в полиноме Ньютона сохраняются, а в полиноме Лагранжа нет. Конечные разности. В случаях когда узлы интерполяции берутся равноотстоящими xk=x0+k*h k=0,1,2…n n- шаг интерполирования, то часто вводят следующие обозначения
0нисходящие восходящие - конечная разность 2 го порядка центральные
- конечная разность 3 го порядка
Связь конечных разностей и разделенных разностей. Для равностоящих значений аргумента xk=x0+k*h имеем:
_ _ _ _ _ _ _ _ _ _
Интерполяционный полином Ньютона для равноотстоящих значений аргумента. Если в общей формуле полинома Ньютона Nn(x)= f (x0)+ f (x0 x1)(x-x0)- (x-x0)(x-x1)f (x0x1xn)+ …+….+(x-x0)… (x-xn-1)f (x0x1…xn)+(x-x0)…(x- xn)f (x0x1…xn) (1) В качестве узлов интерполирования можно взять xk=x0+k*h и положить x=x0+t*h k=0,1,2…n, то тогда x- xk=(x0+th)- (x0+kh)= (t-k)h и
Если в уравнении (1) в качестве узлов взять xk=x0+k*h и ввести замену x=x0+t*h, то получим x-xk=(x0+th)-(x0-kh)=(t+k)h
то получим полином для интерполирования назад.
Лекция 6
Классификация уравнений. Этапы численного решения. Любое уравнение может быть записано в следующем общем виде f(x)=0. Если f(x) – алгебраическая функция (например, f(x)=x4+2x-1, f(x)= a0 xn + a1 xn-1 +…+ an-1x + an=0. (*) Если f(x) не является алгебраической (содержит степенную, логарифмическую, функцию sin, cos и т.д.), то уравнение называют трансцендентным (например, f(x)=2x + lnx - 6). Решить уравнение – это значит найти такие значения x, (которые называют корнями уравнения), при которых заданные уравнения обращается в тождество. При численном приближённом решением уравнения выделяю 2 этапа: 1. отделение корней – отыскание достаточно малых интервалов, в каждом из которых один и только один корень уравнения; 2. вычисление каждого корня с заданной точностью внутри выделенного интервала. Отделение корней. Пусть [a, b] – интервал изменения х, в котором отыскиваются вещественные корни уравнения f(x)=0, где f(x) – непрерывная функция вещественного переменного. Разбив [a, b ] на n отрезков длинной
Алгоритм определения корней можно показать следующей блок схемой (см. лист 9). Алгоритм предусматривает ввод (блок 1) исходных данных (a, b – начало и конец исследуемого интервала, n – число одинаковых отрезков разбития [a, b] на подынтервалы) и определение величины
Если отказаться от блока 10, то при случайном совпадении корня с точкой xk деление отрезка произойдёт выдача на печать значений двух интервалов При определении корней алгебраического уравнения (*) можно воспользоваться следующими закономерностями: а) алгебраические уравнения п – го порядка имеет п корней, среди которых могут быть вещественные и комплексные; b) число положительных вещественных корней равно числу (или меньше на чётное число) перемен законов в последовательности коэффициентов a0, a1 , a2, …, an, причём равные нулю коэффициенты не учитываются (теорема Декарта).
После отделения корней можно приступать к нахождению корня с заданной точностью на каждом выделенном интервале.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.006 с.) |

 =
= 
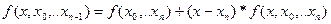
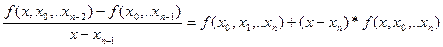
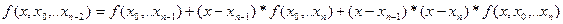



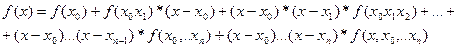
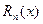
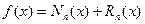
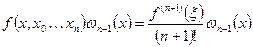
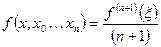
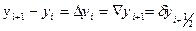 – конечные разности
– конечные разности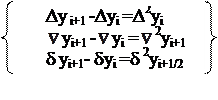
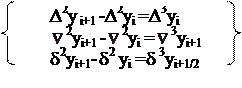


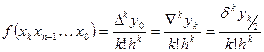
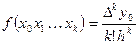 и мы получим полином Ньютона для интерполирования вперед.
и мы получим полином Ньютона для интерполирования вперед.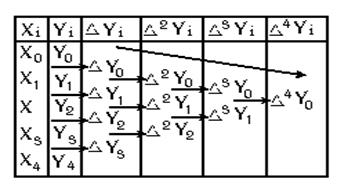
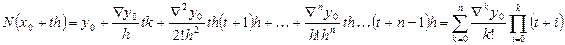 Эта формула применяется при вычислении в начале таблицы разности.
Эта формула применяется при вычислении в начале таблицы разности.
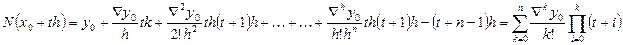 Эта формула применяется для интерполирования в конце таблицы.
Эта формула применяется для интерполирования в конце таблицы. ), то уравнение называют алгебраическим. Всякое алгебраическое уравнение может быть преобразовано к виду
), то уравнение называют алгебраическим. Всякое алгебраическое уравнение может быть преобразовано к виду , наличие простого корня
, наличие простого корня 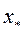 в интервале [xk-1, xk], k=1, 2, …, n, легко установить по знаку произведения концевых значений функции f:
в интервале [xk-1, xk], k=1, 2, …, n, легко установить по знаку произведения концевых значений функции f: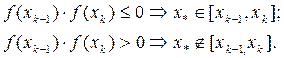
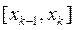 длиной
длиной 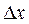 вычисляется
вычисляется  (блок 3) и y=f(xk) (блок 7), а затем, в результате исследования знака произведения
(блок 3) и y=f(xk) (блок 7), а затем, в результате исследования знака произведения 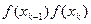 (блок 8), решается вопрос о существовании на
(блок 8), решается вопрос о существовании на 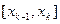 простого корня. При
простого корня. При  предусматривается выдача значений границ
предусматривается выдача значений границ 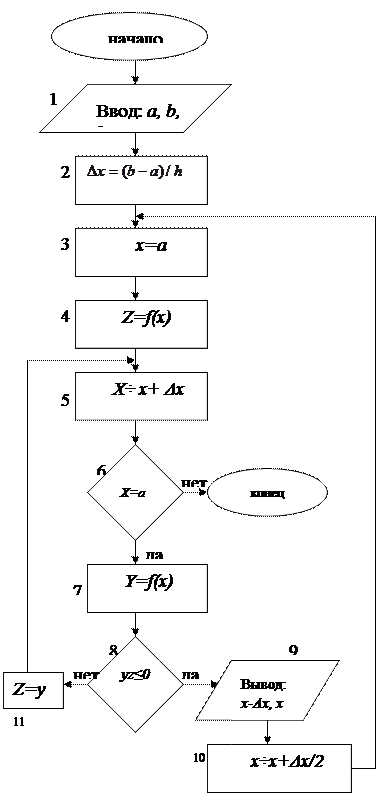
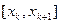 , хотя нам достаточно одного.
, хотя нам достаточно одного.


