
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и относительная погрешность.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть α- точное значение некоторой величины, αn- известное приближенное к этому точному значению. Абсолютной погрешностью приближения α называется величина
Абсолютная погрешность далеко не всегда может охарактеризовать эффективность метода получения приближённого результата: например ∆α= 1 мм при измерении расстояния в 1 км или диаметра вала 4 мм, имеют совершенно различную характеристику качества измерения. Поэтому часто пользуются относительной погрешностью
Часто используют относительную погрешность выраженную в %. Погрешность арифметической операции Арифметические действия над приближенными числами приводят к накоплению погрешности результата решения математической задачи. Пусть α, в, αn и вn – некоторые числа и их приближенные значения, α◦в- некоторая арифметическая операция над числами. Тогда абсолютную и относительную погрешности арифметических операций будем записывать в виде
При этом если ∆α >0 и ∆b>0, то
Используя данные результаты можно оценить и относительные погрешности
δ(αn)=nδα При оценке погрешности вычисления функций y=f(x) для придельных значений абсолютных и относительных погрешностей используем равенства
где xn- приближённое значение величин х, ∆x- придельная погрешность. Алгоритмы являются строгим описанием последовательности операций. Общие свойства алгоритмов: 1) Массовость- применимость ко всем задачам рассматриваемого класса при любых исходных данных или с оговариваемыми границами их изменения. 2) Определенность- любой шаг алгоритма не должен допускать толкования. 3) Дискретность- представимость всякого процесса в виде последовательности выполняемых друг за другом отдельных законченных шагов. 4) Результативность- получение результата за конечное число действий, причем с требуемой точностью. Лекция 2 Общие понятия об интерполировании. Рассмотрим следующую задачу. Пусть функция f(x) задана таблично, т. е. известны её значения в (n+1) – точках xi Є[a,в], где i=0,1,2…n f(xi) =yi
Точки x0x1x2…xn называются узлами интерполяции. Требуется найти простую функцию φ(х), что φ(xi)= f(xi) в узлах интерполяции и φ(x)≈ f(x) в остальных точках х. Пусть Обобщенный полином называют интерполяционным, если f(xi)= φ(xi) i=0,1,2… в узлах интерполяции. Обычно в качестве {φi(x)} берутся функции. 1) 1, х, х2, х3… 2) 1, sinx, cosx, sin2x, cos2x… 3) 1, eλ1х, eλ2х, eλ3х… λ1 λ2 …λn- некоторая последовательность. Линейная интерполяция. При линейной интерполяции предполагается, что функция f(x) между узлами интерполяции изменяется по линейному закону (см. рис)
из геометрии уравнение прямой, проходящей через точки (xi-1 yi-1) и (xi yi) будет иметь вид ( Отсюда для каждого x, лежащего в интервале [xi-1 xi ] может быть найдено соответствующее значение y по формуле
Таким образом, мы можем найти любое f(x) =y на любом отрезке интерполяции. Интерполяционный многочлен Лагранжа. Точность аппроксимации можно повысить, если вместо линейной функции использовать алгебраический многочлен Ln(x)= a0+ a1x+a2x2+…+ anxn Будем искать его в виде.
где φj (x) – многочлен n, который удовлетворяет условия
В n точках полином обращается в нуль и только в одной точке i=j обращается в 1. Раз он обращается в нуль в n точках, то в нем должен быть множитель φj (x)=Сj (x-x0)(x-x1 )…(x-xj-1)(x-xj+1 )… (x-xn) (2) где Сj – неопределенный коэффициент. Надо потребовать, чтобы в точке i=j он обратился в 1
1=φj (xj)=Сj (x-x0)(x-x1 )…(x-xj-1)(x-xj+1 )…(x-xn) и тогда
Или подставляя (3)→(2) получим
Подставляя (4) в (1) получим
Lj (n)(x) Полученный полином называют интерполяционным полиномом Лагранжа. Если ввести обозначение ωn+1(x)= (x-x0)(x-x1)… (x-xn), то полином Лагранжа заменяется в виде:
Lj (n)(x)
Тогда φj (x) и Lj (n)(x) называются Лагранжевыми коэффициентами. Составление полинома Лагранжа и вычисление его в отдельных точках в ручную довольно таки трудоемкая задача. Добавление лишнего узла приводит к пересчету всех коэффициентов. Остаточный член интерполяционной формулы Лагранжа выглядит так
Тогда f(x)= Ln(x)+ Rn(x)
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 или αn= α ± ∆α
или αn= α ± ∆α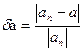 или
или 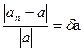













 -последовательность вещественных функций. Тогда
-последовательность вещественных функций. Тогда  называется обобщенным полиномом.
называется обобщенным полиномом.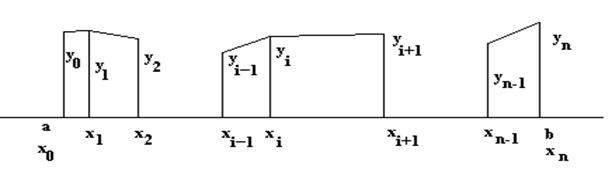

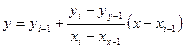
 (1)
(1)
 (3)
(3) (4)
(4)
 (5)
(5)
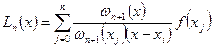 (6)
(6) (7)
(7)


