Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение. Численные методы и приближённые вычисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лекция 1
Введение. Численные методы и приближённые вычисления Раздел математики, занимающийся построением и обоснованием численных алгоритмов, решений сложных задач из различных областей науки и производственной деятельности называется прикладной математикой. Главная задача прикладной математики нахождение решений с требующейся точностью. Этим она отличается от классической математики, которая основное внимание уделяет исследованию условий существования решений и его свойств. В истории прикладной математики можно различить 3 периода: 1 период 3-4 тыс. лет назад – вычисление объемов, площадей и решение простых задач арифметики, алгебры, геометрии. (жрецы) 2 период начался с Ньютона. Решались задачи астрономии, геодезии и расчета механических конструкций. Задачи сводились либо к решению ОДУ, либо систем линейных алгебраических уравнений (СЛАУ). Бруно, Коперник. 3 период начался с 1940 года, когда надо было быстро рассчитывать, быстро передвигаться, предметы (катюша), зенитные орудия и т.д. Курчатов, Сахаров, Королев, Появились ЭВМ. Это потребовало от исследователей разработки и совершенствования ранее существующих методов и разработки новых методов. Не следует думать, что знание численных методов и новых ЭВМ позволяет сразу решить любую задачу. Решение сложной инженерной задачи выполняется в следующей последовательности.
Система отношений, связывающая исходные и конечные параметры. Позволяет по исходным данным найти исходный результат. Составляется схема последовательных действий (алгоритм).
Тот же алгоритм, но записанный на языке «понятном» для ЭВМ.
При построении математической модели могут быть упущены или некорректно учтены некоторые важные обстоятельства. Выбранный метод решения может дать недопустимо грубый результат. При составление алгоритма или программы могут быть допущены различного рода ошибки. И если инженер является узким специалистом только в своей области специальных знаний, то он полностью зависит от математика и программиста. Знание курса вычислительной математики позволяет избавиться от этой зависимости.
Раздел вычислительной математики состоит из следующих частей: 1) Общие понятия об интерполировании функции. Численное интегрирование и дифференцирование. 2) Решение СЛАУ. 3) Решение нелинейных уравнений. 4) ОДУ. 5) Задачи на собственные решения. Методы решения Методы решения задач делятся на аналитические, графические и численные. Численные методы- это методы приближенного или точного решения математической задачи, основанные на построении конечной последовательности арифметических действий над числами. Численные методы связанны, прежде всего, с погрешностями при работе с числовой информацией. Абсолютная и относительная погрешность. Пусть α- точное значение некоторой величины, αn- известное приближенное к этому точному значению. Абсолютной погрешностью приближения α называется величина
Абсолютная погрешность далеко не всегда может охарактеризовать эффективность метода получения приближённого результата: например ∆α= 1 мм при измерении расстояния в 1 км или диаметра вала 4 мм, имеют совершенно различную характеристику качества измерения. Поэтому часто пользуются относительной погрешностью
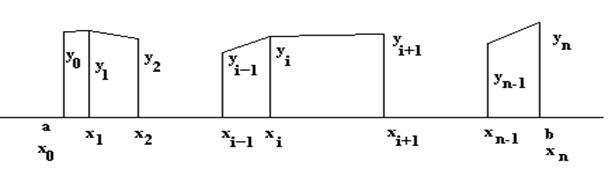
Часто используют относительную погрешность выраженную в %. Лекция 2 Линейная интерполяция. При линейной интерполяции предполагается, что функция f(x) между узлами интерполяции изменяется по линейному закону (см. рис)
из геометрии уравнение прямой, проходящей через точки (xi-1 yi-1) и (xi yi) будет иметь вид ( Отсюда для каждого x, лежащего в интервале [xi-1 xi ] может быть найдено соответствующее значение y по формуле
Таким образом, мы можем найти любое f(x) =y на любом отрезке интерполяции. Лекция 3
Методы приближенного интегрирования. Формулы Ньютона –Котеса. Один из методов приближенного интегрирования
В этом случае, если взять узлы интерполяции равноотстоящими, то xk=x0+k*h k=0,1,2…n x=x0+t*h dx=hdt
x-x1=(x0+th)-(x0+1h)=(t-1)h _ _ _ _ _ _ a=x0=x0+th x-xn=(x0+th)-(x0+nh)=(t-n)h
xk-x0=(x0+kh)-(x0+0h)=kh _ _ _ _ _ b=xn=x0+nh=x0+nh
_ _ _ _ _ _
Частные случаи. n=1 L1(x)=ax+ b
A1(0)=- A1(1)=
n=2 L2(x)=a2 x+ b+c
A2(0)=- A2(1)= A2(2)=
Лекция 4
Лекция 5
Разделённые разности
Пусть функция f(x) вычислена в точках
Разность вида: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Разность вида:
т. е. узлы можно менять любым образом. 2) Разделённые разности порядка k от
3) Линейность разделённой разности относительно функции, к которой применяется разделённая разность.
Конечные разности. В случаях когда узлы интерполяции берутся равноотстоящими xk=x0+k*h k=0,1,2…n n- шаг интерполирования, то часто вводят следующие обозначения
0нисходящие восходящие - конечная разность 2 го порядка центральные
- конечная разность 3 го порядка
Лекция 6
Отделение корней. Пусть [a, b] – интервал изменения х, в котором отыскиваются вещественные корни уравнения f(x)=0, где f(x) – непрерывная функция вещественного переменного. Разбив [a, b ] на n отрезков длинной
Алгоритм определения корней можно показать следующей блок схемой (см. лист 9). Алгоритм предусматривает ввод (блок 1) исходных данных (a, b – начало и конец исследуемого интервала, n – число одинаковых отрезков разбития [a, b] на подынтервалы) и определение величины
Если отказаться от блока 10, то при случайном совпадении корня с точкой xk деление отрезка произойдёт выдача на печать значений двух интервалов При определении корней алгебраического уравнения (*) можно воспользоваться следующими закономерностями: а) алгебраические уравнения п – го порядка имеет п корней, среди которых могут быть вещественные и комплексные; b) число положительных вещественных корней равно числу (или меньше на чётное число) перемен законов в последовательности коэффициентов a0, a1 , a2, …, an, причём равные нулю коэффициенты не учитываются (теорема Декарта).
После отделения корней можно приступать к нахождению корня с заданной точностью на каждом выделенном интервале. Метод итераций. Приведём уравнение Возьмём некоторую произвольную точку
При этом
Необходимо отметить, что последовательность { Линейное уравнение Взяв за начальное приближение
Данная последовательность стремится к точному решению уравнения. Во втором случае
Эта последовательность расходится. Следовательно, вид функции Сходимость метода простой итерации определяется следующей теоремой: При любом начальном приближении
с постоянной Липшица Если функция В рассмотренных выше примерах для уравнения Для уравнения Если вычисление постоянной Липшица сопряжено с определёнными математическими трудностями, то алгоритм метода простой итерации использует косвенную оценку точности вычислений
где Блок – схема алгоритма метода простой итерации с косвенной оценкой точности вычислений:
Лекция 7
Численные решения СЛАУ. Метод Гаусса. Пусть задана система линейных уравнений Ax=U с плотной матрицей, элементы которой хранятся в оперативной памяти.
Переходим к системе (исключения х1)
Эта операция равносильна умножению Ax=U слева на матрицу
где pi1= aij(1)= aij- Следующий переход к системе (исключения х2)
Это исключения равносильно умножению A1 x= U 1 слева на матрицу Р2:
где pi2= A1 x= U1=> Продолжая этот процесс и так далее, мы придем к легко решаемой системе уравнений с треугольной матрицей An-1х =Un-1
P Q
Где матрица P- нижняя треугольная, а Q- верхняя треугольная. Решение по методу Гаусса сводится к разложению A на произведение двух треугольных матриц. Одна из них
Заметим, что det A=det P*det Q= a11 a22(1) a33(2)… ann(n-1)
Py= U ↓ (y)
Qx= y ↑ (x) Решения по методу Гаусса сводится фактически к решению системы Py= U ↓ При прямом ходе, а затем к решению системы Qx= y ↑ при обратном ходе.
После вычисления прямого хода мы получаем матрицу An-1= Q Метод Холецкого, прогонки приводят к факторизации матрицы A. Метод Холецкого. Пусть дана невырожденная матрица размером N*N (det A≠0) Представим её в виде произведения
k>i bik=0, когда k>i ckj=0 при k>j cjj =1 Из (1) следует aij= Преобразуем эту сумму двумя способами aij=
aij= Отсюда находим bij= cjj= Матрицы B и C найдены, тогда Ax= BCx=U By=U ↓ (y) прямой ход
Cx=y ↑ (x) обратный ход
Лекция 8 Метод прогонки. Решение многих задач для обыкновенных дифференциальных уравнений и уравнений в частных производных приводит к системам линейных уравнений с матрицами специального вида, для решения которых целесообразно применять не общие методы, а методы, использующие специфику полученной системы. Пусть требуется найти решение следующей системы трехточенных уравнений.
Или в векторной форме A
A=
По методу Гаусса A= * = * Факторизация ленточных матриц, т.е. разложение их на произведение двух треугольных матриц A=PQ (нижней и верхней) треугольных матриц может быть произведено так, что P и Q также будут ленточными матрицами. Перейдем к следующей системе (3) yj=pj+1yj+1+qj+1 (3) Где pj+1 и qj+1 неизвестные числа
u1- p2u2 =q2 = u0- p1u1 =q3
Числа pj и qj можно искать из системы (1), т.к. yj-1=pjyj+qj (4) Подставляя (4) в систему (1) получим -aj(pj yj+ qj)+cj yj-bj yj+1=fj (cj-aj pj)yj=bj yj+1 +(fj+ aj qj)
Сравнивая (5) с(3) получим
Из 1 го крайнего условия
Из 2 го крайнего условия
-an yn-1+cnyn=fn
Теперь с помощью (3) получим
Проверка метода прогонки на устойчивость. Поскольку вычисления pj и qj производятся по рекуррентным формулам, то в зависимости от элементов матрицы A: ai, bi, ci, то неизбежны ошибки округления при вычислении по рекуррентным формулам pj и qj. Эти ошибки могут быстро возрастать и сделать вычисления непригодными. Поведение ошибки dpj+1 можно проследить, положив её приближённо равной дифференциалу функции.
Имеем
Прогонка будет устойчивой, если Тогда dpj+1 <dpj Эти неравенства (10) будут выполнены, если, например, положить, что коэффициент матрицы A удовлетворяют следующие условия
0≤ aj≤bj cj≥ aj+bj (11) j= 0< В самом деле
Вообще, проверяется pj+1≤ 1 для j=1,n-1 При этих условиях при вычислении pj+1 накопление ошибки не происходит. Аналогично из равенств
Т.к. при тех же условиях (11) нарастания погрешностей при вычислении q j+1 не происходит.
Лекция 9 Лекция 10
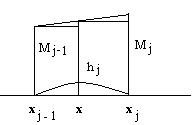
Сплайны. Пусть есть функция f(x) заданная в узлах отрезка [a,b]. Пусть заданны узлы интерполяции x0x1…xn xi Будем приближать функцию f(x) на каждом отрезке ∆~[xj-1xj] полиномом Pj,m(x)=a0j+a1jx+…+ anjxm Сплайном назовем S∆(x) функцию совпадающую на каждом участке [xj-1xj] с полиномом Pj,m(x) и такую, что во всех внутренних узлах непрерывную вместе со своими производными до (m-1) порядка включительно во всех точках xi i=1, n-1. Кубический сплайн. Будем считать, что на каждом участке [xj-1xj] мы приближаем полином 3=ей степени. Pj,3(x)=ax3+bx2+cx+d, тогда
Найдем S∆(x) для чего проинтегрируем дважды (1), получим
Найдем с1 и с2 из условия S∆(xj-1)= y j-1 S∆(xj)= y j
C1hj=yj- Mj C1= C2=
Поскольку S∆`(xj-0)= S∆(xj+0)
Приравнивая получаем
λj= μiMj-1+2Mj+ λj Mj=dj j=1,n-1 Полученная система служит для определения M0 M1… Mn, подставляя в формулы (х) и (х*) получим, что полином удовлетворяет 3-м свойствам 1) S∆(xj-0)= S(xj+0) 2) S`(xj-0)= S` (xj+0) 3) S``(xj-0)= S``(xj+0)
Лекция 11 Метод простой итерации. Пусть задана система линейных уравнений Ax=b=>Ax-b=0 (1) Ax`-b=ξ- невязка x- x+ Ax-b=0=>x= (I-A) x+ b=>x=Bx+ b (2) Пусть матрица B невырожденная, т.е. det B≠0/ Выбрав произвольно x0 вычисляем последовательно xk xk= Bxk-1+b (3) Пусть x*- точное решение уравнения (1) и (2), тогда
(xk-x*) =B (xk-1-x*) (4) (xk-x*) =B (xk-1-x*) = B B (xk-2-x*) = Bk (x0-x*) (4a) Пронормируем последнее выражение (4а) получим:
Из полученного неравенства следует, что при произвольном выборе x0 соотношение Эквивалентно Лекция 12 Метод Зейделя. Решение системы Ax=U по методу Зейделя производится по формулам
Если при вычислении i-той координаты вектора
То вычисления будут проходить по формулам Зейделя. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |




 Формулируется конечная цель решения, выявляются исходные и получаемые параметры.
Формулируется конечная цель решения, выявляются исходные и получаемые параметры.
 или αn= α ± ∆α
или αn= α ± ∆α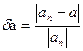 или
или 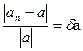

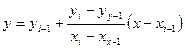

 f(x)d(x) заключается в замене функции f(x) на какой- либо интерполяционный полином. Например
f(x)d(x) заключается в замене функции f(x) на какой- либо интерполяционный полином. Например

 x-x0=(x0+th)-(x0+0h)=th
x-x0=(x0+th)-(x0+0h)=th t=0
t=0 xk-xk-1=(x0+kh)-(x0+(k-1)h)=1h
xk-xk-1=(x0+kh)-(x0+(k-1)h)=1h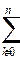
 dt*
dt* 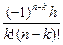 f(xk)=
f(xk)= 
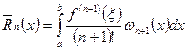
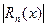
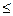

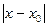
 …
…  dx=
dx= 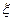
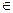 [a, b]
[a, b]
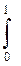
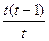 dt=
dt= 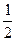
 dt=
dt= 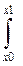 f(x)dx=h(
f(x)dx=h(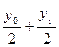 )=
)= 
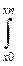 f(x)dx=
f(x)dx= 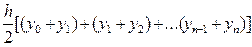 = h[
= h[ 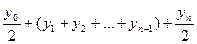 ]
]
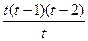 dt=
dt= 
 dt=
dt= 
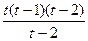 dt=
dt=  f(x)dx=h(
f(x)dx=h(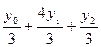 )=
)= 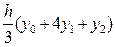
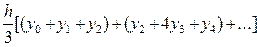 = =
= = 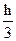 [
[ 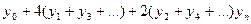 ]
] i=0,1,2,…,n,
i=0,1,2,…,n, 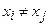 . Тогда выражение
. Тогда выражение называется разделённой разностью 1-го порядка.
называется разделённой разностью 1-го порядка. называется разделённой разностью 2-го порядка
называется разделённой разностью 2-го порядка -называется разделённой разностью к-го порядка. Вычисляются разделённые разности согласно Таблицы №1.
-называется разделённой разностью к-го порядка. Вычисляются разделённые разности согласно Таблицы №1.


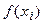
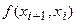



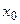
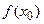
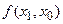
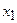



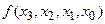



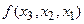

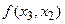



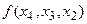
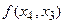



 1) Разделённые разности симметричны относительно своих аргументов
1) Разделённые разности симметричны относительно своих аргументов 
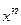 являются однородным многочленом относительно своих аргументов степени n-k, при n=k она равна 1, а при k>n она равна 0.
являются однородным многочленом относительно своих аргументов степени n-k, при n=k она равна 1, а при k>n она равна 0.
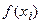







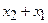

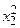



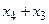

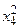
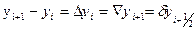 – конечные разности
– конечные разности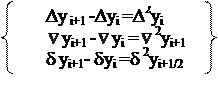
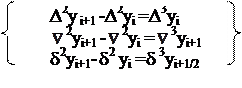
 , наличие простого корня
, наличие простого корня 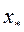 в интервале [xk-1, xk], k=1, 2, …, n, легко установить по знаку произведения концевых значений функции f:
в интервале [xk-1, xk], k=1, 2, …, n, легко установить по знаку произведения концевых значений функции f: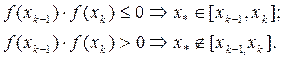
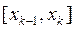 длиной
длиной 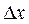 вычисляется
вычисляется  (блок 3) и y=f(xk) (блок 7), а затем, в результате исследования знака произведения
(блок 3) и y=f(xk) (блок 7), а затем, в результате исследования знака произведения 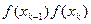 (блок 8), решается вопрос о существовании на
(блок 8), решается вопрос о существовании на 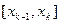 простого корня. При
простого корня. При  предусматривается выдача значений границ
предусматривается выдача значений границ 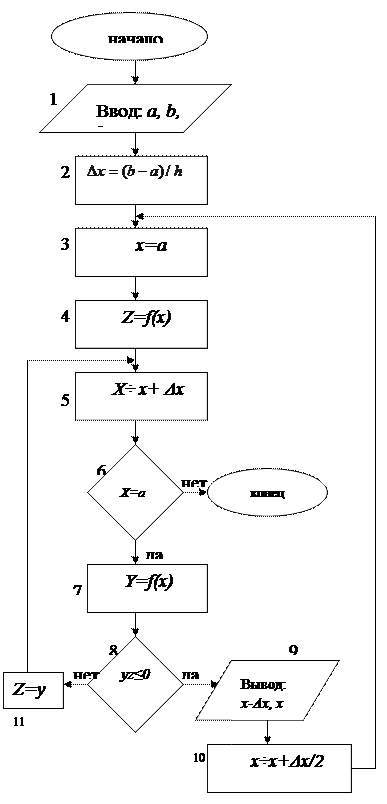
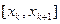 , хотя нам достаточно одного.
, хотя нам достаточно одного.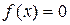 к виду
к виду  (1)
(1)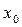 на оси
на оси  . Если существует такая точка
. Если существует такая точка 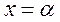 , что
, что 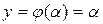 , то очевидно, число
, то очевидно, число 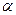 и будет корнем уравнения (1). В общем случае
и будет корнем уравнения (1). В общем случае  . Суть метода простых итераций (повторений) состоит в построении последовательности {
. Суть метода простых итераций (повторений) состоит в построении последовательности {  } точек, сходящихся к корню
} точек, сходящихся к корню 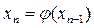 ,
,  (2)
(2) называют начальным приближением.
называют начальным приближением.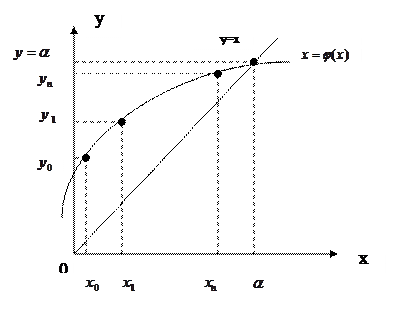
 } не всегда является сходящейся. Рассмотрим пример:
} не всегда является сходящейся. Рассмотрим пример: , имеющее корень
, имеющее корень  можно преобразовать к виду
можно преобразовать к виду  или
или  .
.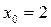 , в первом случае получим
, в первом случае получим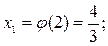
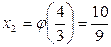 ;
;  , …
, …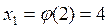 ;
; 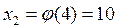 ;
;  , …
, … оказывает существенное влияние на сходимость итерационного процесса.
оказывает существенное влияние на сходимость итерационного процесса.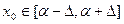 на некотором интервале последовательность
на некотором интервале последовательность  , построенная в соответствии с методом простой итерации (2), сходится к корню
, построенная в соответствии с методом простой итерации (2), сходится к корню  , который является единственным решением уравнения (1) на рассматриваемом интервале, если здесь функция
, который является единственным решением уравнения (1) на рассматриваемом интервале, если здесь функция 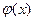 удовлетворяет условию Липшица
удовлетворяет условию Липшица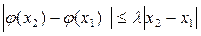
 .
.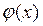 дифференцируема и имеет на
дифференцируема и имеет на  ограниченную производную, то постоянная Липшица
ограниченную производную, то постоянная Липшица  .
.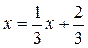
 и итерационный процесс является сходящимся к корням уравнения
и итерационный процесс является сходящимся к корням уравнения 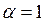 .
.
 и условия сходимости не выполняется.
и условия сходимости не выполняется. ,
, - допустимая погрешность вычислений.
- допустимая погрешность вычислений.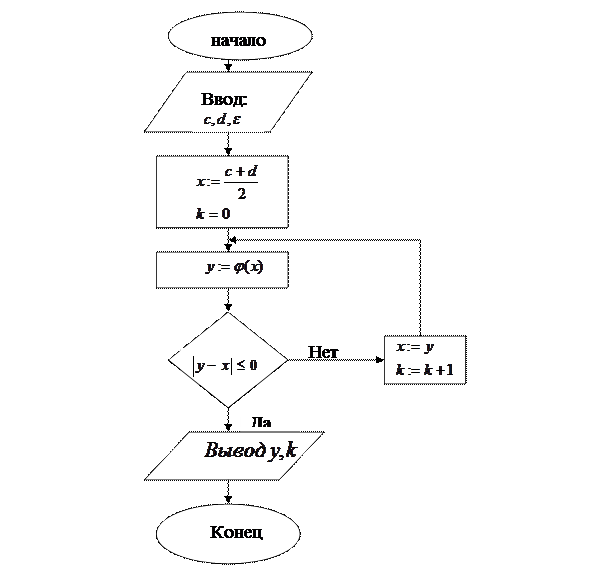
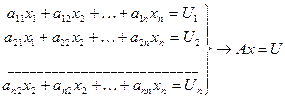
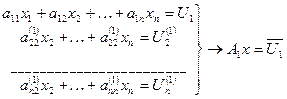
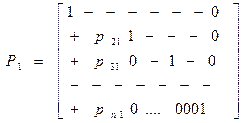
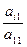 i=2,3…n A1 x= U1à
i=2,3…n A1 x= U1à 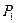 Ax=
Ax= 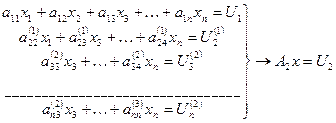
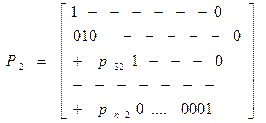
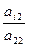 i=3,4…n aij(2)= aij(1) -
i=3,4…n aij(2)= aij(1) - 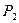 a2j(1)
a2j(1)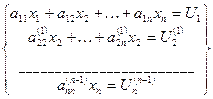
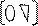 An-1 =
An-1 =
 An-1- верхняя треугольная матрица. Здесь An-1х=Un-1=> =Pn-1Pn-2Ax= Pn-1Pn-2 U, так что A =(Pn-1Pn-2 …P1)-1 An-1х
An-1- верхняя треугольная матрица. Здесь An-1х=Un-1=> =Pn-1Pn-2Ax= Pn-1Pn-2 U, так что A =(Pn-1Pn-2 …P1)-1 An-1х

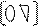
 A = *
A = *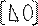 P~ с единицами по главной диагонали и на верхнюю треугольную
P~ с единицами по главной диагонали и на верхнюю треугольную Q~
Q~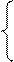
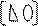 Если представления матрицы A в виде PQ найдены, то решение системы Ax=U сводится к решению двух треугольных систем уравнений.
Если представления матрицы A в виде PQ найдены, то решение системы Ax=U сводится к решению двух треугольных систем уравнений.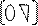 Ax=U=>PQx=U=>
Ax=U=>PQx=U=>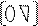
 A=BC (1) A~(aij) B~(bij) C~(cij)
A=BC (1) A~(aij) B~(bij) C~(cij)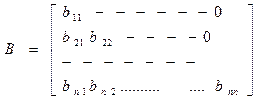

 bik cki
bik cki bik cki+ bii cij+
bik cki+ bii cij+ 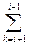 bik cki+ bii cij
bik cki+ bii cij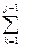 bik ckj+ bij cjj+
bik ckj+ bij cjj+ 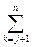 bik ckj=
bik ckj= 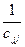
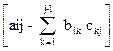 i ≥ j b11=a11 cjj=1
i ≥ j b11=a11 cjj=1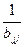
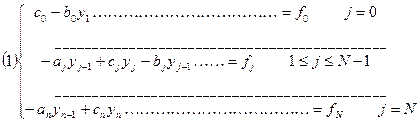
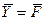 (2)
(2)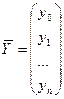
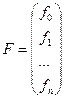
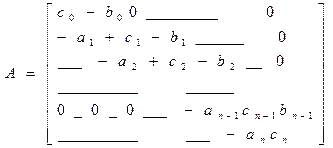

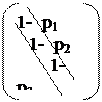

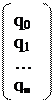
 u0- p1u1 =q1
u0- p1u1 =q1  (5)
(5)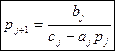
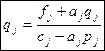 (6)
(6)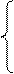
 y0 =p1y1+q1
y0 =p1y1+q1 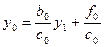 =>
=> 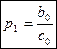
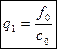 (7)
(7)
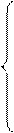 yn-1= pnyn+qn
yn-1= pnyn+qn 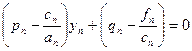
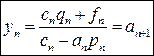 (8)
(8)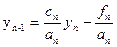
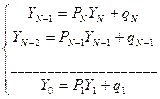
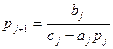
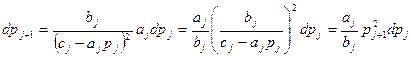 (9)
(9) и
и 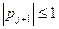 (10)
(10)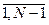
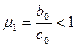
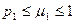 , отсюда
, отсюда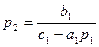 <
< 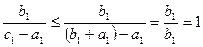
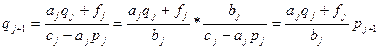 ;
;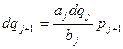 <dqj
<dqj
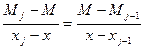
 (1)
(1) 

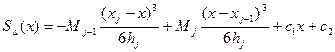

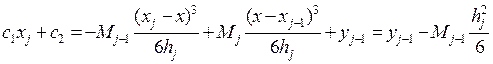
 => C1hj=yj-yj-1+
=> C1hj=yj-yj-1+ 

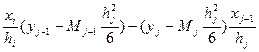
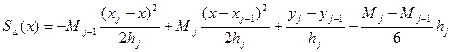

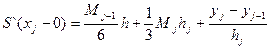
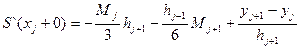
 (2)
(2) μi=
μi= 
 (5)
(5)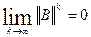 (6) при
(6) при  < 1 (7)
< 1 (7)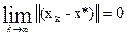 или
или  . Соотношение (6) возможно, если выполнено неравенство (7).
. Соотношение (6) возможно, если выполнено неравенство (7). 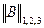 < 1
< 1

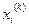 учитывается найденные заранее уже координаты
учитывается найденные заранее уже координаты 
 …
…