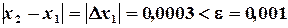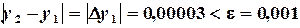Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение нелинейных уравнений.Содержание книги Поиск на нашем сайте
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика»
ЧИСЛЕННЫЕ МЕТОДЫ
ЧАСТЬ 1
Казань
УДК 621.313: 518.6
Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев.
Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика». Численные методы. Часть 1. / Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. Казань, 2011. – 32 с.
Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы решения нелинейных уравнений, систем линейных и нелинейных уравнений.
Рецензент – Р.Б.Салимов, доктор физ.-мат. наук, профессор
Казанский государственный ã архитектурно-строительный университет, 2011г. Метод простой итерации. Для использования этого метода исходное нелинейное уравнение В качестве
Если известно начальное приближение корня Далее подставляя каждый раз новое значение корня в уравнение
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е. Геометрическая интерпретация метода простой итерации. Построим графики функций
Пример 1.4. Решить уравнение Решение. Из условия сходимости (1.5) Подставляя каждый раз новое значение корня в уравнение
получаем последовательность значений:
Теперь На рис.1.10 приведена программа решения данного уравнения методом простой итерации. В качестве исходных данных вводятся начальное приближение, точность вычисления и значение постоянной М.
Пример 1.4. Решить уравнение
Порядок решения (рис. 1.11). 1) Ввести в ячейки A1:D1 заголовки столбцов. 2) В ячейку A2 – значение начального приближения 3) В ячейку B3 – формулу функции =A2^3+A2-1 4) В ячейку C2 – значение M 5 5) В ячейку A3 – формулу первого приближения =A2-B3/$C$2 6) В ячейку D3 – погрешность =ABS(A3-A2) 7) Выделить ячейки A3:D3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:D4, A5:D5, и т.д. при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения. 8) В столбце A найти значение корня, соответствующее заданной точности. Приближенное решение данного уравнения Метод Гаусса. Этот метод является одним из наиболее распространенных прямых методов решения систем линейных алгебраических уравнений. В основе метода Гаусса лежит идея последовательного исключения неизвестных. Рассмотрим систему из трех уравнений с тремя неизвестными:
Система уравнений (2.2) приводится к эквивалентной системе с треугольной матрицей:
Достигается это при помощи цепочки элементарных преобразований, при которых из каждой строки вычитаются некоторые кратные величины, расположенные выше строк. Процесс приведения системы (2.2) к системе (2.3) называется прямым ходом, а нахождение неизвестных Прямой ход исключения: Исключаем В результате получаем следующую систему:
Из полученной системы (2.4) исключаем
Взяв из каждой системы (2.2), (2.4) и (2.5) первые уравнения, получим систему уравнений с треугольной матрицей. Обратный ход: Из уравнения (III²) находим Аналогичным путем методом Гаусса решаются системы Пример 2.1. Решить систему уравнений методом Гаусса:
Решение: Удалить члены с
2-я строка делится на
2-я строка умножается на
3-я строка делится на
Процедура обратного хода дает исходное решение:
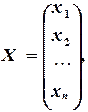
Метод обратной матрицы. Систему (2.1) можно представить в матричном виде как
где Решение можно выразить, используя умножение на матрицу
Пример 2.2. Решить систему уравнений методом обратной матрицы с помощью программы Excel:
Порядок решения. 1) Ввести матрицу 2) Выделить ячейки для хранения обратной матрицы 3) Вызвать мастер функций, в категории «Математические» выбрать функцию вычисления обратной матрицы МОБР. В диалоговом окне аргументов функции заполнить поле ввода «Массив» - указать диапазон ячеек матрицы 4) Чтобы получить всю обратную матрицу, нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В ячейках A8:D11 появятся значения обратной матрицы 5) Выделить ячейки для хранения вектора-столбца 6) Вызвать мастер функций, в категории «Математические» выбрать функцию матричного умножения МУМНОЖ. В диалоговом окне аргументов функции в поле ввода «Массив1» указать диапазон ячеек матрицы 7) Чтобы получить весь вектор
Метод прогонки. Применяется для решения систем уравнений с трехдиагональной (ленточной) матрицей. Такая система уравнений записывается в виде:
Является частным случаем метода Гаусса и состоит из прямого и обратного хода. Прямой ход состоит в исключении элементов матрицы системы (2.6), лежащих ниже главной диагонали. В каждом уравнении останется не более двух неизвестных и формулу обратного хода можно записать в следующем виде:
Уменьшим в формуле (2.7) индекс на единицу:
Выразим
Сравнивая (2.7) и (2.8), получим:
Поскольку
Теперь по формулам (2.9) и (2.10) можно вычислить прогоночные коэффициенты
Пример 2.3. Решить систему уравнений методом прогонки:
Решение. Коэффициенты записываем в виде таблицы 2.1.
Прямой ход прогонки. По формулам (2.9) и (2.10) определяем прогоночные коэффициенты
Обратный ход прогонки. По формулам (2.7) вычисляем все Далее вычисляем:
Вычисляем невязки
Алгоритм метода прогонки: 1. Ввести число уравнений 2. Ввести 3. Вычислить 4. Вычислить 5. Вычислить невязки 6. Напечатать
На рис. 2.2 приведена программа решения методом прогонки. CLC INPUT N DIM A(N),B(N),C(N),D(N),U(N),V(N),X(N+1),R(N) FOR I=1 TO N INPUT A(I),B(I),C(I),D(I) U(I)=-C(I)/(A(I)*U(I-1)+B(I)) V(I)=(D(I)-A(I)*V(I-1))/(A(I)*U(I-1)+B(I)) NEXT I FOR I=N TO 1 STEP -1 X(I)=U(I)*X(I+1)+V(I) NEXT I FOR I=1 TO N R(I)=D(I)-A(I)*X(I-1)-B(I)*X(I)-C(I)*X(I+1) PRINT ²X²;I; ²=²; X(I), ²R²; I; ²=²; R(I) NEXT I Рис.2.2. Программа решения системы линейных алгебраических уравнений методом прогонки на языке QUICK BASIC.
Пример 2.4. Решить систему уравнений из примера (2.3) методом прогонки с помощью программы Excel. Порядок решения. 1) Ввести в ячейки A1:G1 заголовки столбцов (рис. 2.3). 2) В ячейки A3:D6 – коэффициенты 3) В ячейку E3 – формулу 4) В ячейку F3 – формулу 5) В ячейку G3 – формулу 6) Выделить ячейки E3:G3 и скопировать формулы в соседние ячейки E4:G4 … E6:G6 при помощи маркера заполнения. 7) В ячейках G3:G6 появятся значения решения системы уравнений.
Порядок решения. 1) Представить систему в виде (2.16); 2) Ввести в ячейки A1:G1, D2:G2 заголовки столбцов (рис. 2.4); 3) В ячейки A2:C2 – начальное приближение 0, 0, 0; 4) В ячейку A3 – формулу 5) В ячейку B3 – формулу 6) В ячейку C3 – формулу 7) В ячейку D3 – формулу погрешности 8) Выделить ячейку D3 и скопировать формулу в соседние ячейки E3:F3 при помощи маркера заполнения; 9) В ячейку G3 – формулу максимальной погрешности =МАКС(D3:F3) 10) Выделить ячейки A3:G3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:G4, A5:G5 и т.д.при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения; 11) Ячейки A15, B15, C15 содержат решение системы уравнений, соответствующее заданной точности (G15).
Приближенное решение системы с точностью
Метод Зейделя. Вычисления в этом методе почти такие же, как и в методе Якоби, с той лишь разницей, что в последнем новые значения
Сходимость и точность достигаются условиями (2.13) и (2.14).
Пример 2.7. Задать итерационный процесс Зейделя для нахождения решений системы уравнений (2.15). Решение. Достаточное условие сходимости (2.13) выполняется, поэтому начальное приближение может быть любым. Используя (2.16) получим:
После задания начального приближения, например,
Результаты первой итерации подставляют в правую часть и получают результаты второй итерации:
Результаты второй итерации подставляют в правую часть и получают результаты третьей итерации:
Погрешность решения:
Метод Зейделя. Метод Зейделя отличается от метода Якоби тем, что вычисления ведутся не по формулам (3.4), а по следующим формулам:
…
При решении систем нелинейных уравнений необходимо определить приемлемое начальное приближение. Для случая двух уравнений с двумя неизвестными начальное приближение находится графически. Сходимость метода Зейделя (Якоби тоже) зависит от вида функции в (3.2), вернее она зависит от матрицы, составленной из частных производных:
где Итерационный процесс сходится, если сумма модулей каждой строки
или Пример 3.1. Найти решение системы методом Зейделя с точностью
Решение: Представим (3.8) в виде (3.5):
Задаем начальные приближения Запишем достаточное условие сходимости и определяем
Определяем частныезначения
Переходим к реализации итерационного процесса:
Определяем погрешностьпо формуле
Таким образом, имеем решение: Программа, реализующая решение данной задачи, представлена на рис. 3.1.
Метод Ньютона. Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности систем линейных уравнений. Рассмотрим систему двух нелинейных уравнений с двумя неизвестными вида:
Пусть известно некоторое приближение
Для этого разложим функции
относительно неизвестных поправок Таким образом, решение системы уравнений по методу Ньютона состоит в построении итерационной последовательности:
где В методе Ньютона для обеспечения хорошей сходимости также важен правильный выбор начального приближения. Пример 3.2. Найти решение системы (3.8) методом Ньютона с точностью
Решение. Начальные приближения
и, используя (3.12), построим систему линейных уравнений относительно поправок
Подставляя начальные приближения
определяем поправки на первом шаге итерации
Далее начальное приближение уточняем по формулам (3.13)
Подставляя результаты первой итерации
определяем поправки на втором шаге итерации
Далее
Определяем погрешностьпо формуле
Таким образом, имеем решение: Программа, реализующая метод Ньютона для указанной задачи, представлена на рис. 3.2.
Пример 3.3. Найти решение системы (3.8) с помощью программы Excel.
Порядок решения. 1) Подключить надстройку «Поиск решения» через Главное меню-Сервис-Надстройки (рис. 3.3); 2) Ввести в ячейки A1, B1, C1, D1 заголовки столбцов (рис. 3.4а); 3) В я
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.199.214 (0.009 с.) |

 необходимо привести к виду
необходимо привести к виду 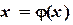 .
.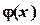 можно принять функцию
можно принять функцию 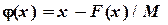 , где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации
, где M ‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации 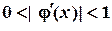 . При этом для определения M условие сходимости записывается в следующем виде:
. При этом для определения M условие сходимости записывается в следующем виде: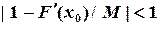 или
или 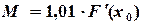 . (1.5)
. (1.5) , подставляя это значение в правую часть уравнения
, подставляя это значение в правую часть уравнения 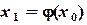 .
. ,
, 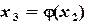 ,...,
,..., 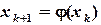 , k = 1,2,...,n.
, k = 1,2,...,n. .
.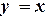 и
и 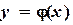 . Корнем
. Корнем 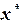 уравнения
уравнения 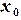 , строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня
, строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня 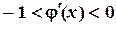 на отрезке
на отрезке 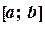 (рис. 1.9а), то последовательные приближения
(рис. 1.9а), то последовательные приближения  (рис. 1.9б), то последовательные приближения сходятся монотонно.
(рис. 1.9б), то последовательные приближения сходятся монотонно.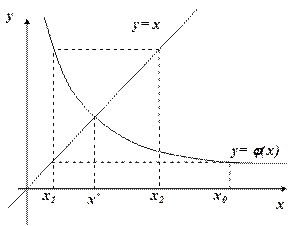

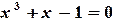 на отрезке
на отрезке 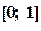 методом простой итерации c точностью
методом простой итерации c точностью 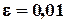 .
. , при
, при 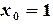 определяем
определяем 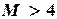 .Пусть
.Пусть 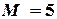 .
.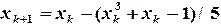 ,
,

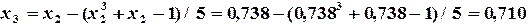
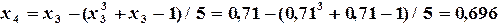
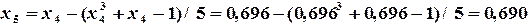
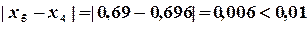 , но
, но 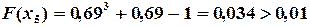 , поэтому продолжаем вычисления.
, поэтому продолжаем вычисления.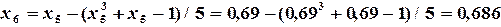
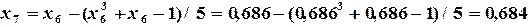
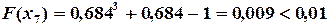 и приближенным решением данного уравнения c точностью
и приближенным решением данного уравнения c точностью 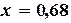 .
.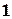
 содержится в ячейке A9 (погрешность
содержится в ячейке A9 (погрешность 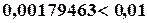 в ячейке D9).
в ячейке D9).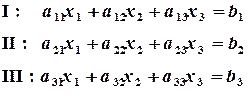 (2.2)
(2.2) (2.3)
(2.3) ,
, 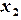 ,
,  из системы (2.3) называется обратным ходом.
из системы (2.3) называется обратным ходом.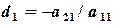 и складываем со вторым, затем умножаем на
и складываем со вторым, затем умножаем на 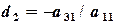 и складываем с третьим.
и складываем с третьим.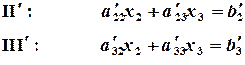 (2.4)
(2.4) и складываем со вторым уравнением, получим уравнение:
и складываем со вторым уравнением, получим уравнение: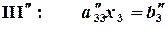 (2.5)
(2.5)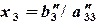 . Из уравнения (II¢) находим
. Из уравнения (II¢) находим 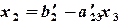 . Из уравнения (I) находим
. Из уравнения (I) находим 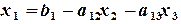 . Коэффициенты
. Коэффициенты  ,
, 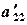 называются ведущими элементами 1-го и 2-го шагов исключения неизвестных. Они должны быть отличны от нуля. Если они равны нулю, то, меняя местами строки, необходимо на их место вывести ненулевые элементы.
называются ведущими элементами 1-го и 2-го шагов исключения неизвестных. Они должны быть отличны от нуля. Если они равны нулю, то, меняя местами строки, необходимо на их место вывести ненулевые элементы. уравнений с
уравнений с 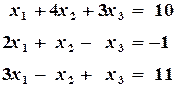
 , а из 3-й - первую, умноженную на
, а из 3-й - первую, умноженную на  :
: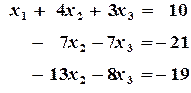
 :
: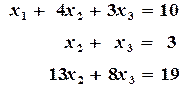
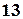 и вычитается из 3-й:
и вычитается из 3-й: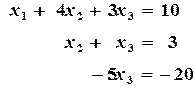
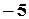 :
: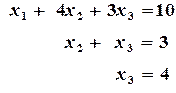
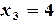 ;
; 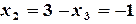 ;
;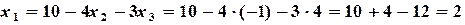
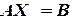 ,
,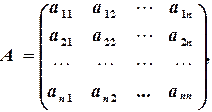
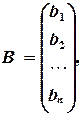
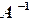 , обратную к
, обратную к 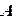 :
: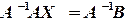
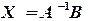
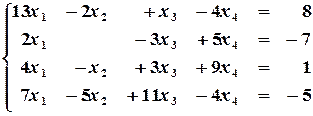
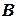 в рабочий лист Excel (рис. 2.1).
в рабочий лист Excel (рис. 2.1).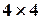 ; например, ячейки A8:D11.
; например, ячейки A8:D11.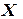
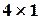 ; например, ячейки F8:F11.
; например, ячейки F8:F11.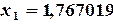 ;
; 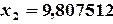 ;
; 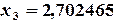 ;
; 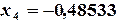
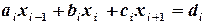
 , (2.6)
, (2.6)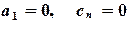 .
.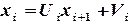 ,
,  (2.7)
(2.7)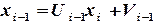 и подставим в (2.6):
и подставим в (2.6):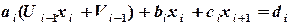
 :
: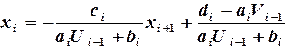 (2.8)
(2.8)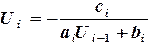
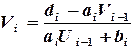
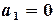 , то
, то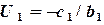 ,
, 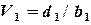 (2.10)
(2.10)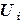 и
и 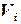 (
(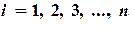 ). Это прямой ход прогонки. Зная прогоночные коэффициенты, по формулам (2.7), можно вычислить все
). Это прямой ход прогонки. Зная прогоночные коэффициенты, по формулам (2.7), можно вычислить все 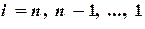 ) (обратный ход прогонки). Поскольку
) (обратный ход прогонки). Поскольку 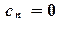 , то
, то  и
и 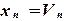 . Далее вычисляем
. Далее вычисляем  ,
, 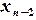 ,...,
,..., 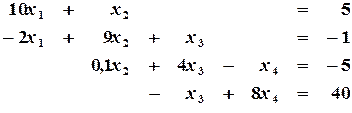
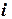
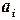
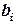
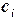
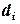
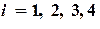 ).
).

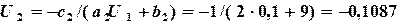
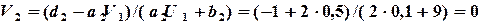
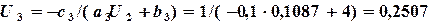
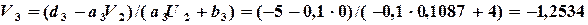
 , т.к.
, т.к. 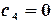
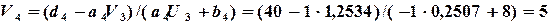
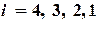 ). Поскольку
). Поскольку 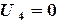 , то
, то 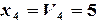 .
.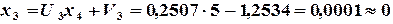

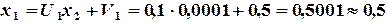
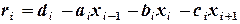 (
(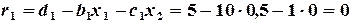

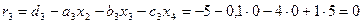
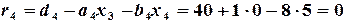
 (
(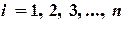 ).
). ).
).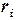 (
( =-C3/(A3*E2+B3)
=-C3/(A3*E2+B3)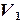 =(D3-A3*F2)/(A3*E2+B3)
=(D3-A3*F2)/(A3*E2+B3)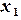 =(7-4*B2+C2)/7
=(7-4*B2+C2)/7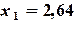 ,
, 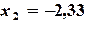 ,
, 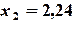
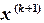 не используются до новой итерации. В методе Зейделя при нахождении
не используются до новой итерации. В методе Зейделя при нахождении 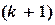 -ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой:
-ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой: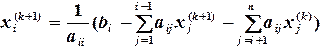 ,
, 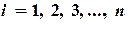 (2.17)
(2.17)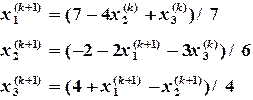
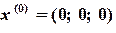 выражение для первой итерации имеет вид:
выражение для первой итерации имеет вид: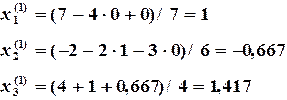
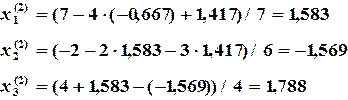
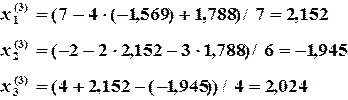
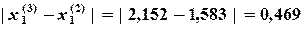
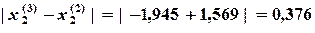
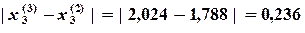
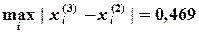
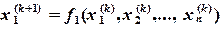

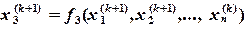 (3.6)
(3.6)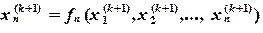
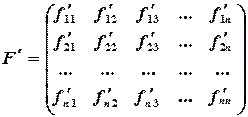 , (3.7)
, (3.7)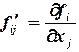 .
.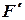 меньше единицы в некоторой окрестности корня:
меньше единицы в некоторой окрестности корня: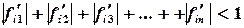 ,
, 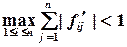
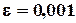 :
: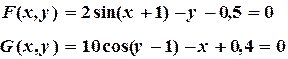 (3.8)
(3.8)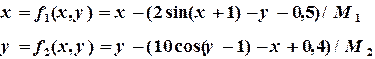 (3.9)
(3.9)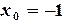 ,
, 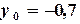 .
.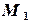 ,
, 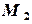 :
: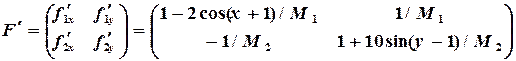

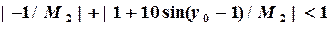
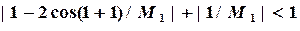
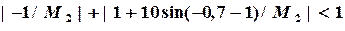
 и
и 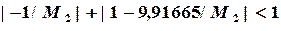
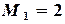 ,
, 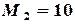 ,которые удовлетворяют неравенствам
,которые удовлетворяют неравенствам и
и 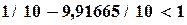
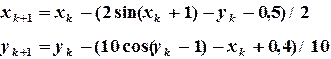

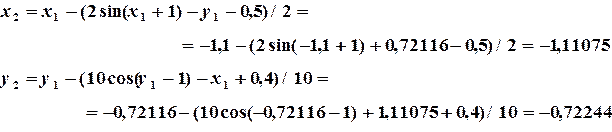
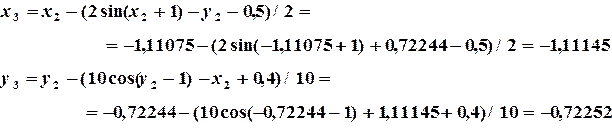
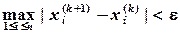 :
: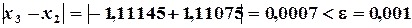
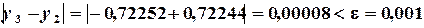
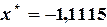 ,
, 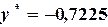 .
.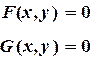 (3.10)
(3.10) ,
, 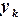 корня
корня 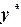 . Тогда поправки
. Тогда поправки 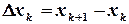 ,
, 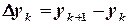 можно найти, решая систему:
можно найти, решая систему: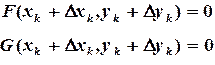 (3.11)
(3.11)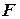 ,
, 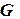 в ряд Тейлора по
в ряд Тейлора по 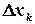 ,
, 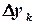 . Сохранив только линейные по
. Сохранив только линейные по 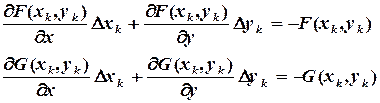 (3.12)
(3.12) (3.13)
(3.13) ;
; 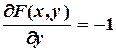


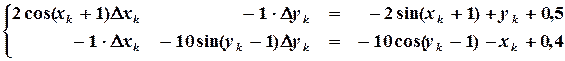
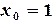 ,
, 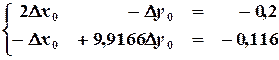 ,
,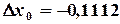 ,
, 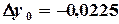

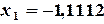 ,
,  и решая систему линейных уравнений
и решая систему линейных уравнений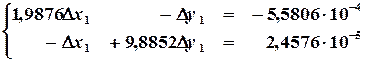 ,
,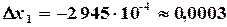 ,
, 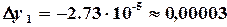
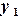 уточняем по формулам (3.12)
уточняем по формулам (3.12)