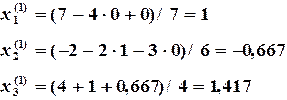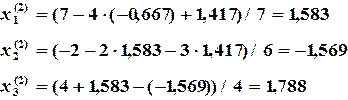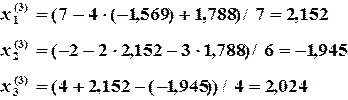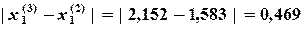Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод простой итерации (метод Якоби).Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Суть вычислений итерационными методами состоит в следующем: расчет начинается с некоторого заранее выбранного приближения
Затем процесс повторяется, только вместо
При выполнении некоторых заранее оговоренных условий процесс сходится при
Заданная точность достигается при выполнении условия:
Пример 2.5. Преобразовать систему уравнений:
к виду, пригодному для построения итерационного процесса методом Якоби и выполнить три итерации. Решение. Достаточное условие сходимости (2.13) выполняется, поэтому начальное приближение может быть любым.
В
Задается начальное приближение
Результаты первой итерации
Результаты второй итерации
Определяют достигнутую точность
Пример 2.6. Решить систему уравнений методом Якоби с помощью программы Excel с точностью
Порядок решения. 1) Представить систему в виде (2.16); 2) Ввести в ячейки A1:G1, D2:G2 заголовки столбцов (рис. 2.4); 3) В ячейки A2:C2 – начальное приближение 0, 0, 0; 4) В ячейку A3 – формулу 5) В ячейку B3 – формулу 6) В ячейку C3 – формулу 7) В ячейку D3 – формулу погрешности 8) Выделить ячейку D3 и скопировать формулу в соседние ячейки E3:F3 при помощи маркера заполнения; 9) В ячейку G3 – формулу максимальной погрешности =МАКС(D3:F3) 10) Выделить ячейки A3:G3 и скопировать формулы в соседние ячейки расположенных ниже строк A4:G4, A5:G5 и т.д.при помощи маркера заполнения. Каждая новая строка содержит результаты очередного приближения; 11) Ячейки A15, B15, C15 содержат решение системы уравнений, соответствующее заданной точности (G15).
Приближенное решение системы с точностью
Метод Зейделя. Вычисления в этом методе почти такие же, как и в методе Якоби, с той лишь разницей, что в последнем новые значения
Сходимость и точность достигаются условиями (2.13) и (2.14).
Пример 2.7. Задать итерационный процесс Зейделя для нахождения решений системы уравнений (2.15). Решение. Достаточное условие сходимости (2.13) выполняется, поэтому начальное приближение может быть любым. Используя (2.16) получим:
После задания начального приближения, например,
Результаты первой итерации подставляют в правую часть и получают результаты второй итерации:
Результаты второй итерации подставляют в правую часть и получают результаты третьей итерации:
Погрешность решения:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.22 (0.01 с.) |

 (начального приближения). Вычислительный процесс, использующий матрицу
(начального приближения). Вычислительный процесс, использующий матрицу 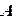 , вектор
, вектор 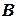 системы (2.1) и
системы (2.1) и  :
: ,
, 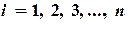 (2.11)
(2.11) -м шаге итерационного процесса по получают:
-м шаге итерационного процесса по получают: ,
,  . Сходимость метода простой итерации обеспечивается при выполнении условия преобладания диагональных элементов матрицы A, т.е. при:
. Сходимость метода простой итерации обеспечивается при выполнении условия преобладания диагональных элементов матрицы A, т.е. при: ,
, 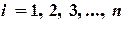 (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15)


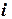 -ом уравнении все члены, кроме
-ом уравнении все члены, кроме  , переносятся в правую часть:
, переносятся в правую часть: (2.16)
(2.16) , которое подставляется в правую часть. Обычно
, которое подставляется в правую часть. Обычно  ,
,  ,
,  и получают результаты первой итерации:
и получают результаты первой итерации:
 подставляют в правую часть и получают результаты второй итерации:
подставляют в правую часть и получают результаты второй итерации:
 подставляют в правую часть и получают результаты третьей итерации:
подставляют в правую часть и получают результаты третьей итерации:
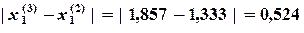



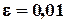 :
: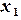 =(7-4*B2+C2)/7
=(7-4*B2+C2)/7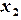 =(-2-2*A2-3*C2)/6
=(-2-2*A2-3*C2)/6 =(4+A2-B2)/4
=(4+A2-B2)/4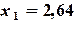 ,
, 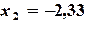 ,
, 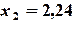
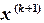 не используются до новой итерации. В методе Зейделя при нахождении
не используются до новой итерации. В методе Зейделя при нахождении 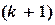 -ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой:
-ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой: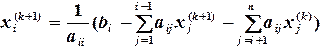 ,
, 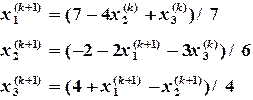
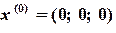 выражение для первой итерации имеет вид:
выражение для первой итерации имеет вид: