
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы решений алгебраических и трансцендентных уравненийСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ имени К.Г. РАЗУМОВСКОГО (Первый казачий университет)» (ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)») Башкирский институт технологий и управления (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный университет технологий и управления имени К.Г. Разумовского (Первый казачий университет)»БИТУ (филиал) ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)»
Вычислительная математика Учебное пособие для бакалавров Заочной формы обучения.
Предисловие
Вычислительная математика является одной из важнейших дисциплин профессиональной подготовки будущего инженера. Она развивает идеи численного решения задач, возникающих в процессе компьютерного математического моделирования реальных явлений в различных предметных сферах. Пособие включает краткие сведения по следующим разделам: основные понятия, связанные с приближенными значениями величин, методы оценки вычислительных ошибок; интерполирование функций; задачи численного интегрирования; методы численного решения обыкновенных дифференциальных уравнений. В каждом разделе приведены примеры выполнения индивидуальных заданий в «ручных» вычислениях. Задания могут выполняться и с помощью имеющихся в распоряжении студентов программно-технических средств – с помощью программ на каком-либо языке программирования или применения математических пакетов, которые в настоящее время широко используются в практических вычислениях: Exel, MatLab, MathCad, Maple и др. Рабочая программа Теория погрешностей Особенности математических вычислений, реализуемых на ЭВМ: представление чисел в форме с фиксированной и плавающей запятой, диапазон и погрешности представления, операции над числами, свойства арифметических операций. Абсолютная и относительная погрешности. Основные источники погрешности. Погрешность суммы, разности, произведения, частного. Погрешность функции. Обратная задача теории погрешностей.
Численные методы алгебры Действия с матрицами. вычисление определителей. обращение матриц. точные методы решения систем линейных алгебраических уравнений: правило Крамера, метод Гаусса, метод главных элементов. итерационные методы: метод итерации, метод Зейделя, метод релаксации. Численные методы решений алгебраических и трансцендентных уравнений Постановка задачи. Отделение корней. Графическое решение уравнений. Метод дихотомии, метод хорд, метод Ньютона, метод простой итерации. Приближенные методы решения систем нелинейных уравнений. Интерполяция и численное дифференцирование Постановка задачи интерполирования. Существование и единственность интерполяционного многочлена. Интерполяционный многочлен Лагранжа. Интерполяционные формулы Ньютона. Оценка погрешностей интерполяционных формул. Обратное интерполирование. Интерполяция сплайнами. Метод наименьших квадратов. Экстраполяция. Постановка задачи численного дифференцирования. Формулы приближенного дифференцирования, основанные на интерполяционных формулах. Численное интегрирование Постановка задачи численного интегрирования. Квадратурные формулы Ньютона-Котеса. Квадратурные формулы Гаусса. Численные методы решения обыкновенных дифференциальных уравнений Постановка задачи. Решение задачи Коши с помощью формулы Тейлора. Метод Эйлера. Метод Рунге-Кутта. Многошаговые методы. Понятие о численных методах решения дифференциальных уравнений частных производных. Теория погрешностей
Интерполирование функций
Квадратурная формула Гаусса Если вычисляется интеграл
где tj и Dj находятся из таблицы.
Остаточный член формулы Гаусса (7) выражается формулой
Пример 11. Вычислить интеграл Решение. Для достижения заданной степени точности необходимо определить значение n так, чтобы
Здесь Находим
Положим М2 =7, тогда неравенство примет вид
Вычисление интеграла производим по формуле
где
Все расчеты приведены в таблице.
Таким образом,
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ имени К.Г. РАЗУМОВСКОГО (Первый казачий университет)» (ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)») Башкирский институт технологий и управления (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный университет технологий и управления имени К.Г. Разумовского (Первый казачий университет)»БИТУ (филиал) ФГБОУ ВО «МГУТУ им. К.Г. Разумовского (ПКУ)»
Вычислительная математика Учебное пособие для бакалавров Заочной формы обучения.
Предисловие
Вычислительная математика является одной из важнейших дисциплин профессиональной подготовки будущего инженера. Она развивает идеи численного решения задач, возникающих в процессе компьютерного математического моделирования реальных явлений в различных предметных сферах. Пособие включает краткие сведения по следующим разделам: основные понятия, связанные с приближенными значениями величин, методы оценки вычислительных ошибок; интерполирование функций; задачи численного интегрирования; методы численного решения обыкновенных дифференциальных уравнений. В каждом разделе приведены примеры выполнения индивидуальных заданий в «ручных» вычислениях. Задания могут выполняться и с помощью имеющихся в распоряжении студентов программно-технических средств – с помощью программ на каком-либо языке программирования или применения математических пакетов, которые в настоящее время широко используются в практических вычислениях: Exel, MatLab, MathCad, Maple и др. Рабочая программа Теория погрешностей Особенности математических вычислений, реализуемых на ЭВМ: представление чисел в форме с фиксированной и плавающей запятой, диапазон и погрешности представления, операции над числами, свойства арифметических операций. Абсолютная и относительная погрешности. Основные источники погрешности. Погрешность суммы, разности, произведения, частного. Погрешность функции. Обратная задача теории погрешностей. Численные методы алгебры Действия с матрицами. вычисление определителей. обращение матриц. точные методы решения систем линейных алгебраических уравнений: правило Крамера, метод Гаусса, метод главных элементов. итерационные методы: метод итерации, метод Зейделя, метод релаксации.
Численные методы решений алгебраических и трансцендентных уравнений Постановка задачи. Отделение корней. Графическое решение уравнений. Метод дихотомии, метод хорд, метод Ньютона, метод простой итерации. Приближенные методы решения систем нелинейных уравнений.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.15.129 (0.01 с.) |

 , то с помощью линейной замены
, то с помощью линейной замены  получим
получим

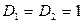



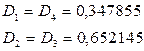

 по формуле трапеций с тремя десятичными знаками.
по формуле трапеций с тремя десятичными знаками. .
. , где
, где  .
. ;
; 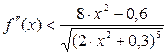 ;
; .
. , откуда
, откуда  , т.е.
, т.е. 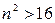 ; возьмем
; возьмем  .
. ,
,






 .
.


