
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратурные формулы Ньютона-КотесаСодержание книги Поиск на нашем сайте
Наиболее широко для вычисления определенных интегралов используются приближенные равенства вида
Здесь xj Î [ a, b ] –узлы квадратурной формулы; Dj – числовые коэффициенты, называемые весами квадратурной формулы; n – натуральное число. Величина
Называется погрешностью квадратурной формулы. Будем говорить, что квадратурная формула (14) точна для многочленов степени m, если для любого многочлена степени не выше m эта формула дает точное значение интеграла, т.е.
(m – порядок точности квадратуры). Многие квадратурные формулы основаны на замене подынтегральной функции на более простую функцию, близкую к f(x), легко интегрируемую точно. В качестве такой функции берут либо алгебраический многочлен, либо рациональную функцию, тригонометрический многочлен и т.д. Рассмотрим квадратурные формулы, получаемые с помощью интегрирования интерполяционного многочлена и объединенных одним общим названием – формулы Ньютона-Котеса. Рассмотрим вычисление интегралов вида Для случая p(x) º 1 приведем ряд простейших квадратурных формул. 1. Формула прямоугольников.
Погрешность метода 2. Формула трапеций.
Погрешность метода 3. Формула Симпсона.
Погрешность метода Во многих случаях оценка погрешности квадратурных формул по приведенным оценкам затруднительна. Тогда обычно проводят двойной подсчет с шагами h и 2h и считают, что совпадающие десятичные знаки принадлежат точному значению интеграла. Можно указать практический способ подсчета ошибки квадратурной формулы. Пусть Sh и S2h – приближенные значения интеграла I, полученные с шагами h и 2h. Тогда, примерно, I = Sh + Ch4 (считая, что y(IV)(x) на отрезке меняется медленно, тогда погрешность R ~ Ch4). I = S2h + C(2h)4 = S2h + 16Ch4. Sh - S2h =15Ch4; Ch4 = (Sh - S2h)/15. Тогда за приближенное значение интеграла целесообразно принять значение, определяемое выражением:
В случае квадратурных формул с равноотстоящими узлами их точность в основном характеризуется порядком остаточного члена R = o(hm), где Для формулы трапеций m = 2, Симпсона – m = 4. Квадратурная формула считается тем точнее, чем выше (для больших степеней при стремлении шага интегрирования к нулю погрешность стремится к нулю быстрее). Естественно, эта закономерность проявляется при достаточно большом числе M.
Квадратурная формула Гаусса Если вычисляется интеграл
где tj и Dj находятся из таблицы.
Остаточный член формулы Гаусса (7) выражается формулой
Пример 11. Вычислить интеграл Решение. Для достижения заданной степени точности необходимо определить значение n так, чтобы
Здесь Находим
Положим М2 =7, тогда неравенство примет вид Вычисление интеграла производим по формуле
где
Все расчеты приведены в таблице.
Таким образом,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.008 с.) |

 .
.
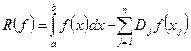 .
.
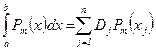 .
. , где f(x) – хорошо приближается многочленом, p(x) – некоторая фиксированная функция, называемая весовой функцией или весом и учитывающая особенности подынтегральной функции.
, где f(x) – хорошо приближается многочленом, p(x) – некоторая фиксированная функция, называемая весовой функцией или весом и учитывающая особенности подынтегральной функции. .
.
 .
.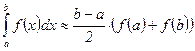 .
.
 .
. .
.
 .
. .
. – шаг интегрирования.
– шаг интегрирования. , то с помощью линейной замены
, то с помощью линейной замены  получим
получим

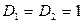



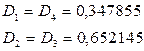

 по формуле трапеций с тремя десятичными знаками.
по формуле трапеций с тремя десятичными знаками. .
. , где
, где  .
. ;
; 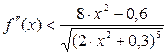 ;
; .
. , откуда
, откуда  , т.е.
, т.е. 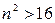 ; возьмем
; возьмем  .
. ,
,






 .
.


