Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы решения обыкновенных дифференциальных уравнений ⇐ ПредыдущаяСтр 5 из 5
Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка
Задача Коши: Найти решение уравнения (20) y = y (x), удовлетворяющее начальному условию y (x0) = y0. Геометрически это означает, что требуется найти интегральную кривую Существует несколько классов дифференциальных уравнений первого порядка, для которых решение может быть найдено аналитически (уравнение с разделяющимися переменными, однородные, линейные, в полных дифференциалах). Даже для таких уравнений решение не всегда удается довести до вида Многие же дифференциальные уравнения, к которым приводят математические модели реальных процессов, не относятся к указанным классам и аналитически решены быть не могут. Тем более это утверждение справедливо для систем дифференциальных уравнений и для уравнений старших порядков. По этой причине разработаны многочисленные методы приближенного решения дифференциальных уравнений. Весьма условно, в зависимости от формы предоставления решения, эти методы подразделяются на три основные группы: –аналитические методы, применение которых дает приближенное решение дифференциальных уравнений в виде формулы; –графические методы, делящие приближенное решение в виде графика; –численные методы, когда искомая функция получается в виде таблицы.
Метод Эйлера Метод Эйлера – простейший представитель пошаговых методов. Получение таблицы значений искомой функции
Отметим, что оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага, исходное значение Наиболее используемым эмпирическим методом оценки точности как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка – с шагом h и с шагом
Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает эмпирическое обоснование считать их верными. Пример 12. Решить методом Эйлера дифференциальное уравнение Решение. Результаты вычислений с двумя знаками после запятой приведены в таблице.
Порядок вычислений вполне очевиден: вначале находим
Сопоставление приближений, полученных с различным шагом, показывает, что при выбранном шаге метод Эйлера дает невысокую точность – в пределах одной-двух значащих цифр.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.13 (0.005 с.) |

 , проходящую через заданную точку
, проходящую через заданную точку  .
. – функция, с которой удобно работать дальше.
– функция, с которой удобно работать дальше. . (21)
. (21) само является приближенным, т.е. вообще говоря, погрешность на каждом следующем шаге систематически возрастает.
само является приближенным, т.е. вообще говоря, погрешность на каждом следующем шаге систематически возрастает. .
. с начальным условием
с начальным условием  на отрезке
на отрезке  , приняв шаг
, приняв шаг  .
.
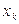


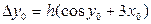 , затем
, затем  и т.д. Если шаг уменьшить вдвое (т.е.
и т.д. Если шаг уменьшить вдвое (т.е.  ), то получим следующие значения
), то получим следующие значения