
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Десятичная запись и округление приближенных чиселСодержание книги Поиск на нашем сайте На практике преимущественно приходится иметь дело с приближенными числами, представляющие собой конечные десятичные дроби. Любое десятичное число представимо в виде
Значащими цифрами числа b называют все цифры в его записи, начиная с первой ненулевой слева (bm). В числе (4) n = m + k + 1 значащих цифр. Пример 2. a = 0,0 3045 –4 значащих цифры; a = 0,0 3045000 –7 значащих цифр. Значащую цифру называют верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре. Пример 3. a = 0,0 3045 – Da = 0,000005; a = 0,0 30450 00 – Da = 0,0000005. Если все значащие цифры верны, то говорят, что число записано со всеми верными цифрами. Подчеркнем, что числа, помещенные в математических таблицах, имеют все верные цифры. Сомнительными называют все цифры приближенного числа, расположенные правее последней верной цифры. Заметим, что обычно пишут знак равенства между точными и приближенными числами, если все цифры приближенного числа верные. В процессе вычислений часто происходит округление чисел, т.е. замена чисел их значениями с меньшим количеством значащих цифр. При округлении возникает погрешность, называемая погрешностью округления. Пусть х – данное число, а х 1 – результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:
Погрешность округления следует прибавить к первоначальной абсолютной погрешности приближенного числа. Для того, чтобы погрешность округления была минимальной, пользуются следующими правилами: 1. если первая отбрасываемая цифра меньше 5, то последняя сохраняемая цифра не изменяется; 2. если первая отбрасываемая цифра равна или больше 5, то последняя сохраняемая цифра увеличивается на единицу; 3. если отбрасывается одна цифра 5, то последняя сохраняемая цифра не изменяется, если она четная, и увеличивается на единицу, если она нечетная. Пример 4. Приближенное число а =16,8314 с абсолютной погрешностью Решение. Так как Абсолютная погрешность округленного числа 0,0032+0,0014=0,0046. Выполнив округление погрешности в сторону увеличения, получим новую погрешность, равную 0,005. Пример 5. Определить, какое равенство точнее: 9/11=0,818 или Решение. Находим значения данных выражений с большим числом десятичных знаков:
Предельные относительные погрешности составляют:
Так как
|
||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 округлить до его верных цифр и найти абсолютную погрешность округленного числа.
округлить до его верных цифр и найти абсолютную погрешность округленного числа. , то цифра сотых (3) – верная, а следовательно, верны и предшествующие цифры 1, 6 и 8. Таким образом, округленное число
, то цифра сотых (3) – верная, а следовательно, верны и предшествующие цифры 1, 6 и 8. Таким образом, округленное число  имеет все верные цифры.
имеет все верные цифры.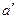 равна сумме первоначальной погрешности 0,0032 и погрешности округления (0,0014):
равна сумме первоначальной погрешности 0,0032 и погрешности округления (0,0014):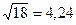 .
. . Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:
. Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:
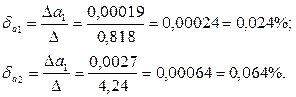
 , то равенство 9/11=0,818 является более точным.
, то равенство 9/11=0,818 является более точным.


