
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи интерполированияСодержание книги Поиск на нашем сайте
Простейшая задача интерполирования заключается в следующем. На отрезке [ a, b ] заданы n + 1 точки x0, x1, …, xn, которые называются узлами интерполяции, в которых некоторая функция f(x) принимает значения
Требуется построить функцию F(x) (интерполяционную функцию) принадлежащую известному классу функций и принимающую в узлах интерполяции те же значения, что и f(x), т.е. такую, что
Геометрически это означает, что нужно найти кривую y = F(x) некоторого определенного типа, проходящую через заданную систему точек Mi(xi, yi), i = 0, 1, 2, …, n. В такой общей постановке задача может иметь бесчисленное множество решений или совсем не иметь решений. Однако эта задача становится однозначной, если вместо произвольной функции F(x) искать полином Pn(x) – степени не выше n, удовлетворяющий условиям (9), т.е. такой, что Pn(x0) = y0, Pn(x1) = y1, …, Pn(xn) = yn. Полученную интерполяционную формулу y = F(x) обычно используют для приближенного вычисления значений данной функции f(x) для значений аргумента x, отличных от узлов интерполирования. Такая операция называется интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда x Î [ x0, xn ], т.е. значение x является промежуточным между x0 и xn и экстраполирование, когда x Ï [ x0, xn ].
Интерполяционная формула Лагранжа Пусть на отрезке [ a, b ] задан n + 1 узел интерполяции x0, x1, …, xn в которых заданы значения функции yi = f(xi), i = 0, 1, …, n. Требуется построить полином Ln(x) степени не выше n, принимающий в данных узлах те же значения, что и указанная функция. Интерполяционная формула Лагранжа имеет вид
Пример 9. Построить интерполяционный многочлен Лагранжа для функции, заданной таблицей значений:
Решение. Из таблицы следует, что n =2 (т.е. степень многочлена будет не выше 2); здесь х 0=1, х 1=3, х 2=4.
Если обозначить произведение
по формуле Лагранжа можно придать более сжатый вид
В случае равноотстоящих узлов интерполяционная формула Лагранжа принимает вид
где Для оценки погрешности интерполяционной формулы Лагранжа можно использовать соотношение
где Рассмотрим частные случаи формулы Лагранжа. При n = 1 имеем две точки и формула Лагранжа – уравнение прямой проходящей через эти точки.
При n = 2 – уравнение параболы проходящей через три точки.
Пример 10. Найти приближенное значения функции у(х) при х =0,1157 с помощью интерполяционного многочлена Лагранжа, если функция задана в равноотстоящих узлах таблицы.
Решение. Для вычислений используем формулу
где Здесь t =(0,1157-0,101)/0,005=2,94. Вычисления располагаем в таблице.
Итак, Следовательно,
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.24 (0.005 с.) |

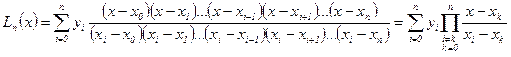 (10)
(10)
 ,
, ,
, . (11)
. (11) , (12)
, (12) .
. ,
, зависит от
зависит от 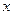 и
и  .
. .
.
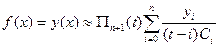 ,
, .
.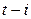
 Ci
Ci


 .
.


