
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы решения систем нелинейных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Требуется решить систему нелинейных уравнений вида:
…
Метод простой итерации (метод Якоби). Систему нелинейных уравнений (3.1) после преобразований
(здесь
…
Из системы (3.2) легко получить итерационные формулы метода Якоби. Возьмем в качестве начального приближения какую-нибудь совокупность чисел
…
Эта операция получения первого приближения
Итерационный процесс можно считать законченным, если все значения переменных, полученных (
Метод Зейделя. Метод Зейделя отличается от метода Якоби тем, что вычисления ведутся не по формулам (3.4), а по следующим формулам:
…
При решении систем нелинейных уравнений необходимо определить приемлемое начальное приближение. Для случая двух уравнений с двумя неизвестными начальное приближение находится графически. Сходимость метода Зейделя (Якоби тоже) зависит от вида функции в (3.2), вернее она зависит от матрицы, составленной из частных производных:
где Итерационный процесс сходится, если сумма модулей каждой строки
или Пример 3.1. Найти решение системы методом Зейделя с точностью
Решение: Представим (3.8) в виде (3.5):
Задаем начальные приближения Запишем достаточное условие сходимости и определяем
Определяем частныезначения
Переходим к реализации итерационного процесса:
Определяем погрешностьпо формуле
Таким образом, имеем решение: Программа, реализующая решение данной задачи, представлена на рис. 3.1.
Метод Ньютона. Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности систем линейных уравнений. Рассмотрим систему двух нелинейных уравнений с двумя неизвестными вида:
Пусть известно некоторое приближение
Для этого разложим функции
относительно неизвестных поправок Таким образом, решение системы уравнений по методу Ньютона состоит в построении итерационной последовательности:
где В методе Ньютона для обеспечения хорошей сходимости также важен правильный выбор начального приближения. Пример 3.2. Найти решение системы (3.8) методом Ньютона с точностью
Решение. Начальные приближения
и, используя (3.12), построим систему линейных уравнений относительно поправок
Подставляя начальные приближения
определяем поправки на первом шаге итерации
Далее начальное приближение уточняем по формулам (3.13)
Подставляя результаты первой итерации
определяем поправки на втором шаге итерации
Далее
Определяем погрешностьпо формуле
Таким образом, имеем решение: Программа, реализующая метод Ньютона для указанной задачи, представлена на рис. 3.2.
Пример 3.3. Найти решение системы (3.8) с помощью программы Excel.
Порядок решения. 1) Подключить надстройку «Поиск решения» через Главное меню-Сервис-Надстройки (рис. 3.3); 2) Ввести в ячейки A1, B1, C1, D1 заголовки столбцов (рис. 3.4а);
3) В ячейку A2 – начальное приближение для 4) В ячейку B2 – начальное приближение для 5) В ячейку C2 – формулу 6) В ячейку D2 – формулу 7) Вызвать диалоговое окно «Поиск решения»: Главное меню-Сервис-Поиск решения (рис. 3.5) 8) В качестве целевой ячейки указываем результат вычисления левой части одного из уравнений, например, 9) Для решения уравнения значение 10) Установив курсор в поле «Изменяя ячейки», выделяем ячейки незвестных 11) Остальные уравнения системы рассматриваются как дополнительные ограничения ( 12) Нажимаем кнопку «Выполнить». Если решение найдено, появляется окно сообщения (рис. 3.6). Нажимаем кнопку ОК. 13) В ячейках A2: B2 - решение системы (рис. 3.4б), т.е
ЛИТЕРАТУРА 1. Калиткин Н.П. Численные методы. М.: Наука, 1978. - 512 с. 2. Турчак Л.И., Плотников П.В. Основы численных методов: Учебное пособие. М.: ФИЗМАТЛИТ, 2003. – 304 с. 3. Васильев А.Н. Научные вычисления в Microsoft Excel. М.: Издательский дом "Вильямс", 2004. – 512 с. 4. Ларсен У.Р. Инженерные расчеты в Excel. М.: Издательский дом "Вильямс", 2004. – 544 с. 5. Попов В.И. Численные методы расчета мостовых конструкций на ЭВМ. М.: 1981. – 78 с. 6. Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. Методические указания к лабораторным работам по курсу «Информатика» для всех специальностей. Численные методы. Часть 1. КГАСУ, 2008г., 34с. 7. Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. Методические указания к лабораторным работам по курсу «Информатика» для всех специальностей. Численные методы. Часть 2. КГАСУ, 2008г., 35с.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.73.98 (0.007 с.) |


 (3.1)
(3.1)
 ,
, 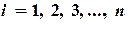
 определяются из условия сходимости), представим в виде:
определяются из условия сходимости), представим в виде:
 (3.2)
(3.2)
 . Подставляя их в правую часть (3.2) вместо переменных
. Подставляя их в правую часть (3.2) вместо переменных 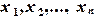 , получим новое приближение к решению исходной системы:
, получим новое приближение к решению исходной системы:
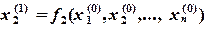 (3.3)
(3.3)
 решения системы уравнения (3.2) называется первым шагом итерации. Подставляя полученное решение в правую часть уравнения (3.2) получим следующее итерационное приближение:
решения системы уравнения (3.2) называется первым шагом итерации. Подставляя полученное решение в правую часть уравнения (3.2) получим следующее итерационное приближение:  и т.д.:
и т.д.: ,
,  )-ой итерации, отличается от значений соответствующих переменных, полученных от предыдущей итерации, по модулю меньше наперед заданной точности
)-ой итерации, отличается от значений соответствующих переменных, полученных от предыдущей итерации, по модулю меньше наперед заданной точности 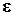 , т.е. если:
, т.е. если: (3.5)
(3.5)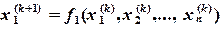

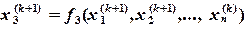 (3.6)
(3.6)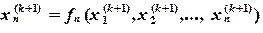
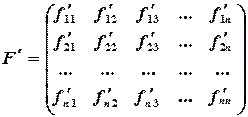 , (3.7)
, (3.7)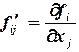 .
.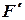 меньше единицы в некоторой окрестности корня:
меньше единицы в некоторой окрестности корня: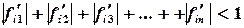 ,
, 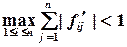
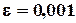 :
: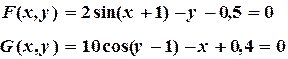 (3.8)
(3.8)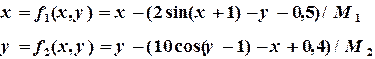 (3.9)
(3.9)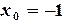 ,
, 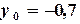 .
.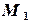 ,
, 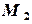 :
: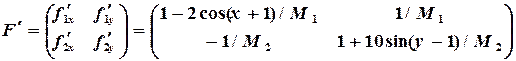

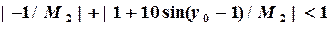
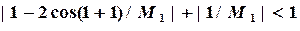
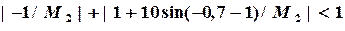
 и
и 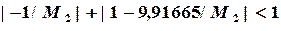
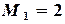 ,
, 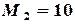 ,которые удовлетворяют неравенствам
,которые удовлетворяют неравенствам и
и 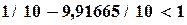
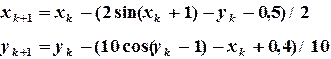

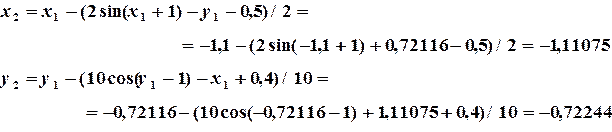
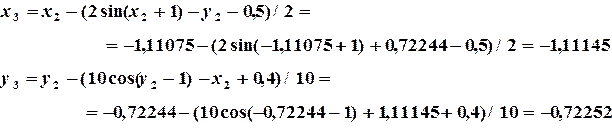
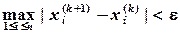 :
: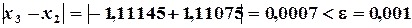
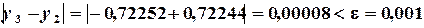
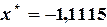 ,
, 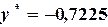 .
.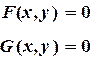 (3.10)
(3.10) ,
, 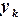 корня
корня 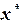 ,
, 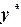 . Тогда поправки
. Тогда поправки 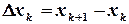 ,
, 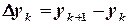 можно найти, решая систему:
можно найти, решая систему: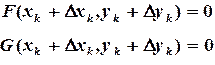 (3.11)
(3.11)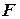 ,
, 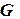 в ряд Тейлора по
в ряд Тейлора по 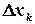 ,
, 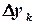 . Сохранив только линейные по
. Сохранив только линейные по 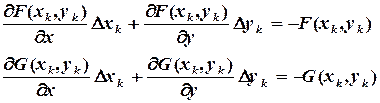 (3.12)
(3.12) (3.13)
(3.13) ;
; 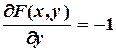


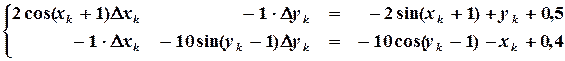
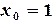 ,
, 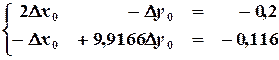 ,
,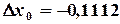 ,
, 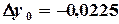

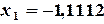 ,
,  и решая систему линейных уравнений
и решая систему линейных уравнений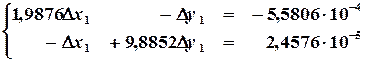 ,
,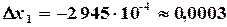 ,
, 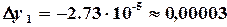
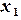 и
и 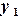 уточняем по формулам (3.12)
уточняем по формулам (3.12)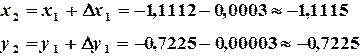
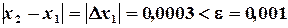
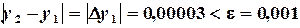
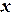 :
: 
 :
: 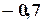
 =2*SIN(A2+1)-B2-0,5
=2*SIN(A2+1)-B2-0,5 =10*COS(B2-1)-A2+0,4
=10*COS(B2-1)-A2+0,4 , поэтому выбираем переключатель «значение», а в соответствующее поле вводим 0
, поэтому выбираем переключатель «значение», а в соответствующее поле вводим 0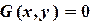 ). Нажимаем кнопку «Добавить», отмечаем мышью ячейку D2 и вводим =0
). Нажимаем кнопку «Добавить», отмечаем мышью ячейку D2 и вводим =0 ,
, 

 б)
б) 





