Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение дифференциальных уравнений и системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нелинейные дифференциальные уравнения и системы с такими уравнениями, как правило, не имеют аналитических методов решения, и здесь особенно важна возможность из решения численными методами. В большинстве случаев желательно представление решений в графическом виде, что также позволяет MathCad. Для решения задач такого класса можно использовать ряд функций: Odesolve(x,b,[step]) - возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given. x - переменная интегрирования, действительное число b - конечная точка отрезка интегрирования step - величина шага по переменной интегрирования (необязательный аргумент) Rkadapt(y,x1,x2,n,F) - возвращает матрицу решений методом Рунге-Кутта с переменным шагом для системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F, на интервале от x1 до x2 при фиксированном числе шагов n; rkfixed(y,x1,x2,n,F) - возвращает матрицу решений методом Рунге-Кутта системы обыкновенных дифференциальных уравнений с начальными условиями в векторе y, правые части которых записаны в символьном векторе F, на интервале от x1 до x2 при фиксированном числе шагов n. Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и является его заключительным ключевым словом. Пример использования функции приведен на рис.68.
Рис.68. Пример решения дифференциального уравнения второго порядка с помощью функции Odesolve.
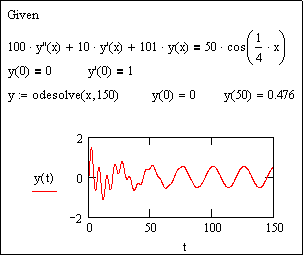
Системы линейных дифференциальных уравнений первого порядка решаются с помощью функции Rkfixed. На рис.2 приведен пример применения функции rkfixed для решения дифференциального уравнения, описывающего процесс свободных затухающих колебаний величины электрического заряда q (К) на конденсаторе с емкостью С (Ф), включенного в замкнутый контур, содержащий также сопротивление R (Ом) и индуктивность L (Гн). Этот процесс описывается дифференциальным уравнением второго порядка
где
b – коэффициент затухания, 1/с, wc– круговая частота собственных колебаний контура, 1/с, Исходные данные к решению задачи: Начальное условие: t=0, Vq=0, q=q0.
Процесс затухания колебаний рассчитать до tk Исходное дифференциальное уравнение второго порядка может быть преобразовано в систему дифференциальных уравнений первого порядка. Для этого введем подстановки: q0=q q1= Дифференциальное уравнение второго порядка преобразуем в систему дифференциальных уравнений первого порядка:
Правые части системы дифференциальных уравнений записываются в вектор правых частей системы уравнений D(t,q). Матрица Z размерности n строк по числу точек вывода результатов решения и m+1 столбцов, равным числу уравнений в системе. В столбцах матрицы содержатся значения переменных соответственно t,
Рис.69. Пример решения дифференциального уравнения второго порядка с помощью функции rkfixed. Оборудование, инструменты и приборы ПЭВМ, система MathCad Варианты заданий Варианты заданий приведены в таблицах 4.16 -4.17. Задание 1 Найти частное решение y(x) дифференциального уравнения для своего варианта при произвольных начальных условиях и построить график решения. Варианты заданий приведены в табл.4.16.
Таблица 4.16 Варианты заданий
Задание 2 Решите систему дифференциальных уравнений для своего варианта на отрезке [0,3]. Выведите значения искомых функций и их производных в точке с координатой х=1.5. Варианты заданий приведены в табл.4.17.
Таблица 4.17 Варианты заданий
Задание 3
Решить задачу, рассмотренную в пункте 8 с учетом данных своего варианта. Для вариантов 1 – 5: tk=45с, для вариантов 6 – 10: tk=40с, для вариантов 11 – 15: tk=50с, для вариантов 16 – 20: tk=55с, для вариантов 21 – 25: tk=35с, для вариантов 26 – 30: tk=30с.
Порядок выполнения работы. 1. Создать MathCad – документ и сохранить его под именем «Решение_дифф_уравнений_систем». 2. Выполнить задания в соответствии с данными своего варианта. Содержание отчета. В отчете по лабораторной работе должно быть дано описание методов решения дифференциальных уравнений и систем. В отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “ Решение_ дифф_уравнений_систем ”.
Контрольные вопросы. 1. При помощи каких функций решаются нелинейные дифференциальные уравнения? 2. При помощи каких функций решаются системы дифференциальных уравнений? 3. Решить дифференциальное уравнение по заданию преподавателя. 4. Решить систему дифференциальных уравнений по заданию преподавателя.
Лабораторная работа № 25
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |



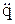 =d2q/dt2 – ускорение изменения заряда, К/с2;
=d2q/dt2 – ускорение изменения заряда, К/с2; =dq/dt – скорость изменения заряда, К/с;
=dq/dt – скорость изменения заряда, К/с; ;
;
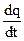

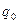 ,
, 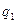 . На рис.2 представлен график изменения заряда от времени.
. На рис.2 представлен график изменения заряда от времени.